蓝桥杯-路径之谜

问题描述
小明冒充 X 星球的骑士，进入了一个奇怪的城堡，城堡里边什么都没有，只有方形石头铺成的地面。

假设城堡地面是 n x n 个方格，如图所示。

 

 

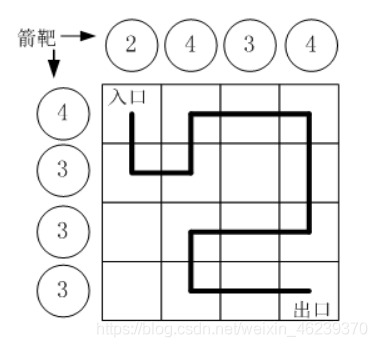
按习俗，骑士要从西北角走到东南角，可以横向或纵向移动，但不能斜着走，也不能跳跃。

每走到一个新方格，就要向正北方和正西方各射一箭。（城堡的西墙和北墙内各有 n 个靶子）

同一个方格只允许经过一次，但不必走完所有的方格。

如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？有时是可以的，比如图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入格式
第一行一个整数 N，表示地面有 N x N 个方格 (0 < N < 20)
第二行 N 个整数，空格分开，表示北边的箭靶上的数字（自西向东）
第三行 N 个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出格式
一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号: 0, 1, 2, 3…
比如，图中的方块编号为：

0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

样例输入
4
2 4 3 4
4 3 3 3

样例输出
0 4 5 1 2 3 7 11 10 9 13 14 15
这题可以使用dfs进行解决

#include <iostream>
using namespace std;

const int N = 22;
int col[N];
int row[N];
int g[N][N];
int ans[1000];
int count = 0;
int n;
//判断col和row是否被清空
bool check()
{
  for(int i = 0;i < n;i++)
  {
    if (col[i] != 0 || row[i] != 0)
    {
      return false;
    }
  }
  return true;
}
int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1};
void dfs(int x,int y)
{
　 //走到终点，并且col和row数组满足要求，救输出结果
  if (x == n - 1 && y == n - 1)
  {
    if (check())
    {
      for(int i = 0;i <count;i++)
      {
        cout << ans[i] << " ";
      }
    }
  }
  //dfs搜索
  int tx,ty;
  for(int i = 0;i < 4;i++)
  {
    tx = x + dx[i];
    ty = y + dy[i];
    if (tx >= 0 && tx < n && ty >= 0 && ty < n && g[tx][ty] == 0 && col[ty] && row[tx])
    {
      g[tx][ty] = 1;
      col[ty]--;
      row[tx]--;
      ans[count++] = n * tx + ty;
      dfs(tx,ty);
      col[ty]++;
      row[tx]++;
      g[tx][ty] = 0;
      count--;
    }
  }
}
int main()
{
  cin >> n;
  for(int i = 0;i < n;i++)
  {
    cin >> col[i];
  }
  for(int i = 0;i < n;i++)
  {
    cin >> row[i];
  }
  //从(0,0)触发,此点已被访问
  g[0][0] = 1;
  ans[count++] = 0;
  col[0]--;
  row[0]--;
  dfs(0,0);
  return 0;
}