bfs走迷宫

广度优先搜索（也称宽度优先搜索，缩写BFS，以下采用广度来描述）是连通图的一种遍历算法这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。基本过程，BFS是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。一般用队列数据结构来辅助实现BFS算法。

 

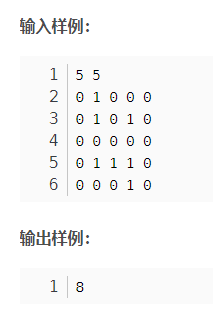
来看一个例子

一、题目描述

给定一个 n × m 的二维整数数组，用来表示一个迷宫，数组中只包含 0或 1，其中 0表示可以走的路，1表示不可通过的墙壁。

最初，有一个人位于左上角 ( 1 , 1 )处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 ( n , m )处，至少需要移动多少次。

数据保证 ( 1 , 1 ) 处和 ( n , m ) )处的数字为 0 ，且一定至少存在一条通路。

输入格式

第一行包含两个整数 n 和 m 。

接下来 n 行，每行包含 m 个整数（0 或 1 ），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1 ≤ n , m ≤ 100

 

 

#include <iostream>
#include<stdio.h>
#include<algorithm>
#include <queue>
#include<cstring>
using namespace std;
const int N = 1002;
//用于存储坐标
typedef pair<int,int> PII;
queue<int> stk;
int d[N][N];
char g[N][N];
int n,m,st_x,st_y,end_x,end_y;

void bfs()
{
    queue<PII> q;
    memset(d,-1,sizeof(d));
    
    //设置起点
    d[st_x-1][st_y-1] = 0;
    q.push({st_x-1,st_y-1});

    //四种可能的走法
    int dx[4] = {-1,0,1,0};
    int dy[4] = {0,1,0,-1};
    while (q.size())
    { 
        //取出一个点
        auto t = q.front();
        q.pop();
        //判断这个点周围是否存在可走的点,有就加入到数组
        for(int i = 0;i < 4;i++)
        {
            int x = t.first + dx[i],y = t.second + dy[i];
            if (x >=0 && x < n && y >=0 && y < n && g[x][y] == '.' && d[x][y] == -1)
            {
                //设置该点距离起点的距离
                d[x][y] = d[t.first][t.second] + 1;
                //把这个点入队
                q.push({x,y});
            }
        }
    }
    //未能到达这个点
    if (d[end_x - 1][end_y - 1] == -1)
    {
        cout << "-1" << endl;
    }
    else
    {
        cout << d[end_x - 1][end_y - 1];
    }
}
int main() {
    cin >> n >> m;
    cin >> st_x >> st_y >> end_x >> end_y;
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < m;j++)
        {
            cin >> g[i][j];
        }
    }
    
    bfs();
    return 0;
}