拓扑排序

拓扑排序是一种图论算法，它用于对有向无环图（DAG）进行排序。该算法的目的是找到图中所有顶点的线性排列，使得对于图中的任意两个顶点 u 和 v，如果存在一条从 u 到 v 的边，那么在排列中 v 出现在 u 的后面。

拓扑排序的解决思路为

1.从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出

2.从图中删除该顶点和所有以它为起点的有向边

3.重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

 

 

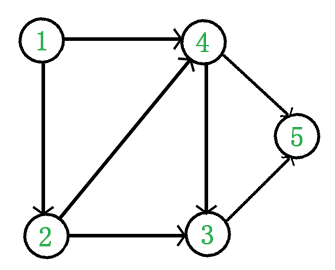
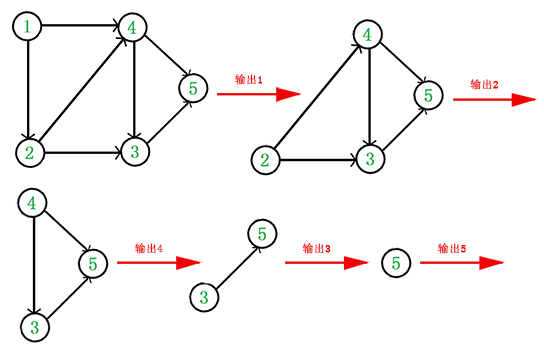
 得到的拓扑顺序为{1,2,4,3,5}

描述

给定一个包含n个点m条边的有向无环图，求出该图的拓扑序。若图的拓扑序不唯一，输出任意合法的拓扑序即可。若该图不能拓扑排序，输出-1。

输入描述：

第一行输入两个整数n,m，表示点的个数和边的条数。
接下来的m行，每行输入两个整数ui,vi,表示ui​到vi​之间有一条有向边。

输出描述：

若图存在拓扑序，输出一行n个整数，表示拓扑序。否则输出-1。

#include <iostream>
#include<stdio.h>
#include<list>
#include <vector>
#include <queue>
using namespace std;
//使用嵌套vector表示邻接表
vector<list<int>> adj;
vector<int> inDegree;
queue<int> stk;
int n;
int m;
//创建拓扑图,使用邻接表
void CreateGraph()
{    
    cin >> n >> m;
    //对邻接表和入度表初始化
    adj.assign(n+1,list<int>());
    inDegree.assign(n+1,0);
    int in,out;
    while (m--)
    {
        cin >> in >> out;
        adj[in].push_back(out);
        inDegree[out]++;
    }
    //现将入度为0的点入对
    for(int i = 1;i <= n;i++)
    {
        if (0 == inDegree[i])
        {
            stk.push(i);
        }
    }
}
//拓扑排序
void TopSort()
{   
    vector<int> res;
    int v;
    while (!stk.empty())
    {
        //取出入度为0的点
        v = stk.front();
        stk.pop();
        //遍历该点的所有边，判断是否有入度为0的点
        for(auto it = adj[v].begin();it != adj[v].end();it++)
        {
            inDegree[*it]--;
            if (inDegree[*it] == 0)
            {
                stk.push(*it);
            }
            
        }
        res.push_back(v);
        cout << v << " ";
        //如果所有点都已加入到res中,就结束循环
        if (res.size() == (inDegree.size() - 1))
        {
            break;
        }
    }
    if (res.size() != (inDegree.size()-1))
    {
        cout << "Error" << endl;
    }
    for(int i = 0;i < res.size();i++)
    {
        cout << res[i];
        if (i != res.size() - 1)
        {
            cout << " ";
        }
    }
}
int main() {
    CreateGraph();
    TopSort();
    return 0;
}