机器学习整理（逻辑回归）

二分类问题

问题定义：给定一些特征，给其分类之一。
假设函数 \(h(x)\) 定义：

\[h(x) = g(\theta^Tx) \]

\[g(z) = \dfrac{1}{1 +e^{-z}} \]

决策边界：

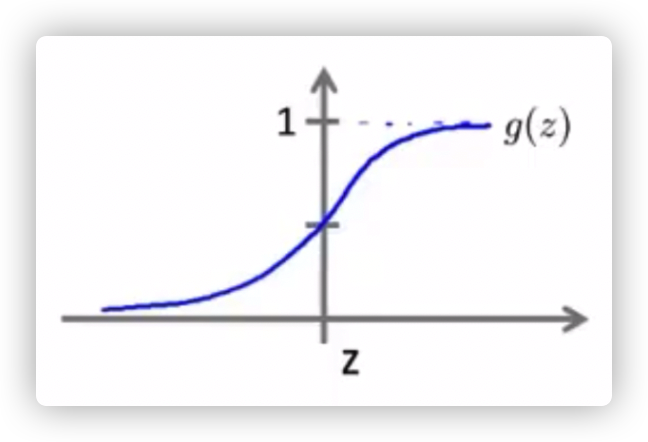
当 \(h(x) >= 0.5\) 的时候，y 更有可能预测为 1。

当 \(h(x) < 0.5\) 的时候，y 更有可能预测为 0。

当 z 的值为 0，也就是 \(\theta^Tx\) = 0 时就是区分两种分类的决策边界。
决策边界可能是直线，也有可能是曲线、圆。

代价函数

\(g(x)\) 是一个“非凸函数”，如果将点距离公式带入到逻辑回归中，就会存在很多局部最优解。
新的代价函数定义：

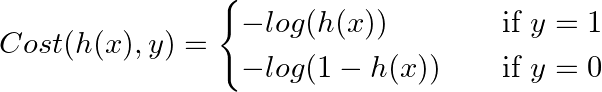
定义的代价函数图像和原因如下：

如果预测是/接近 0，但是实际的y是 1，这样代价函数的值就会非常大，以此来惩罚（修正）代价函数，而我们需要将代价函数最小化才能计算出 \(h(x)\) 的参数 θ。

因为总是存在 $y = 0 $ 或 \(y = 1\) ，所以可以将代价函数合并：

\[J(\theta) = -\frac{1}{m} [\sum_{i=1}^{m}y_ilog(h(x_i)) + (1-y_i)log(1-h(x_i)) ] \]

梯度下降的算法和之前一致，只不过偏导数相对复杂一些。

多分类问题

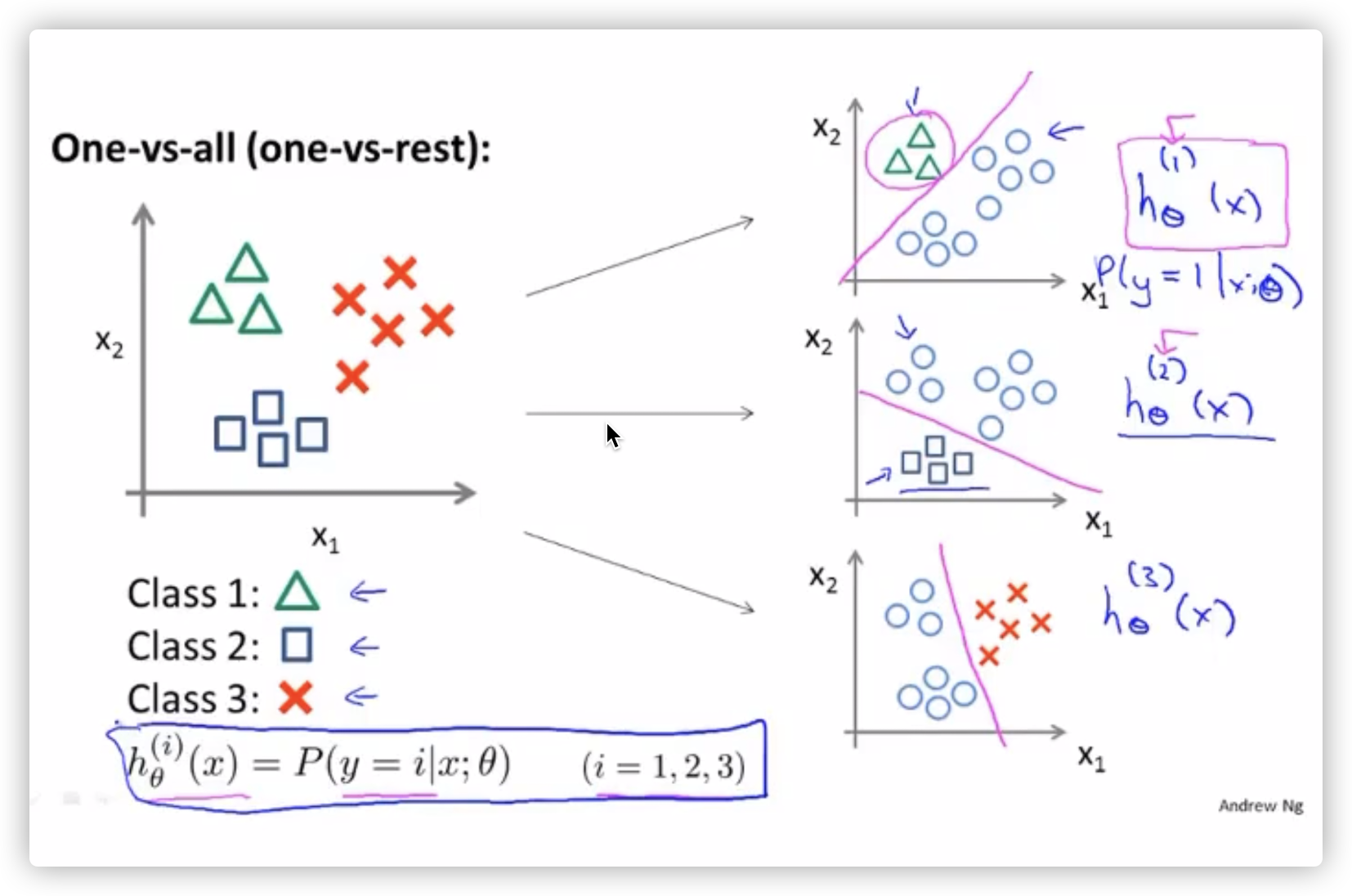
将多个类别的分类，转化成一对一的分类（分类器），每一个分类器相当于在计算属于自己那个分类的逻辑回归。

进行预测时：选择 \(max(h_i(x))\) 的分类器，也就是概率最高的一个，如图（右侧）。