图解NavMesh寻路中的漏斗算法
NavMesh是广泛使用的一种寻路技术，将地图中可走的部分生成连续的多边形/三角形网格，寻路在网格中进行，主要包含两步：1、根据网格的邻接信息构造图，使用A*之类的寻路算法计算出从起点到重点需要走过的多边形/三角形集合；2、使用漏斗算法/拉绳子算法，将多边形列表转换为一条最优的路店。本文主要讲一下对于三角形列表的漏斗算法原理。
诸位读者如果搜索过网络，会发现有一年GDC有人讲了这个算法，也有几篇博客翻译了这个GDC的演讲slides，但多半都是仅仅翻译一遍slides的水平，没有真的把算法说明白，导致笔者在实现这个算法的时候遇到了很大的困难，好在最后还是弄懂了。
如果你看到这行文字，说明这篇文章被无耻的盗用了（或者你正在选中文字），请前往 cnblogs.com/pointer-smq 支持原作者，谢谢
阅读本文需要一定的前置知识，您需要知道NavMesh及其对应的三角形网格，以及单位在NavMesh中寻路的三角形列表中间结果。
算法结果
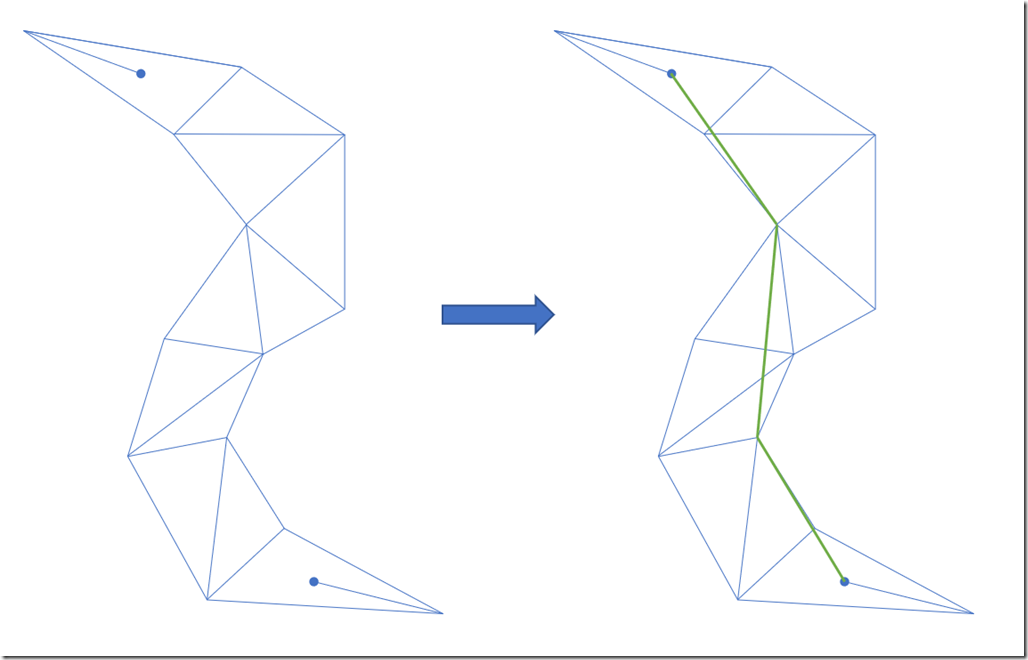
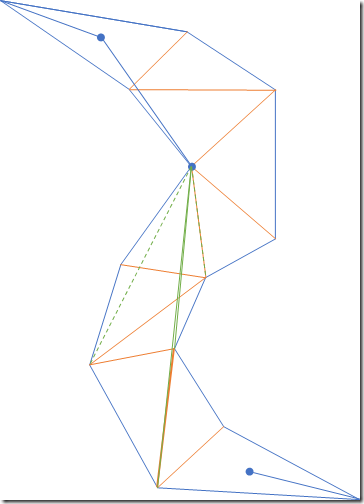
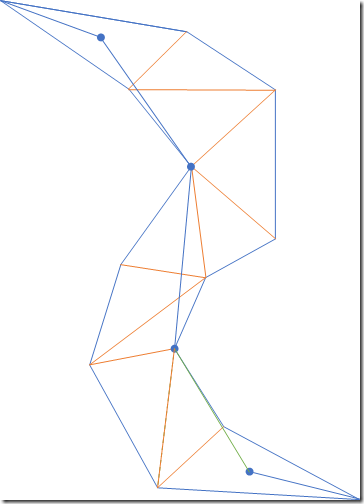
如图所示，假定左边的三角形列表是从寻路算法生成的从起点到终点需要经过的三角形，两个蓝色圆点分别是起点和重点；右边绿色的粗线就是算法的结果，是从起点到终点需要经过的最短路径。
算法过程
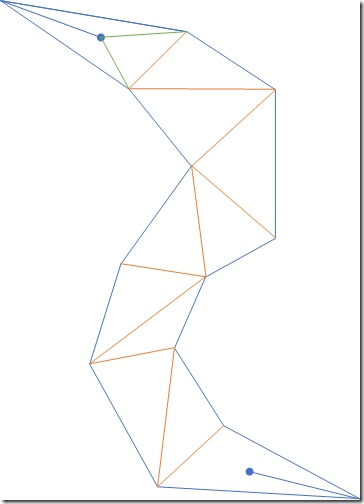
- 首先计算出三角形列表中的邻接边列表，所谓邻接边就是两个三角形公用的边，然后从起点开始，构造到第一条邻接边的漏斗，算法正式开始。
黄色的边均为邻接边，两条绿色的边为初始的漏斗，姑且约定两条“漏斗边”的“起点”为蓝色圆点，方便后文的描述
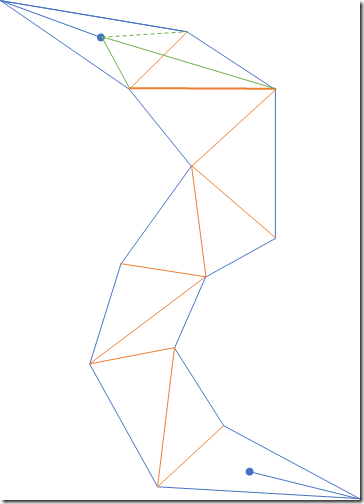
- 将两条漏斗边的终点移动到下一条邻接边，对于途中的情况，左边的边没有动（但逻辑上算移动了），右边的边向内收紧了。
分别考虑两条边的角度变化，当漏斗变窄（或不变化）时，本次移动是有效的，否则需要对那条边回退操作，对于图中情况，移动是有效的
可见图中的漏斗变窄了
- 继续将漏斗边的终点移动到下一条邻接边，漏斗继续收紧，移动有效，之后的两步操作都和上图情况相同
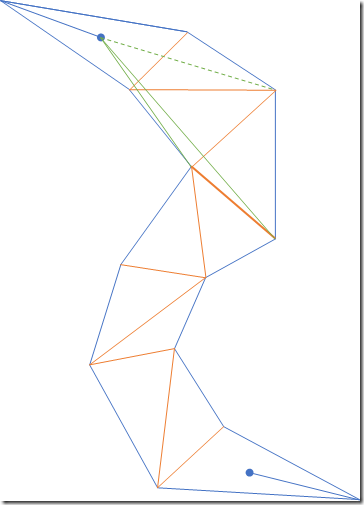
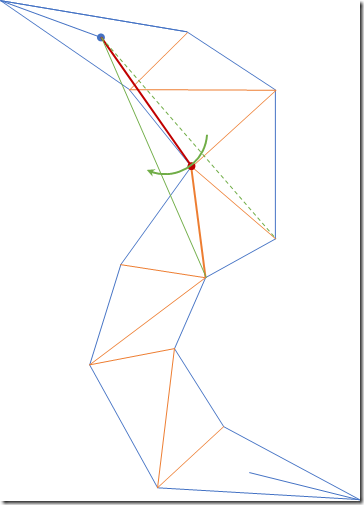
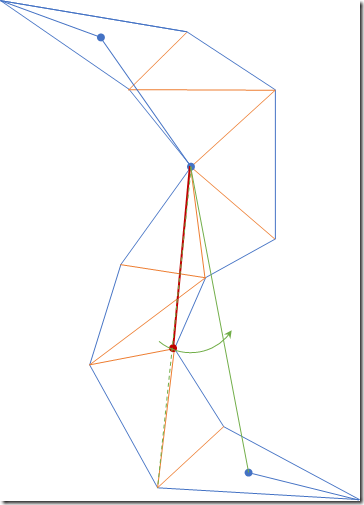
- 下一步操作出现了第一种特殊情况，漏斗边终点移动到下一条邻接边时，漏斗口的角度变为了负数（原来右边漏斗边转到了左边去），这种情况下，被盖过去的那条边的终点就成为了结果中的第一个点。
同时，将漏斗起点移动到该点，以当前漏斗起点所在三角形的出邻接边构造漏斗，继续算法
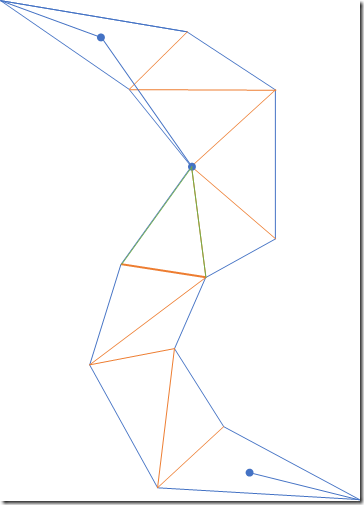
- 使用之前描述的规则继续收紧漏斗口
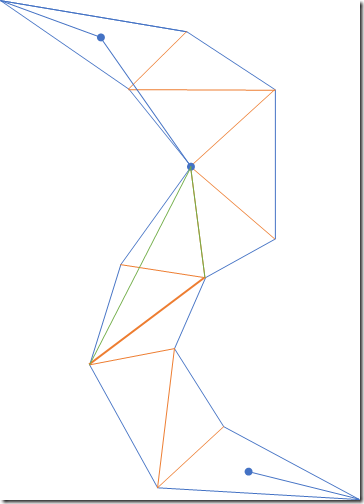
- 继续移动漏斗，这一次会发现左边的漏斗边没有移动，而右边的漏斗边会使漏斗口变大，右边的移动是无效的。这次移动只有左边发生了移动（虽然起点和终点一样）
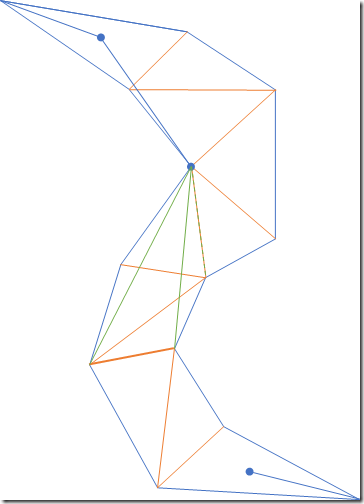
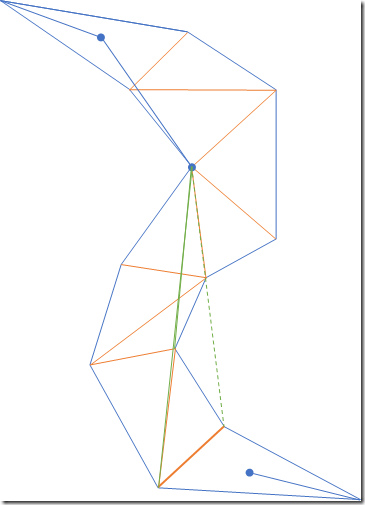
- 下面是算法的结束情况，算法已经移动到了最后一条邻接边，但是从现在的漏斗底直接连一条线到终点肯定是不可行的。随后我们以终点一个点，当作一条两条端点相同的边。用它继续前进漏斗口。
右边的漏斗边如果移动，会使漏斗口变大，因此不移动，左边的漏斗边移动，会盖过右边的漏斗边，因此右边的漏斗边终点成为了结果中的另一个点。
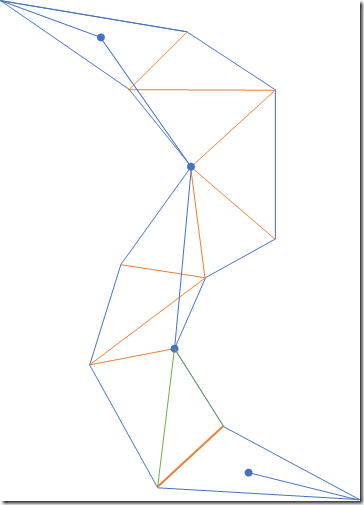
- 同样，以该点所在三角形的出邻接边重新构造漏斗，继续算法，很快就会发现漏斗口到终点，收到了最小，算法结束。
