数字逻辑电路
前言
啊啊啊啊,不知道写啥
正文
1.1计数体制
掌握进制之间的转换即可。
整数的进制转换
十进制整数 \(n\) 转换到 \(k\) 进制数 \(m\)。
\(n = m = k^ba_b + k^{b - 1}a_{b - 1} + \dots + k^0a_0\)
\(\lfloor\dfrac{n}{k}\rfloor = k^{b - 1}a_b + k^{b - 2}a_{b - 1} + \dots + k^0a_1\)
\(n - k \times \lfloor\dfrac{n}{k}\rfloor = a_0\)
用此方法可以依次取出最低位。
示意
将十进制数 \(25\) 转换为 \(2\) 进制。
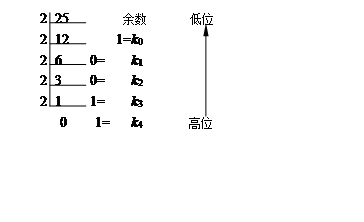
\(a\) 进制整数转换到 \(b\) 进制
一种方法是先转换为十进制再转换为 \(b\) 进制。
另一种方法是在 \(a\) 进制下使用 \(10\) 进制转换的方法。
小数的进制转换
十进制小数 \(n\) 转换到 \(k\) 进制小数 \(m\)。
\(n = m = k^{-1}a_1 + k^{-2}a_{2} + \dots + k^{-b}a_b\)
\(n \times k = k^{0}a_1 + k^{-1}a_{2} + \dots + k^{1-b}a_b\)
每次取整数位可以依次取出最高位。
示意
将十进制小数 \(0.6875\) 转换到 \(2\) 进制小数。

\(a\) 进制小数转换到 \(b\) 进制
一种方法是先转换为十进制再转换为 \(b\) 进制。
另一种方法是在 \(a\) 进制下使用 \(10\) 进制转换的方法。
1.2带符号数的代码表示
掌握原码反码补码
原码在二进制前加了一位符号位,值为负符号位为 \(1\),值为正符号位为 \(0\),正数原码反码补码相同。
负数反码将符号位以外的位取反,负数补码在反码基础上的最低位加 \(1\)。
原码中有两个 \(0\) 分别为 \(+0 = 0000 0000\),\(-0 = 1000 0000\)。 原码从 \(0000 0000 \sim 1111 1111\) 表示的值为 \(+0 \sim 2 ^ 7 - 1,-0 \sim - 2 ^ 7 + 1\)
反码中也有两个 \(0\) 分别为 \(+0 = 0000 0000\),\(-0 = 1111 1111\)。反码从 \(0000 0000 \sim 1111 1111\) 表示的值为 \(+0 \sim 2 ^ 7 - 1, -2^7 + 1 \sim -0\)
补码中只有一个 \(0\),\(0000 0000\)。补码从 \(0000 0000 \sim 1111 1111\) 表示的值为 \(+0 \sim 2 ^ 7 - 1, -2^7 \sim -1\)
几个记住会方便计算的什么东西
若 \([x]_{\text{补}} = x_0x_1\dots x_{n-1}\)
则有
\(x = (-x_0)2^{n-1}+\sum\limits_{i = 1}^{n - 1}x_i\times 2^{n - 1 - i}\)
\([\dfrac{x}{2}]_{\text{补}} = x_0x_0x_1\dots x_{n-2}.x_{n-1}\)
\([-x]_{\text{补}} = \overline{x_0}\overline{x_1}\dots \overline{x_{n-1}} + 1\)
1.3十进制数的二进制编码(BCD码)
8421BCD码
用四位二进制表示一位十进制。
四位二进制 \(abcd\) 表示的是十进制 \(8a+4b+2c+d\)。即从左到右的权重为 \(8,4,2,1\)。
\(1010 \sim 1111\) 这几个编码是用不上的。
余3码
和 \(8421BCD\) 码相同,用四位二进制表示一位十进制,但在 \(8421BCD\) 码的基础上加了\(3\)。
\(0011\) 在 \(8421BCD\) 码中表示 \(3\),在余 \(3\) 码中表示 \(0\)。
2421BCD码
用四位二进制表示一位十进制。
四位二进制 \(abcd\) 表示的是十进制 \(2a+4b+2c+d\)。即从左到右的权重为 \(2,4,2,1\)。
\(0000 \sim 1111\) 共 \(16\) 个编码全部使用了。
需要注意的是对于一个十进制数可能有多种 \(2421BCD\) 码编码方式
1.4 可靠性编码
典型格雷码
格雷码(没错,就是那个 \(noip\) 还是 \(csp\) 中不小心会溢出的格雷码)
格雷码需要满足相邻的两个数只有一位不同,如此松的要求就使得格雷码有多种形式。
典型格雷码与二进制之间有简单的转换关系,是唯一的。
编码方式
设二进制码为 \(B=B_{n}B_{n-1}\dots B_1B_0\),其对应的格雷码为 \(G=G_{n}G_{n-1}\dots G_1G_0\),则有
格雷码为什么是可靠性编码?我不知道。
奇偶校验码
奇偶校验码由信息位和校验位两部分组成。信息位是要传送的信息本身,位数不限;校验位是附加的冗余位,仅使用一位。
编码方式
- 校验位使得奇偶校验码中 \(1\) 的个数为奇数,称为奇校验;
- 校验位使得奇偶校验码中 \(1\) 的个数为偶数,称为偶校验。
设信息位为 \(C_1 C_2 \dots C_n\),有
对于奇校验,校验位 \(P = C_1 \oplus C_2 \oplus \dots \oplus C_n \oplus 1\)
对于偶校验,校验位 \(P = C_1 \oplus C_2 \oplus \dots \oplus C_n\)
由以上编码方式可以发现奇偶校验码能够发现有奇数位出错的情况,不能定位错误也不能纠正错误。
海明码
海明码的基础是奇偶校验。
编码方式
海明码也是由信息位和校验位构成,校验位的长度 \(m\) 由信息位的长度 \(n\) 决定 \((m = \lceil log_2^n \rceil)\)。校验位全部位于海明码的 \(2^i(i=0,1,2,\dots,m)\) 位上,信息码则按顺序排列在剩余位置上。
若信息位为 \(a_1a_2\dots a_{11}\),校验位为 \(b_1b_2b_3b_4\),则海明码为 \(b_1b_2a_1b_3a_2a_3a_4b_4a_5a_6a_7a_8a_9a_{10}a_{11}\)。
设海明码从左到右的编号为 \(1,2,\dots n + m\)。对于编号 \(j\) 如果这一位是信息位且 \((j >> (i - 1)) \& 1 = 1(i=0,1,2,\dots,m)\) 则 \(b_i\) 就要异或上这一位(偶校验)。
用 \(b_1b_2a_1b_3a_2a_3a_4b_4a_5a_6a_7a_8a_9a_{10}a_{11}\) 来举例子。
\(b_1 = a_1\oplus a_2 \oplus a_4 \oplus a_5 \oplus a_7\oplus a_9\oplus a_{11}\)
\(b_2 = a_1\oplus a_3 \oplus a_4 \oplus a_6 \oplus a_7\oplus a_{10}\oplus a_{11}
\)
\(b_2 = a_2\oplus a_3 \oplus a_4 \oplus a_8 \oplus a_9\oplus a_{10}\oplus a_{11}
\)
\(b_2 = a_5\oplus a_6 \oplus a_7 \oplus a_8 \oplus a_9\oplus a_{10}\oplus a_{11}
\)
如此一来就完成了偶校验的编码,奇校验要再异或 \(1\)。
校验方法
设 \(S_i\) 等于 \(b_i\) 再异或上求 \(b_i\) 用到的信息位。
如 \(S_1 = b_1 \oplus a_1\oplus a_2 \oplus a_4 \oplus a_5 \oplus a_7\oplus a_9\oplus a_{11}\)。
出错的即是海明码中的第 \(S_mS_{m-1}\dots S_1\) 位,多位出错不会,课本上没讲。奇校验也不会课本上没讲,有时间再来研究。
结语
啊啊啊啊啊,考试前还来得及吗。
待办
- 给海明码添加表格
- 海明码奇校验,多位出错
- 完整知识
- 一些题目


