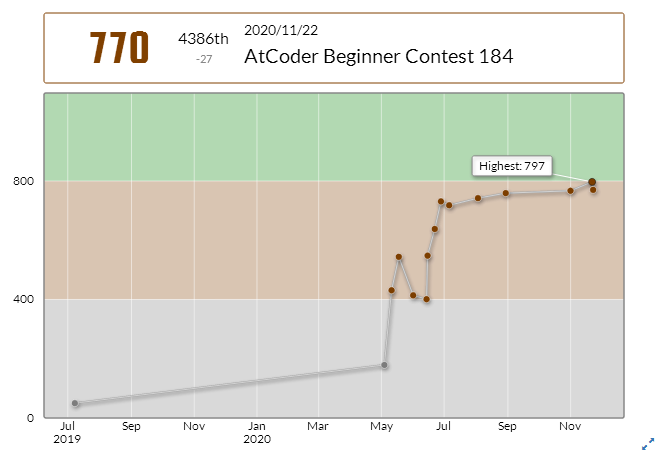
「赛后总结」AtCoder Beginner Contest 184
题意 & 题解
A.Determinant
题意:
给你 \(a,b,c,d\),计算 \(ad-ba\)。
题解:
签到题。
#include <cstdio>
#include <iostream>
int main() {
int a, b, c, d;
scanf("%d %d %d %d", &a, &b, &c, &d);
std::cout << a * d - b * c << '\n';
return 0;
}
B.Quizzes
题意:
已有分数 \(X\),读到 x 并且 \(X>0\) 则 \(X-1\),读到 o 则 \(X + 1\)。
题解:
签到题。
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
int n, x;
std::string s;
int main() {
std::cin >> n >> x >> s;
for (int i = 0; i < n; ++i) {
if (s[i] == 'o') ++x;
if (s[i] == 'x' && x) --x;
}
std::cout << x << '\n';
return 0;
}
C.Super Ryuma
题意:
给一个起点一个终点,可以往当前点所在在对角线或者曼哈顿距离为 \(3\) 以内的整点上跳,问最少几步到达终点。
题解:
最多跳三次。
如果起点终点重合,共零次。如果终点在起点能跳到的点上,共一次。两个点的对角线一定有个交点,如果是横坐标整数可以先跳到交点再往终点跳,还有其他跳的方式,不细说了,共两次。如果不是整数可以先跳到终点的对角线附近,再跳到对角线上,再跳一次,共三次。
#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
long long r1, c1, r2, c2;
int main() {
std::cin >> r1 >> c1 >> r2 >> c2;
if (r1 == r2 && c1 == c2) return puts("0"), 0;
if (r1 + c1 == r2 + c2 || r1 - c1 == r2 - c2 || abs(r1 - r2) + abs(c1 - c2) <= 3) return puts("1"), 0;
bool flag = false;
if ((r2 + c2 + r1 - c1) % 2 == 0 || (r1 + c1 + r2 - c2) % 2 == 0) return puts("2"), 0;
for (int i = r1 - 3; i <= r1 + 3; ++i) {
for (int j = c1 - 3; j <= c1 + 3; ++j) {
if (abs(r1 - i) + abs(c1 - j) > 3) continue;
if (i + j == r2 + c2 || i - j == r2 - c2 || abs(i - r2) + abs(j - c2) <= 3) flag = true;
}
}
for (int i = r2 - 3; i <= r2 + 3; ++i) {
for (int j = c2 - 3; j <= c2 + 3; ++j) {
if (abs(r2 - i) + abs(c2 - j) > 3) continue;
if (i + j == r1 + c1 || i - j == r1 - c1 || abs(i - r1) + abs(j - c1) <= 3) flag = true;
}
}
if (flag) return puts("2"), 0;
return puts("3"), 0;
}
D.increment of coins
题意:
初始时有 \(a\) 个金币,\(b\) 个银币,\(c\) 个铜币,每次可以随机取出一个 \(x\) 并放入两个相同的 \(x\)。当出现 \(100\) 个相同的币时停止,问操作次数的期望。
题解:
\(f_{i,j,k}\) 表示 \(i\) 个金币,\(j\) 个银币,\(k\) 个铜币到结束的操作次数的期望。
下一步可以到 \(f_{i+1,j,k}\)、\(f_{i,j + 1,k}\)、\(f_{i,j,k + 1}\) 三种状态。
\(f_{i,j,k} = (f_{i+1,j,k}+1)\times\frac{i}{i+j+kj} + (f_{i,j+1,k}+1)\times\frac{j}{i+j+kj}+(f_{i,j,k+1}+1)\times\frac{k}{i+j+kj}\)
个人感觉记忆化搜索比较好写。
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#define M 101
int a, b, c;
double f[M][M][M];
double dfs(int x, int y, int z) {
if (x >= 100 || y >= 100 || z >= 100) return 0;
if (f[x][y][z] != -1) return f[x][y][z];
f[x][y][z] = (dfs(x + 1, y, z) + 1) * ((x * 1.0) / (1.0 * (x + y + z)));
f[x][y][z] += (dfs(x, y + 1, z) + 1) * ((y * 1.0) / (1.0 * (x + y + z)));
f[x][y][z] += (dfs(x, y, z + 1) + 1) * ((z * 1.0) / (1.0 * (x + y + z)));
return f[x][y][z];
}
int main() {
for (int i = 0; i <= 100; ++i) {
for (int j = 0; j <= 100; ++j) {
for (int k = 0; k <= 100; ++k) {
f[i][j][k] = -1;
}
}
}
std::cin >> a >> b >> c;
printf("%.9lf\n", dfs(a, b, c));
return 0;
}
E.Third Avenue
题意:
一个地图,可以向上下左右走,相同的小写字母可以互相传送,每一个操作都要一秒时间,问从起点到终点要耗费的最短时间。
题解:
字母只会在第一次遇到时进行传送,所以直接宽搜。
F.Programming Contest
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#define M 2001
typedef std::pair<int, int> pii;
std::queue<pii> q;
std::vector<pii> V[27];
std::string map[M];
int n, m, a, b, d[M][M];
bool vis[M][M], used[M], f;
int dx[5] = {0, 1, -1, 0, 0};
int dy[5] = {0, 0, 0, 1, -1};
void bfs(int sx, int sy) {
q.push(std::make_pair(sx, sy));
d[sx][sy] = 0, vis[sx][sy] = true;
while (!q.empty()) {
int x = q.front().first, y = q.front().second; q.pop();
if (map[x][y] == 'G') { f = 1, printf("%d\n", d[x][y]); return; }
for (int i = 1; i <= 4; ++i) {
int x_ = x + dx[i], y_ = y + dy[i];
if (x_ <= 0 || x_ > n || y_ < 0 || y_ >= m) continue;
if (map[x][y] == '#' || vis[x_][y_]) continue;
vis[x_][y_] = true, d[x_][y_] = d[x][y] + 1;
q.push(std::make_pair(x_, y_));
}
if (map[x][y] < 'a' || map[x][y] > 'z' || used[map[x][y] - 'a']) continue;
used[map[x][y] - 'a'] = true;
for (int i = 0; i < V[map[x][y] - 'a'].size(); ++i) {
int x_ = V[map[x][y] - 'a'][i].first, y_ = V[map[x][y] - 'a'][i].second;
if (vis[x_][y_]) continue;
vis[x_][y_] = true, d[x_][y_] = d[x][y] + 1;
q.push(std::make_pair(x_, y_));
}
}
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i) std::cin >> map[i];
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < m; ++j) {
if (map[i][j] == 'S') a = i, b = j;
if (map[i][j] >= 'a' && map[i][j] <= 'z') {
V[map[i][j] - 'a'].push_back(std::make_pair(i, j));
}
}
}
bfs(a, b);
if (!f) puts("-1");
return 0;
}
题意:
给定 \(n\) 个数以及一个 \(t\),你要找到若干数的和使它最大并且不超过 \(t\)。
题解:
\(n \le 40\),用折半搜索搜出前 \(20\) 个数和后 \(20\) 个数的选法之后用二分进行配对。
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#define M 21
int min(int a, int b) { return a < b ? a : b; }
int max(int a, int b) { return a > b ? a : b; }
int n, m, t, c1, c2, a[M], b[M];
int ans, ans1[1 << M], ans2[1 << M];
void dfs1(int step, int now) {
if (now > t) return;
if (step > n) { ans1[++c1] = now; return; }
for (int i = 0; i <= 1; ++i) {
if (i == 1) dfs1(step + 1, now + a[step]);
if (i == 0) dfs1(step + 1, now);
}
}
void dfs2(int step, int now) {
if (now > t) return;
if (step > m) { ans2[++c2] = now; return; }
for (int i = 0; i <= 1; ++i) {
if (i == 1) dfs2(step + 1, now + b[step]);
if (i == 0) dfs2(step + 1, now);
}
}
int main() {
scanf("%d %d", &n, &t);
m = n - 20, n = min(n, 20);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= m; ++i) scanf("%d", &b[i]);
dfs1(1, 0);
if (m > 0) dfs2(1, 0);
std::sort(ans1, ans1 + c1 + 1);
std::sort(ans2, ans2 + c2 + 1);
for (int i = 0; i <= c1; ++i) {
int temp = t - ans1[i];
int pos = std::lower_bound(ans2, ans2 + c2 + 1, temp) - ans2;
if (pos == c2 + 1 || ans2[pos] > temp) --pos;
ans = max(ans, ans1[i] + ans2[pos]);
}
std::cout << ans << '\n';
return 0;
}
rating & 总结
-
只做出了前两题,很不应该。
-
F 做过类似的题但是考场上就是没想起来/kk