「学习笔记」哈密尔顿通路&哈密尔顿回路
感想
在有限的 OIer 生涯中应该再也不会去研究这种东西了。在 OI 界太冷门了。
艹,清北学堂国庆的Day4T4好像和哈密尔顿通路有关,我是毒奶?

概念
哈密尔顿通路:图 \(G\) 中一条从 \(S\) 到 \(T\) 的路径不重不漏地经过了每个点,那么这条路径称为哈密尔顿通路。
哈密尔顿回路:图 \(G\) 中一条从 \(S\) 到 \(S\) 的路径不重不漏地经过了除 \(S\) 外每个点并且 \(S\) 只经过过两次,那么这条路径称为哈密尔顿回路。
哈密尔顿图:若图 \(G\) 中存在哈密尔顿回路则称 \(G\) 为哈密尔顿图。
\(N\) 阶竞赛图:含有 \(N\) 个顶点的有向图,且每对顶点之间都有一条边(不限定方向)。
无向简单图:不含重边和自环的无向图。
求解方法
求解哈密尔顿通路
充分条件:
设 G 是有 \(n\) 个点的无向简单图(\(n \geq 2\)),若 \(G\) 中任意不相邻的两点 \(u,v\) 都满足 \(d(u) + d(v) \geq n - 1\),则 \(G\) 有哈密尔顿通路。
是下面涉及到的Ore定理的推论。
可以转化成求哈密尔顿回路:
枚举哈密尔顿通路的起点 \(S\) 和终点 \(T\),在 \(S\) 和 \(T\) 之间加一条边,判断是否存在哈密尔顿通路。
\(N(N\geq2)\)阶竞赛图中一定存在哈密尔顿通路
证明:
很显然 \(N = 2\) 时成立(自己画图看看就行)。
\(N = k\) 时是成立的,去证明 \(N = k + 1\) 时是成立的。
设 \(N = k\) 时存在的哈密尔顿通路为 \(v_1,v_2,\dots,v_k\)。(下标只是代表在走的时候经过的顺序)
从 \(i = k \sim 1\) 去看 \(v_i\) 和 \(v_{k+1}\) 的联通情况。
若存在 \(v_i\) 指向 \(v_{k+1}\) 的边,那么存在 \(v_1,\dots,v_i,v_{k+1},v_{i+1},\dots,v_k\) 这样一条通路。
否则存在 \(v_{k+1},v_1,v_2,\dots,v_k\) 这样一条通路。
证毕。
在竞赛图中找哈密尔顿通路的代码(就是模拟上述过程):
//感觉时间复杂度是 O(n ^ 3)
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#define M 6180
int n, m, now, ans[M];
bool p[M][M];
void ins(int pos, int x) {
int temp;
++now;
for (int i = pos; i <= now; ++i) {
temp = ans[i], ans[i] = x, x = temp;
}
}
void hamilton() {
now = 2, ans[1] = 1;
for (int i = 2; i <= n; ++i) {
bool okay = false;
for (int j = now - 1; j >= 1; --j) {
if (p[ans[j]][i]) {
okay = true;
ins(j + 1, i);
break;
}
}
if (!okay) ins(1, i);
}
}
int main() {
scanf("%d", &n);
m = n * (n - 1) / 2;
for (int i = 1, u, v; i <= m; ++i) {
scanf("%d %d", &u, &v);
if (u < v) p[u][v] = 1;
}
hamilton();
for (int i = 1; i <= n; ++i) printf("%d\n",ans[i]);
return 0;
}
求解哈密尔顿回路
是个NP-完全问题,好像没什么好的求解方法,都是根据一些充分条件/必要条件去构造的鸭子。
必要条件:
\(G\{V,E\}\) 是哈密尔顿图。
那么对于 \(V\) 的任意非空子集 \(V'\) 都有:\(P(G-V') \leq |V'|)\)(其中 \(P(G)\) 表示图 \(G\) 的连通分量个数,\(|V'|\) 表示 \(V'\) 中元素个数,\(G-V'\) 表示从 \(G\) 中删掉 \(V'\) 中的元素后得到的图)。
证明:
设 \(G\) 中的哈密尔顿回路为 \(C\),那么 \(P(G-V')\leq P(C-V')\)。因为往 \(C-V'\) 这个图中加边连通分量的数量是不会改变的。
只需要证明 \(P(C-V') \leq |V'|\) 即可。
\(C\) 一定是个环,开始删点,删掉的第一个点使得 \(C\) 不再是一个环,之后每次删点最多增加一个连通分量,也就是最多有 \(|V'|\) 个连通分量。
证毕。
这只是个必要条件,下图满足这个条件但不是哈密尔顿图。
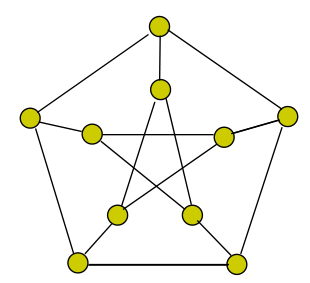
必要条件的推论:
\(G\{V,E\}\) 中有哈密尔顿通路。那么对于 \(V\) 的任意非空子集 \(V'\) 都有:\(P(G-V') \leq |V'| + 1)\)。
证明类似于上面那个证明,不再重复证了。
几个示例:
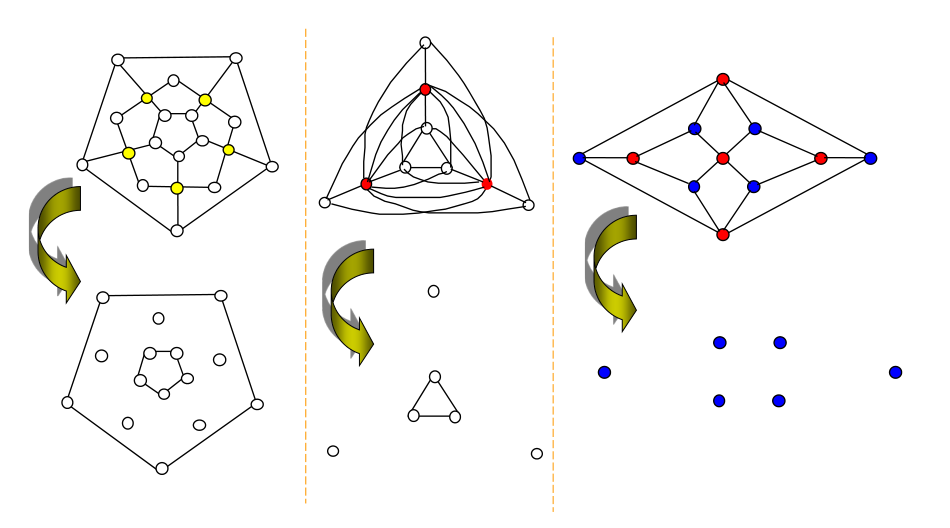
以下是充分条件
Dirac 定理:
设 G 是有 \(n\) 个点的无向简单图(\(n \geq 3\)),若 \(G\) 中每个节点的度数至少为 \(\left\lceil\frac{n}{2}\right\rceil\),则 \(G\) 为哈密尔顿图。
Ore 定理:
设 G 是有 \(n\) 个点的无向简单图(\(n \geq 3\)),若 \(G\) 中任意不相邻的两点 \(u,v\) 都满足 \(d(u) + d(v) \geq n\),则 \(G\) 为哈密尔顿图。
证明鸽了。
在满足 Dirac 定理的情况下找哈密尔顿回路(不保证正确)。
//复杂度好像是 O(n ^ 2)
#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#define M 1001
int n, m, now, d[M], ans[M];
bool map[M][M], used[M];
void reverse(int l, int r) {
int temp;
while (l < r) {
temp = ans[l];
ans[l] = ans[r];
ans[r] = temp;
++l, --r;
}
}
void hamilton() {
int s, t;
s = ans[1] = 1, now = 2, used[1] = true;
for (int i = 2; i <= n; ++i) {
if (map[1][i]) {
t = ans[2] = i;
used[i] = true;
break;
}
}
while (true) {
while (true) {
bool okay = false;
for (int i = 1; i <= n; ++i) {
if (used[i]) continue;
if (map[t][i]) {
ans[++now] = i;
okay = true;
used[i] = true;
t = i; break;
}
}
if (!okay) break;
}
reverse(1, now);
s = ans[1], t = ans[now];
while (true) {
bool okay = false;
for (int i = 1; i <= n; ++i) {
if (used[i]) continue;
if (map[t][i]) {
ans[++now] = i;
okay = true;
used[i] = true;
t = i; break;
}
}
if (!okay) break;
}
if (!map[s][t]) {
int flag = -1;
for (int i = 2; i <= now - 2; ++i) {
if (map[t][ans[i]] && map[s][ans[i + 1]]) {
flag = i; break;
}
}
t = ans[flag + 1];
reverse(flag + 1, now);
}
if (now == n) break;
int flag1 = -1, flag2 = -1;
for (int i = 1; i <= n; ++i) {
flag1 = i;
if (used[i]) continue;
for (int j = 1; j <= now - 2; ++j) {
if (map[ans[j]][i]) {
flag2 = j;
break;
}
}
if (flag2 != -1) break;
}
s = ans[flag2 - 1], t = flag1;
reverse(1, flag2), reverse(flag2 + 1, now);
ans[++now] = flag1;
used[flag1] = true;
}
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1, u, v; i <= n; ++i) {
scanf("%d %d", &u, &v);
++d[u], ++d[v];
map[u][v] = map[v][u] = true;
}
for (int i = 1; i <= n; ++i) {
if (d[i] < ceil(1.0 * n / 2.0)) {
puts("This does not conform to Dirac's theorem");
return 0;
}
}
hamilton();
for (int i = 1; i <= n; ++i) printf("%d ", ans[i]);
return 0;
}
To Be Continued


