「题解」poj 3728 The merchant
题目
简化题意
给你一棵树,点有点权,到达一个点你可以花费该点的点权买入一个东西,然后在另一个点把这个东西卖出(卖出的时候手上必须有东西),只能买入卖出一次,问你从一个点 \(u\) 到一个点 \(v\) 的路径上能获得的最大收益。
思路
倍增。
除了正常倍增需要维护的东西还要维护下面这些:
\(maxx[i][j]\),表示在 \(i\) 到从 \(i\) 跳 \(2 ^ j\) 步到达的那个点之间的路径上的最大点权。
\(minn[i][j]\),表示在 \(i\) 到从 \(i\) 跳 \(2 ^ j\) 步到达的那个点之间的路径上的最小点权。
\(up[i][j]\),表示在 \(i\) 到从 \(i\) 跳 \(2 ^ j\) 步到达的那个点之间的路径上按 \(i \rightarrow i ^ j\) 的顺序能获得的最大收益。
\(down[i][j]\),表示在 \(i\) 到从 \(i\) 跳 \(2 ^ j\) 步到达的那个点之间的路径上按 \(i ^ j \rightarrow i\) 的顺序能获得的最大收益。
对于 \(u \rightarrow v\),进行分类讨论,如下图。
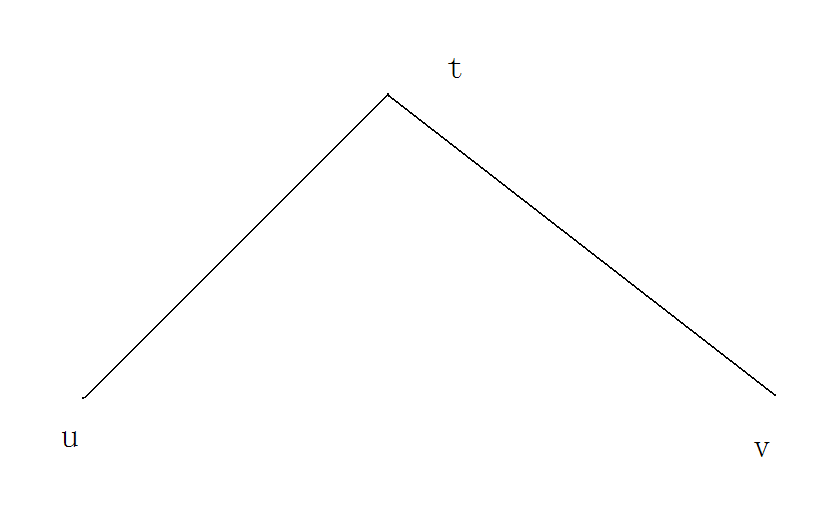
\(t\) 是 \(u\) 和 \(v\) 的最近公共祖先。
-
可能在 \(u \rightarrow t\) 的路径上获得最大收益,即在 \(u \rightarrow t\) 上买卖。
-
可能在 \(t \rightarrow v\) 的路径上获得最大收益,即在 \(t \rightarrow v\) 上买卖。
-
可能在 \(u \rightarrow t\) 上买,在 \(t \rightarrow v\) 上卖。
\(u \rightarrow t\) 和 \(t \rightarrow v\) 上获得的最大收益需要使用倍增来维护,类似求最近公共祖先时将两点跳到同一高度的操作。
在 \(u \rightarrow t\) 上买,在 \(t \rightarrow v\) 上卖的话只需要在算上面两种情况的时候同时求一下 \(u \rightarrow t\) 上的最小值和 \(t \rightarrow v\) 上的最大值即可。
Code
#include <cstdio>
#include <cstring>
#include <cstring>
#include <iostream>
#include <algorithm>
#define MAXN 50001
#define inf 2147483647
int max(int a, int b) { return a > b ? a : b; }
int min(int a, int b) { return a < b ? a : b; }
int n, m, pthn, a[MAXN], head[MAXN];
int lg[MAXN], fa[MAXN][21], dep[MAXN];
int maxx[MAXN][21], minn[MAXN][21], up[MAXN][21], down[MAXN][21];
struct Edge {
int next, to;
}pth[MAXN << 1];
void add(int from, int to) {
pth[++pthn].to = to, pth[pthn].next = head[from];
head[from] = pthn;
}
void dfs(int u, int father) {
maxx[u][0] = max(a[u], a[father]);
minn[u][0] = min(a[u], a[father]);
up[u][0] = max(0, a[father] - a[u]);
down[u][0] = max(0, a[u] - a[father]);
fa[u][0] = father, dep[u] = dep[father] + 1;
for (int i = head[u]; i; i = pth[i].next) {
int x = pth[i].to;
if (x != father) dfs(x, u);
}
}
int lca(int x, int y) {
if (dep[y] > dep[x]) std::swap(x, y);
while (dep[x] > dep[y]) {
x = fa[x][lg[dep[x] - dep[y]] - 1];
}
if (x == y) return x;
for (int k = lg[dep[x]] - 1; k >= 0; --k) {
if (fa[x][k] != fa[y][k]) {
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int getup(int s, int t, int &min_) {
int up_ = 0;
while (dep[s] > dep[t]) {
int step = lg[dep[s] - dep[t]] - 1;
up_ = max(up_, max(up[s][step], maxx[s][step] - min_));
min_ = min(min_, minn[s][step]);
s = fa[s][step];
}
return up_;
}
int getdown(int s, int t, int &max_) {
int down_ = 0;
while (dep[s] > dep[t]) {
int step = lg[dep[s] - dep[t]] - 1;
down_ = max(down_, max(down[s][step], max_ - minn[s][step]));
//std::cout << max_ << " " << s << " " << step << " " << maxx[s][step] << '\n';
max_ = max(max_, maxx[s][step]);
s = fa[s][step];
//std::cout << max_ << " " << s << " " << step << " " << maxx[s][step] << '\n';
}
return down_;
}
int main() {
//freopen("a.txt", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1, u, v; i < n; ++i) {
scanf("%d %d", &u, &v);
add(u, v), add(v, u);
}
for (int i = 1; i <= n; ++i) {
lg[i] = lg[i - 1] + ((1 << lg[i - 1]) == i);
}
dfs(1, 0);
for (int j = 1; (1 << j) <= n; ++j) {
for (int i = 1; i <= n; ++i) {
int temp = fa[i][j - 1];
fa[i][j] = fa[temp][j - 1];
maxx[i][j] = max(maxx[i][j - 1], maxx[temp][j - 1]);
minn[i][j] = min(minn[i][j - 1], minn[temp][j - 1]);
up[i][j] = max(max(up[i][j - 1], up[temp][j - 1]), maxx[temp][j - 1] - minn[i][j - 1]);
down[i][j] = max(max(down[temp][j - 1], down[i][j - 1]), maxx[i][j - 1] - minn[temp][j - 1]);
}
}
scanf("%d", &m);
for (int i = 1, u, v; i <= m; ++i) {
scanf("%d %d", &u, &v);
int l = lca(u, v), min_ = inf, max_ = 0;
int upmx = getup(u, l, min_);
int downmx = getdown(v, l, max_);
//std::cout << u << " " << v << " " << l << '\n';
//std::cout << upmx << " " << downmx << " " << min_ << " " << max_ << '\n';
int ans = max(max(upmx, downmx), max_ - min_);
printf("%d\n", ans);
}
return 0;
}

