「题解」洛谷 P1429 平面最近点对（加强版）

题目

P1429 平面最近点对（加强版）

思路

分治。

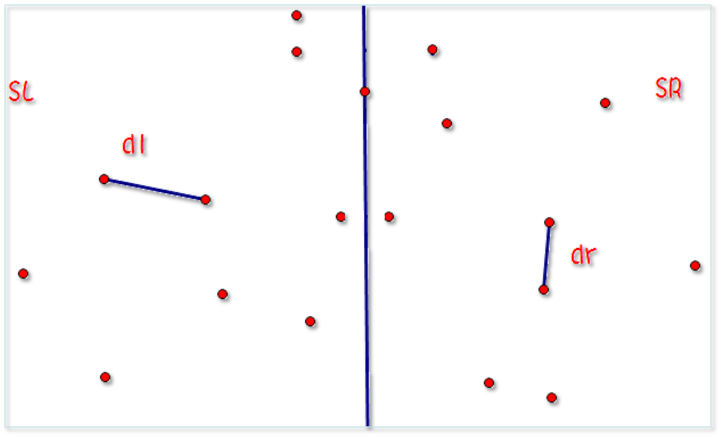
左边的最近距离为 \(dl\)，右边的最近距离为 \(dr\)。
如何得到整块的最近距离？
我们所需要做的就是计算两块之间距离小于 \(d = \min(dl, dr)\) 的点之间的距离然后取最小值。
先把两块中距离 \(mid\) 的水平距离小于 \(d\) 的点加入一个集合，然后按纵坐标排序暴力去计算距离。
可以证明在这个区域内距离小于 \(d\) 的点对有很少。

Code

#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#define MAXN 200001

double min(double a, double b) { return a < b ? a : b; }

int n, temp[MAXN];
struct point {
	double x, y;
	friend bool operator < (point p1, point p2) {
		if (p1.x == p2.x) return p1.y < p2.y;
		return p1.x < p2.x;
	}
}p[MAXN];

bool cmp(int a, int b) {
	return p[a].y < p[b].y;
}

double getd(int x, int y) {
	return sqrt((p[x].x - p[y].x) * (p[x].x - p[y].x) + (p[x].y - p[y].y) * (p[x].y - p[y].y));
}

double merge(int l, int r) {
	double d = 2147483647.0;
	if (l == r) return d;
	if (l == r - 1) return getd(l, r);
	int mid = (l + r) >> 1;
	double d1 = merge(l, mid);
	double d2 = merge(mid + 1, r);
	d = min(d1, d2);
	int cnt = 0;
	for (int i = l; i <+ r; ++i) {
		if (fabs(p[mid].x - p[i].x) < d) {
			temp[++cnt] = i;
		}
	}
	std::sort(temp + 1, temp + cnt + 1, cmp);
	for (int i = 1; i <= cnt; ++i) {
		for (int j = i + 1; j <= cnt && p[temp[j]].y - p[temp[i]].y < d; ++j) {
			d = min(d, getd(temp[i], temp[j]));
		}
	}
	return d;
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		scanf("%lf %lf", &p[i].x, &p[i].y);
	}
	std::sort(p + 1, p + n + 1);
	printf("%.4lf\n", merge(1, n));
	return 0;
}

思考

三维的怎么做？