各种排序(一)
- 本文中 \(n\) 代表着待排序序列的长度。
- 算法是否稳定:多个相同的元素,若排序后这几个元素的顺序改变了就不稳定,反之稳定。
冒泡排序
又叫气泡排序,起泡排序,泡沫排序
这应该是最简单的排序算法了吧。
在未排好序之前一直扫描序列,每次将最大数的放到序列的最后,所以最多 \(n-1\) 次扫描后序列就排好序了。
最差时间复杂度:\(O(n ^ 2)\)
最优时间复杂度:\(O(n)\)
平均时间复杂度:\(O(n ^ 2)\)
算法是否稳定:是
这么慢我要它有什么用。
for(int i=1;i<n;++i) {//n-1轮扫描
bool okay=true;
for(int j=1;j<=n-i;++j) {//[n-i+2,n]都已经排好序了。
if(a[j]>a[j+1]) {
swap(a[j],a[j+1]);
okay=false;
}
}
if(okay==true) break;
}
上几张动图,帮助理解。
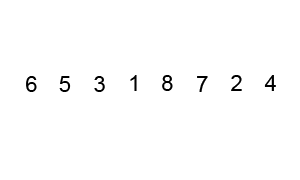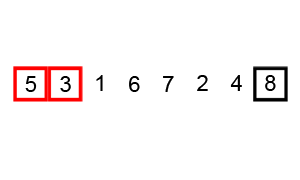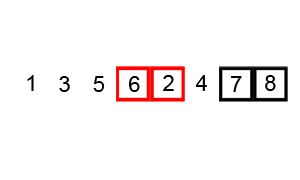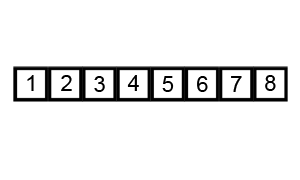
鸡尾酒排序
冒泡排序的一种优化。又叫做双向冒泡排序,鸡尾酒搅拌排序,搅拌排序,涟漪排序,来回排序或快乐小时排序。你【龙门粗口】名字真多。
有两种操作:
- 将序列中最大的数放到最后
- 将序列中最小的数放到最前
在未排好序之前将上面两种操作交替进行。
最差时间复杂度:\(O(n ^ 2)\)
最优时间复杂度:\(O(n)\)
平均时间复杂度:\(O(n ^ 2)\)
算法是否稳定:是
这么慢我要它有什么用。
好像没看出来哪里优
以 \(\{2,3,4,5,1\}\) 为例,冒泡排序需要 \(4\) 次(指的是扫描整个序列的次数):
\(\{2,3,4,5,1\} \rightarrow \{2,3,4,1,5\} \rightarrow \{2,3,1,4,5\} \rightarrow \{2,1,3,4,5\} \rightarrow \{1,2,3,4,5\}\)
而鸡尾酒排序只需要 \(2\) 次(指的是扫描整个序列的次数):
\(\{2,3,4,5,1\} \rightarrow \{2,3,4,1,5\} \rightarrow \{1,2,3,4,5\}\)
int left=1,right=n;//[left,right]需要排序。
while(left<right) {//最多进行到left=right就停止
bool okay=true;
for(int i=left;i<right;++i) {//将序列中最大的数放到最后
if(a[i]>a[i+1]) {
swap(a[i],a[i+1]);
okay=false;
}
}
if(okay==true) break;
--right;//[right+1,n]已经排好序了
for(int i=right;i>left;--i) {
if(a[i]<a[i-1]) {
swap(a[i],a[i-1]);
okay=false;
}
}
++left;//[1,left-1]已经排好序了
if(okay==true) break;
}
选择排序
在未排好序之前一直扫描序列,每次将最小数的放到序列的最前,所以最多 \(n-1\) 次扫描后序列就排好序了。
与冒泡排序的不同:冒泡排序每扫一次序列会进行多次交换,将不符合顺序的都交换。选择排序每扫一次序列只会进行一次交换,将最小的元素与最前的元素交换。
最差时间复杂度\(O(n ^ 2)\)
最优时间复杂度\(O(n ^ 2)\)
平均时间复杂度\(O(n ^ 2)\)
算法是否稳定:否
for(int i=1;i<n;++i) {//最多扫n-1次
bool okay=true;
int minn=0x7fffffff,flag;
for(int j=i;j<=n;++j) {
if(a[j]<minn) {
minn=a[j];flag=j;//找最小的并记录下位置。
okay=false;
}
}
if(okay==true) break;
std::swap(a[i],a[flag]);//将最小的元素与最前的元素交换
}
放张图理解一下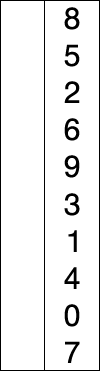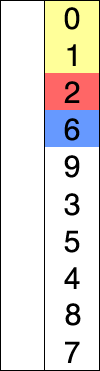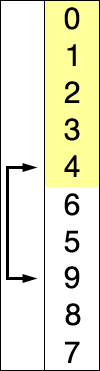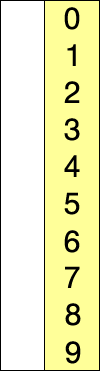
如{5,8,5,2,9},可知选择排序不稳定。
插入排序
流程就像是打牌的摸牌阶段。
操作将一个数插入到一个排好序的序列中时期仍然排好序即可。在序列基本有序或者序列长度小时效率很高。
最差时间复杂度:\(O(n ^ 2)\)
最优时间复杂度:\(O(n)\)
平均时间复杂度:\(O(n ^ 2)\)
算法是否稳定:是
for(int i=2;i<=n;++i) {//[1,i-1]已经排好了序
int temp=a[i],j=i-1;
while(j>0&&a[j]>temp) {//将第i张牌插入其中
a[j+1]=a[j];
j--;
}
a[j+1]=temp;
}
上张动图理解一下
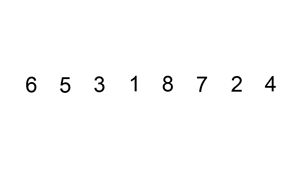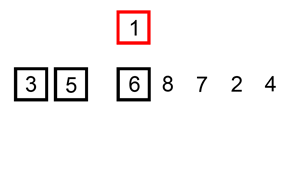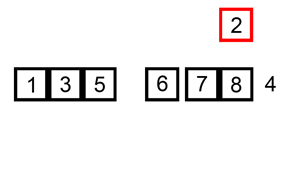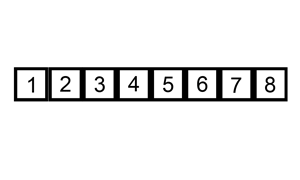
二分插入排序
在插入排序的基础上使用二分查找来确定当前数应该插入到哪里。
这是优化吗?我为什么感觉比插入排序还慢。
时间复杂度:\(O(n(log n + n))\)
算法是否稳定:是否
for(int i=2;i<=n;++i) {
int left=1,right=i-1,temp=a[i];
while(left<=right) {//二分查找当前数插入到哪里
int mid=(left+right)>>1;
if(a[mid]>temp) right=mid-1;
else left=mid+1;
}
for(int j=i-1;j>=left;--j) a[j+1]=a[j];
a[left]=temp;//插进去
}
对于if(a[mid]>temp) right=mid-1;
- 如果加了等号的话,不稳定排序
- 如果不加等号的话,是稳定排序
希尔排序
- 插入排序的特点:在序列基本有序或者序列长度小时效率很高。
运用了插入排序,现在我们有一个增量 \(x\) 一般为 \(\frac{n}{2}\) ,我们按照这个分量将整个序列分成 \(x\) 组,对每组进行插入排序(因为插入排序在需要排序的序列的长度很小的时候非常快)。然后我们将增量减小一般为 \(x = \frac{x}{2}\) (最后增量一定会变成 \(1\) ,所以是必然正确的),重复上面的步骤。虽然增量在变小,序列长度在增加,但会变得越来越有序,也就越来越高效。
又叫缩小增量排序。
最差时间复杂度:\(O(n(logn) ^ 2)\)
最优时间复杂度:\(O(n)\)
算法是否稳定:否
int ad=n/2;//增量一开始为n/2
while(ad>=1) {
for(int i=1;i<=ad;++i) {//分成ad组进行插入排序
for(int j=i+ad;j<=n;j+=ad) {//插入排序
int k=j-ad,temp=a[j];
while(k>=i&&a[k]>temp) {
a[k+ad]=a[k];k-=ad;
}
a[k+ad]=temp;
}
}
ad=ad/2;
}
之后可能会更新一下地精排序啥的,但之后再说。


