二进制详解 —— 从 18 元的生椰拿铁入手理解二进制
从日常生活中的十进制入手讲解二进制，图文并茂，并配有两道编程题。
本篇博文的 .md/html 文档和插图等文件都打包放在末尾的百度云链接[1]里了，我会根据博客实时更新的，有需要的伙伴可以自行下载~！
博文参考书籍：《明解C语言》[2]
二进制
为什么说从 18 元的生椰拿铁入手理解二进制呢？😂
因为 18 是我们日常生活中使用的十进制，而要理解二进制，要从十进制入手。
- 瑞幸的生椰拿铁18元。
- 这台电脑售价为5500元。
- 在聊天记录中搜索“你好”，找到了1条相关结果。
这些我们日常使用的数字都是十进制，数码为 0，1，2，3，4，5，6，7，8，9，运算规则为 “逢十进一，借一当十” 等等。不过，在计算机中所有数据都是用开关信号（1或0）来表示的，十进制对于我们来说更好理解，但对于计算机来说以 2 为基数的二进制更好理解。
学进制之前先来看几个概念：
- 数码：数中的每一位数字。例如十进制的数码是：0，1，2，3，4，5，6，7，8，9 ；二进制的数码是 0，1 。
- 基数：数码的个数，又是进位的基准。例如十进制的数码有 0~9 十个，所以是逢十进一；而二进制的数码有 0、1 两个，基数就为 2 。
- 位数：数码在这个数中的位置，从右开使从 0 递增。例如十进制数 1024 中 4 是第 0 位，2 是第 1 位，以此类推······那么在二进制数 00010000 中 1 是第 4 位。
- 位权：某一位上 “1” 表示的大小。例如在十进制数中：第 0 位数字的位权是 \(10^0\)，第 2 位数字的位权是 \(10^2\) 。在二进制数中：第 0 位数字的位权是 \(2^0\)，第 2 位数字的位权是 \(2^2\) 。
相信我，明晰这些概念以后，我们理解二进制就完成了 80%。😎
与整数之间的转换
二进制转化为十进制
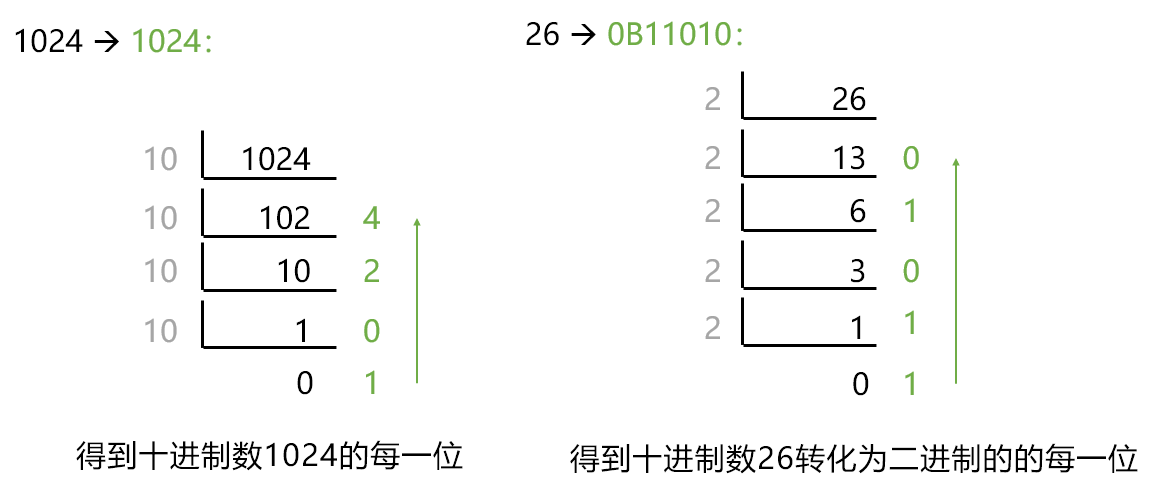
先拆个数，以 1024 为例：
所以，所有的十进制都可以由以上等式得到：每一位数字与该位位权的乘积之和等于十进制数。
将这个等式类比到二进制，就是如何将二进制数转化为十进制数的方法。
以0B11010为例：
- 为了区分二进制和十进制，通常会在二进制前加上0B（Binary），十进制前加上0D（Decimal），但由于十进制是日常最常表示的进制，所以0D可以省略。
十进制转化为二进制
如果给你一个十进制数，如何利用程序或者算法得到这个数的每一位？
这个问题是进制转化的核心。思路⬇️
一个数（以下不做特殊说明，均是十进制数）除基数 10 （与 10 取余）得到的余数是他的末尾数字。
以 1024 为例：
1024 % 10 = 4
再除以10就将这个数字执行了一次 ' 右移 ' 操作。
1024 / 10 = 102
重复以上运算（与 10 取余再除以 10）至除以 10 后的结果为 0，就得到了这个数的每一位。
1024 % 10 = 4 //第 0 位：4
1024 / 10 = 102
102 % 10 = 2 //第 1 位：2
102 / 10 = 10
10 % 10 = 0 //第 2 位：0
10 / 10 = 1
1 % 10 = 1 //第 3 位：1
1 / 10 = 0
类比到二进制，将十进制数不断与基数 2 取余，再与除以基数 2 右移，重复至运算结果为 0，就将这个十进制数转化成了二进制数。
以 26（0B11010）为例：
26 % 2 = 0 //第 0 位：0
26 / 2 = 13
13 % 2 = 1 //第 1 位：1
13 / 2 = 6
6 % 2 = 0 //第 2 位：0
6 / 2 = 3
3 % 2 = 1 //第 3 位：1
3 / 2 = 1
1 % 2 = 1 //第 4 位：1
1 / 2 = 0
画成图就是这样的⬇️
相信我，掌握这些以后，我们理解二进制就完成了 92%。😎
还有以这个为思路的两道编程题，为了不影响内容的连续性，放到文章末尾了。如果想现在做，点击此处跳转。
一个有趣的规律
在十进制中，能被 10 整除的数，有什么规律？
是的，以 0 结尾。比如 150，210······
能解释这个规律的角度有很多。从我的角度来看，每一个数码 9 + 1 后，都会由于超过最大数码（0 ~ 9），进位变成 '10'，从而能够被 10 整除。也就是说，超过 n 进制中（n=10）最大数码（9）一位后，会向前进 1，变成 '10'，成为能被 n 整除的数。
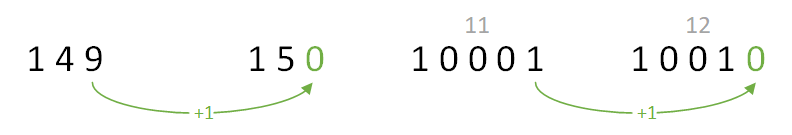
类比到二进制：能被 2 整除的数通常以 0 结尾，也是最大数码（1）加一后进位形成的，所以二进制的第零位如果是 0，则该数为偶数（如1010），是 1 则为奇数（如1011）。
这也常被用于验证一个数是奇数还是偶数：
if (n % 2)
puts("奇数");
else
puts("偶数");
与浮点数之间的转换
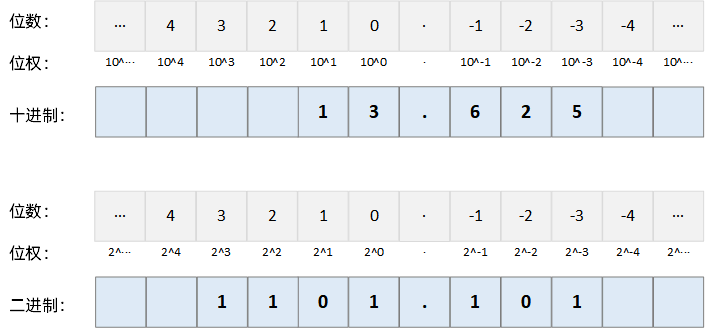
和前面相同，在十进制中，小数部分的每一位都有自己的位权（10 的指数幂），在小数点后从左向右依次是：\(10^{-1}\)，\(10^{-2}\)，\(10^{-3}\)，\(10^{-4}\)，\(10^{-5}\)······
那么，二进制也是一样的。在小数点后从左向右的位权依次是：\(2^{-1}\)，\(2^{-2}\)，\(2^{-3}\)，\(2^{-4}\)，\(2^{-5}\)······
以十进制数 13.625 和二进制数 1101.101 为例，位权和数字之间的关系如图：
二进制小数➡️十进制小数
因为一个浮点数可以拆分成整数 + 小数嘛，所以整数部分的转换仍旧按照上面的方式进行，主要是小数部分。不过小数转化成二进制依旧利用上文的等式转换，即每一位数字与该位位权的乘积之和等于十进制数。
以0B1101.101为例：
所以，0B1101.101就是十进制的 13.625。
十进制小数➡️二进制小数
十进制小数转换为二进制小数的方法和上面十进制转换成二进制的方式相同，只是把过程反过来再稍微稍微修改一下。
回想一下，十进制整数转换为二进制的方法，不断与 10 取余（拿走余数）再与 10 相除，至不能再这样计算（相除结果为 0）。
反过来，小数部分与 2 相乘（拿走乘积的整数位）再取走乘积的小数部分，重复此过程，至不能再这样计算（没有小数了），或者是达到了要求转换的精度，因为有些小数是不能完全转换成二进制的，他会无限循环下去，类似于十进制中的无限小数。
以 13.625 为例：
0.625 × 2 = 1.25 //第 -1 位：1
0.25 × 2 = 0.5 //第 -2 位：0
0.5 × 2 = 1.0 //第 -3 位：1
//小数为 0，已经不能再计算了，转换完毕
所以，13.625 就是二进制的0B1101.101。
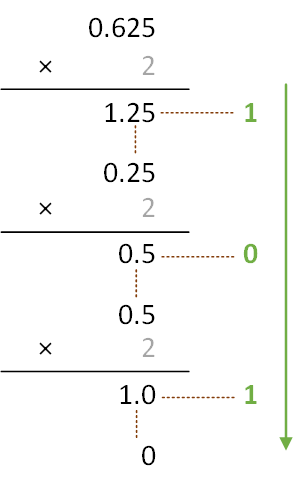
有些小数是不能完全转换的，因为这个数不能拆成位权的和，即 \(2^{-1}+2^{-2}+2^{-3}+···\) 这个形式。
例如：十进制数 0.1 = 0B00011001···
最后，二进制并不难，只是我们用惯了十进制，对其他进制的使用还不熟练。就像我有 12 杯生椰拿铁，一个袋子能装 10 杯，我就有两袋拿铁；一个袋子只能装 2 杯，我就有 6 袋；一袋能装 4 杯，我就有 3 袋 ······ 其实都是那一个数字，只是进制不同，表现出来的形式不同而已。再比如同样的意思，可以用汉语表达，也可以使用英语、法语或俄语。归根结底只是我们的工具罢了~!
【题目1】输入一个十进制，逆序输出它的二进制的每一位。
//输入：13
//输出：1 0 1 1
【答案】
int main()
{
int n = 0;
printf("Input:>"); //输入一个数
scanf("%d", &n);
for (; (unsigned int)n != 0; n /= 2)
printf("%d ", n % 2); //输出二进制的最后一位
return 0;
}
【题目2】输入一个十进制，按顺序输出它的二进制的每一位。
//输入：13
//输出：1 1 0 1
【答案】
unsigned int Fun(unsigned int n)
{
if (n)
Fun(n / 2); //数字不是 0 时，将其右移 1 位
else
return 0; //对应上文，运算结果为 0 时，函数返回 0
printf("%d ", n % 2); //输出二进制数的最后一位
}
int main()
{
int n = 0;
printf("Input:>"); //输入一个数
scanf("%d", &n);
Fun(n); //按顺序输出二进制的每一位
return 0;
}
百度网盘链接，点击下载 提取码：ztbu ↩︎
《明解C语言》入门篇 第 3 版 [日]柴田望洋 / 著 管杰 杜晓静 / 译 ↩︎
