机器视觉Day1 | 卡尔曼滤波、拟合、Apriltag、ARToolkit
拟合:
通过对点的拟合形成线、面。
-->常用方法
最小二乘法、梯度下降法、高斯牛顿(即迭代最小二乘法)、列-马算法。
-->分类
分为线性、非线性。非线性拟合常用多项式拟合
参考:
https://blog.csdn.net/weixin_60737527/article/details/123849242
——————————————————————————————
Apriltag:
AprilTag是一个视觉基准库,在AR,机器人,相机校准领域广泛使用。
通过特定的标志(与二维码相似,但是降低了复杂度以满足实时性要求),可以快速地检测标志,并计算相对位置。

官网:https://april.eecs.umich.edu/software/apriltag.html
——————————————————————————————
ARToolkit:
ARToolKit系统核心思路:
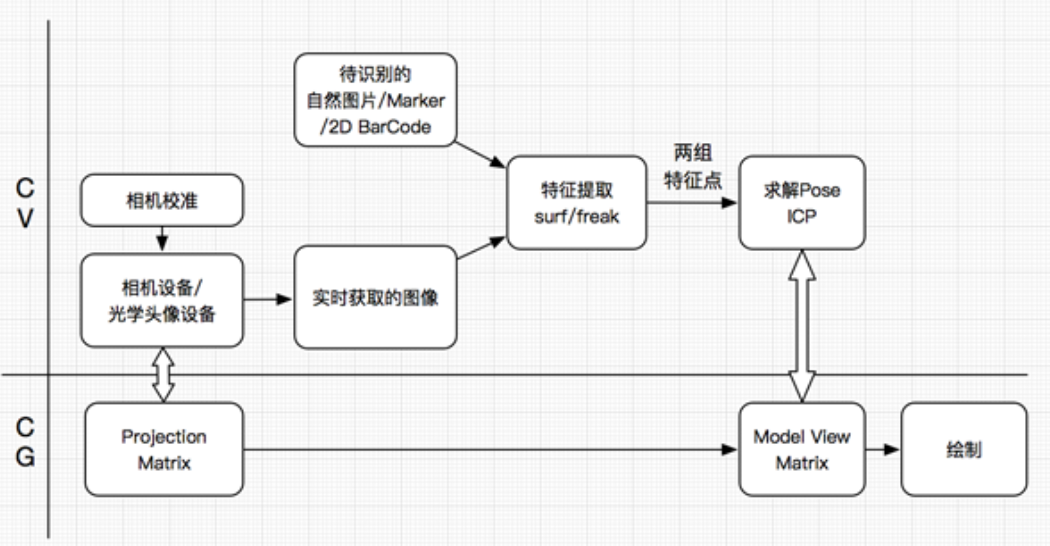
参考:https://www.cnblogs.com/polobymulberry/p/5857372.html
——————————————————————————————
卡尔曼滤波:
(通过预测进行目标追踪,增强鲁棒性,避免目标跟踪遗失的情况)
-适用于线性系统 高斯滤波环境(噪声高斯分布)-
-->现象视频:
-->扩展卡尔曼:
非线性to线性(泰勒展开 计算雅可比矩阵)
一、简介
卡尔曼滤波是一种估算系统状态的方法,它结合了系统的动态模型(即我们如何认为系统状态会随时间变化)和传感器的实际测量值。通过不断地预测和更新,卡尔曼滤波能够逐渐减小对系统状态估计的不确定性,从而得到更准确的估计结果。
二、流程
- 初始化:
设定一个初始的状态估计值(比如,您认为系统现在处于什么状态)。
设定一个初始的协方差矩阵(表示您对初始状态估计的不确定性有多大)。 - 预测:
使用系统的动态模型(可能是一个或多个数学方程),根据上一时刻的状态估计值,预测当前时刻的状态(尽管这只是一个猜测,但基于我们的模型)。
同时,更新协方差矩阵,以反映这个预测的不确定性(因为模型本身可能不准确,或者受到外部干扰)。 - 观测:
从传感器获取当前时刻的实际测量值。 - 更新:
比较预测值和测量值之间的差异(残差)。
使用这个残差来调整我们的预测值,得到一个更接近真实状态的新估计值(后验估计值)。
同时,更新协方差矩阵,以反映这个新估计值的不确定性(现在我们已经有了更多的信息,所以不确定性应该减小了)。 - 重复:
使用新的状态估计值和协方差矩阵,重复上述的预测和更新步骤,不断地逼近真实的系统状态。
三、核心方程
- 状态预测方程:告诉我们如何根据上一时刻的状态来预测当前时刻的状态。
- 协方差预测方程:告诉我们预测的不确定性有多大。
- 卡尔曼增益方程:是一个“权衡”因子,它决定了在更新过程中我们应该更相信预测值还是测量值。
- 状态更新方程:使用卡尔曼增益和测量残差来调整预测值,得到新的状态估计值。
- 协方差更新方程:更新我们对新状态估计值的不确定性。
四、教程:
五、python实现
NumPy库来实现的一维卡尔曼滤波
点击查看代码
import numpy as np
# 定义卡尔曼滤波的参数
# 状态转移矩阵
A = np.array([[1]])
# 控制矩阵(如果系统没有控制输入,则为0)
B = np.array([[0]])
# 观测矩阵
H = np.array([[1]])
# 过程噪声协方差
Q = np.array([[1e-5]])
# 观测噪声协方差
R = np.array([[1]])
# 初始状态估计
x_est = np.array([[0]])
# 初始误差协方差估计
P_est = np.array([[1]])
# 真实状态和观测数据(为了示例而模拟)
true_state = np.array([0.37])
measurements = np.array([0.39, 0.50, 0.48, 0.29, 0.25, 0.32, 0.34, 0.48, 0.41, 0.45])
# 卡尔曼滤波更新过程
estimates = []
for meas in measurements:
# 预测
x_pred = A @ x_est
P_pred = A @ P_est @ A.T + Q
# 更新
K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
x_est = x_pred + K @ (meas - H @ x_pred)
P_est = (np.eye(len(x_est)) - K @ H) @ P_pred
estimates.append(x_est[0,0])
# 输出结果
print(estimates)
二维滤波
点击查看代码
import numpy as np
class KalmanFilter:
def __init__(self, dt, process_variance, measurement_variance):
# 状态转移矩阵 A
self.A = np.array([[1, dt], [0, 1]])
# 观测矩阵 H
self.H = np.array([[1, 0], [0, 1]])
# 过程噪声协方差矩阵 Q
self.Q = np.array([[0.01, 0], [0, 0.01]]) * dt**2
# 观测噪声协方差矩阵 R
self.R = np.array([[measurement_variance, 0], [0, measurement_variance]])
# 初始状态估计 x
self.x = np.array([[0], [0]]) # 初始位置和速度
# 初始协方差矩阵 P
self.P = np.array([[1, 0], [0, 1]])
def predict(self):
# 预测下一个状态
self.x = np.dot(self.A, self.x)
# 更新协方差矩阵
self.P = np.dot(np.dot(self.A, self.P), self.A.T) + self.Q
def update(self, z):
# 计算卡尔曼增益
S = np.dot(np.dot(self.H, self.P), self.H.T) + self.R
K = np.dot(np.dot(self.P, self.H.T), np.linalg.inv(S))
# 更新状态估计
y = z - np.dot(self.H, self.x)
self.x = self.x + np.dot(K, y)
# 更新协方差矩阵
I = np.eye(len(self.x))
self.P = np.dot((I - np.dot(K, self.H)), self.P)
# 使用示例
dt = 0.1 # 时间间隔
process_variance = 0.1 # 过程噪声方差
measurement_variance = 1.0 # 观测噪声方差
kf = KalmanFilter(dt, process_variance, measurement_variance)
# 模拟一些观测数据
true_x = 0
true_y = 0
true_vx = 1
true_vy = 1
measurements = []
for _ in range(40):
true_x += true_vx * dt
true_y += true_vy * dt
# 添加一些噪声
z_x = true_x + np.random.normal(0, measurement_variance)
z_y = true_y + np.random.normal(0, measurement_variance)
measurements.append([z_x, z_y])
# 运行卡尔曼滤波器
estimated_positions = []
for z in measurements:
kf.predict()
kf.update(np.array(z).reshape(2, 1))
estimated_positions.append(kf.x.flatten().tolist())
# 输出结果(可选)
for pos in estimated_positions:
print(pos)
filterpy库实现
- filterpy是一个专门用于实现各种滤波算法的Python库,包括卡尔曼滤波、扩展卡尔曼滤波、无迹卡尔曼滤波等。使用filterpy可以大大简化卡尔曼滤波的实现过程。 -
点击查看代码
from filterpy.kalman import KalmanFilter
import numpy as np
# 初始化卡尔曼滤波器
kf = KalmanFilter(dim_x=1, dim_z=1)
kf.x = np.array([[0.]]) # 初始状态
kf.F = np.array([[1.]]) # 状态转移矩阵
kf.H = np.array([[1.]]) # 观测矩阵
kf.R = np.array([[1.]]) # 观测噪声协方差
kf.Q = np.array([[1e-5]]) # 过程噪声协方差
kf.P *= 1000. # 初始误差协方差矩阵,赋予较大值
# 真实状态和观测数据(为了示例而模拟)
measurements = np.array([0.39, 0.50, 0.48, 0.29, 0.25, 0.32, 0.34, 0.48, 0.41, 0.45])
estimates = []
for meas in measurements:
kf.predict()
kf.update(meas)
estimates.append(kf.x[0,0])
print(estimates)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号