堆排序

1.算法介绍

　　堆排序是一种树形选择排序，是对直接选择排序的有效改进。

　　堆实际上是一棵完全二叉树，其任何一非叶节点满足性质：Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]

　　即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。

　　堆分为大顶堆和小顶堆，满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆，满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。

　　由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。

2.算法原理

 利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

    其基本思想为(大顶堆)：

    1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

    2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

    操作过程如下：

     1)初始化堆：将R[1..n]构造为堆；

     2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

    因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

 

下面举例说明：

     给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

    首先根据该数组元素构建一个完全二叉树，得到

 

 然后需要构造初始堆，则从最后一个非叶节点开始调整，调整过程如下：

20和16交换后导致16不满足堆的性质，因此需重新调整

这样就得到了初始堆。

即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

此时3位于堆顶不满堆的性质，则需调整继续调整

 这样整个区间便已经有序了。

    从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

 

3.源代码

void print(int a[], int n){  
    for(int j= 0; j<n; j++){  
        cout<<a[j] <<"  ";  
    }  
    cout<<endl;  
}  
  
  
  
/** 
 * 已知H[s…m]除了H[s] 外均满足堆的定义 
 * 调整H[s],使其成为大顶堆.即将对第s个结点为根的子树筛选,  
 * 
 * @param H是待调整的堆数组 
 * @param s是待调整的数组元素的位置 
 * @param length是数组的长度 
 * 
 */  
void HeapAdjust(int H[],int s, int length)  
{  
    int tmp  = H[s];  
    int child = 2*s+1; //左孩子结点的位置。(i+1 为当前调整结点的右孩子结点的位置)  
    while (child < length) {  
        if(child+1 <length && H[child]<H[child+1]) { // 如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点)  
            ++child ;  
        }  
        if(H[s]<H[child]) {  // 如果较大的子结点大于父结点  
            H[s] = H[child]; // 那么把较大的子结点往上移动，替换它的父结点  
            s = child;       // 重新设置s ,即待调整的下一个结点的位置  
            child = 2*s+1;  
        }  else {            // 如果当前待调整结点大于它的左右孩子，则不需要调整，直接退出  
             break;  
        }  
        H[s] = tmp;         // 当前待调整的结点放到比其大的孩子结点位置上  
    }  
    print(H,length);  
}  
  
  
/** 
 * 初始堆进行调整 
 * 将H[0..length-1]建成堆 
 * 调整完之后第一个元素是序列的最小的元素 
 */  
void BuildingHeap(int H[], int length)  
{   
    //最后一个有孩子的节点的位置 i=  (length -1) / 2  
    for (int i = (length -1) / 2 ; i >= 0; --i)  
        HeapAdjust(H,i,length);  
}  
/** 
 * 堆排序算法 
 */  
void HeapSort(int H[],int length)  
{  
    //初始堆  
    BuildingHeap(H, length);  
    //从最后一个元素开始对序列进行调整  
    for (int i = length - 1; i > 0; --i)  
    {  
        //交换堆顶元素H[0]和堆中最后一个元素  
        int temp = H[i]; H[i] = H[0]; H[0] = temp;  
        //每次交换堆顶元素和堆中最后一个元素之后，都要对堆进行调整  
        HeapAdjust(H,0,i);  
  }  
}   
  
int main(){  
    int H[10] = {3,1,5,7,2,4,9,6,10,8};  
    cout<<"初始值：";  
    print(H,10);  
    HeapSort(H,10);  
    //selectSort(a, 8);  
    cout<<"结果：";  
    print(H,10);  
  
}  

4.时间复杂度

　　设树深度为k，。从根到叶的筛选，元素比较次数至多2(k-1)次，交换记录至多k 次。所以，在建好堆后，排序过程中的筛选次数不超过下式： 

                                

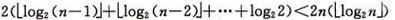
　　而建堆时的比较次数不超过4n 次，因此堆排序最坏情况下，时间复杂度也为：O(nlogn )。

 5.稳定性分析

 　　排序的稳定性是指如果在排序的序列中，存在前后相同的两个元素的话，排序前 和排序后他们的相对位置不发生变化，所以是不稳定的

 

 

注：参考链接http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html