kd树及python实现

kd树

实现k近邻时当训练数据量较大时，采用线性扫描法(将数据集中的数据与查询点逐个计算距离比对)会导致计算量大效率低下．这时可以利用数据本身蕴含的结构信息，构造数据索引进行快速匹配．索引树便是其中常用的一种方法．

kd树是其中一种索引树，是对k维空间中包含所有实例点进行划分以便进行快速匹配的一种数据结构．

给定一个二维数据集：[(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)]，构造一个平衡kd树．

特征空间划分：

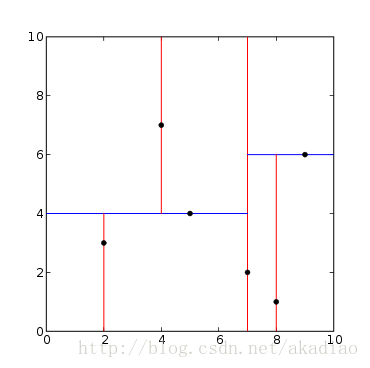
kd数示例：

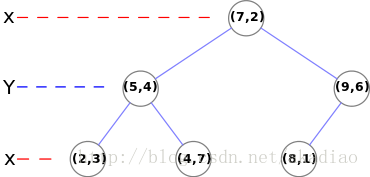
#!/usr/bin/python
# -*-coding:utf-8-*-

from collections import namedtuple
from operator import itemgetter
from pprint import pformat

# 节点类,（namedtuple）Node中包含样本点和左右叶子节点
class Node(namedtuple('Node', 'location left_child right_child')):
    def __repr__(self):
        return pformat(tuple(self))

# 构造kd树
def kdtree(point_list, depth=0):
    try:
        # 假设所有点都具有相同的维度
        k = len(point_list[0])
    # 如果不是point_list返回None
    except IndexError as e:
        return None
    # 根据深度选择轴，以便轴循环所有有效值
    axis = depth % k

    # 排序点列表并选择中位数作为主元素
    point_list.sort(key=itemgetter(axis))
    # 向下取整
    median = len(point_list) // 2

    # 创建节点并构建子树
    return Node(
        location=point_list[median],
        left_child=kdtree(point_list[:median], depth + 1),
        right_child=kdtree(point_list[median + 1:], depth + 1))

def main():
    point_list = [(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)]
    tree = kdtree(point_list)
    print(tree)

if __name__ == '__main__':
    main()

　

输出：

((7, 2),
 ((5, 4), ((2, 3), None, None), ((4, 7), None, None)),
 ((9, 6), ((8, 1), None, None), None))

#!/usr/bin/python
# -*-coding:utf-8-*-

import numpy as np
from sklearn.neighbors import KDTree

np.random.seed(0)
X = np.array([(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)])
tree = KDTree(X, leaf_size=2)
# ind：最近的3个邻居的索引
# dist：距离最近的3个邻居
# [X[2]]:搜索点
dist, ind = tree.query([X[2]], k=3)

print 'ind:',ind
print 'dist:',dist

　　

输出：

ind: [[2 1 5]]
dist: [[ 0.          4.47213595  4.47213595]]