用二分法确定蹦极运动员的体重(选修课大作业)

用二分法确定蹦极运动员的体重

目录

• 用二分法确定蹦极运动员的体重
  • 引言
  • 函数的建立
  • 二分法
  • 二分法的误差估计
  • MATLAB 的M文件：bisect

引言

医学研究表明，如果在自由下落4 s后自由落体速度超过了36 m/s，那么碰击运动员持续大幅振动损伤的概率会显著增加。蹦极运动公司的老板希望确定，在给定0.25 kg/m的阻力系数下超越该准测的蹦极运动员体重是多少。

---

函数的建立

我们知道可以运用如下解析解预测作为时间函数的下落速度：

\[v（t）=\sqrt{gm/c_d}*\tan(h)(\sqrt{gc_d/m}*t) \]

尽可能的尝试，但是无论如何也都无法将该方程变换为显式地表示m，也就是说，无法将质量单独分离出来放在方程的左边。

可以用另外一种方式看待这个问题，就是在方程的两边同时减去\(V(t)\),可以得到一个新函数：

\[f（m）=\sqrt{gm/c_d}*\tan(h)(\sqrt{gc_d/m}*t)-v(t) \]

---

二分法

二分法是增量搜索方法的一个变种，在增量搜索方法中，区间每次总是折半。如果一个函数的符号在一个区间上发生了变化，那么就计算改函数在区间中点处的值。然后，就可以确定根的位置位于符号发生改变的子区间内。这样该子区间就变为下一次迭代的区间。一直重复这个过程，直到根能够满足要求的精度为止。该方法的图形描述如图1所示。

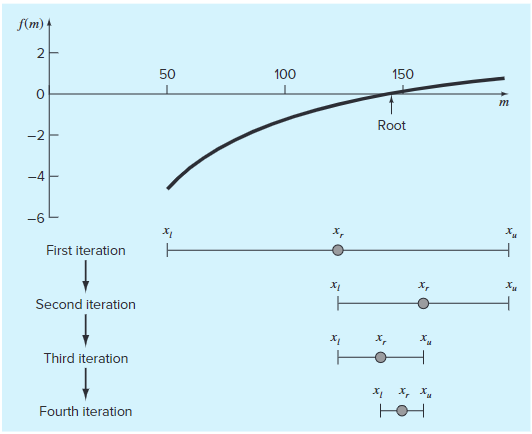
图1

---

二分法的第一步是猜测未知数（在本问题中的m）的两个值，要求它们能够使得\(f(m)\)具有不同的符号。易知，函数在50~200之间符号发生了变化。所以根的初始估计值为区间的中点：

\[x_r=(50+200)/2=125 \]

注意，通过其它方法我们预先计算出根的准确值为142.7376。这表明，经过1次迭代计算后得到的值，其真实百分比相对误差为：

\[|\xi_t|=|(142.7376-125)/142.7376|*100\%=12.43\% \]

接下来，计算函数在下界和中点处的值：

\[f(50)f(125)=-4.579(-0.409)=1.871 \]

结果大于0，在下界和中点之间没有发生符号变化。所以，根必定位于上半区间，即125~200之间，通过将下界定位于125,就创建了一个更加精确的新区间。

现在，新区间变为从x_t=125至x_u=200。然后就可以通过计算得到新根的估计值。例如：

\[x_r=(125+200)/2=162.5 \]

其真实百分比相对误差为\(\xi_t=13.85\%\). 可以重复这个过程以得到更精确的根的估计值。例如：

\[f(125)f(162.5)=-0.409(0.359)=-0.147 \]

所以，现在根位于下半区间，即125~162.5之间。上界精化为162.5，第3次迭代的根的估计只可以如下计算：

\[x_r=(125+162.5)/2=143.75 \]

其百分比相对误差为\(\xi_t=0.709\%\).可以重复该方法，直到结果的精度足够满足应用的需求为止。

---

二分法的误差估计

继续上文的计算过程，直到近似误差小于停止准则\(\xi_t=0.5\%\)为止。计算结果的误差。

得到迭代表（表1）如下

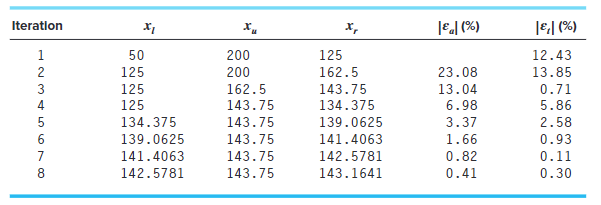
由此可以看出，在经过8次迭代以后，\(\xi_a\)最终小于\(\xi_s(\xi_s=0.5\%)\),计算过程可以结束。

在图2中对结果做了总结。真实误差“锯齿状”的特点是由于这样一个事实，即对于二分法，真实根可能位于划界区间中的任何地方。当真实根正好位于区间的中间时，真实误差与近似误差就相去甚远。当真实根靠近区间的两端时它们就很接近。

尽管近似误差无法给出真实误差的准确估计，但是图2表明，\(|\xi_a|\)与\(|\xi_t|\)向下的2总体趋势是吻合的。另外，该图还表现出了一个极具诱惑力的特点，就是\(|\xi_a|\)总是大于\(|\xi_t|\)。这样，但当\(|\xi_a |<|\xi_t |\)时，计算可以结束，并且得到的根至少要比和比预定可接受的精确度水平一样准确。

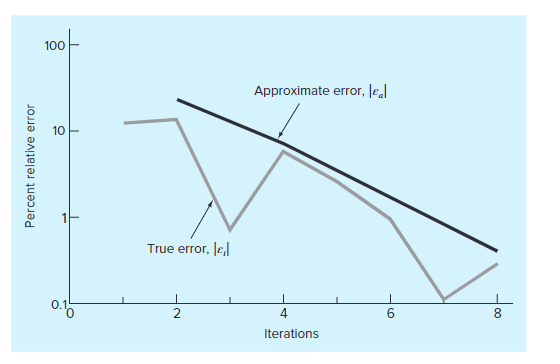
二分法的另一个优点是达到某个绝对误差所需的迭代次数可以预先计算得到，也就是说，在开始计算前就可以得到所需的迭代次数。如果\(E_{a,d}\)为预期误差，那么可以得到误差和迭代次数n的方程

\[n=\log_2 (\Delta x^0/E_{a,d}) \]

MATLAB 的M文件：bisect

下面给出了一个实现二分法的M文件。它需要传入函数（func）以及下界（xl）和上界（xu）的猜测值。另外，可以输入可选的停止准则（es），和最大迭代次数（maxit）。

function [root,fx,ea,iter]=QAQ(func,xl,xu,es,maxit,varargin)
% bisect: root location zeroes 
%   [root,fx,ea,iter]=bisect(func,xl,xu,es,maxit,p1,p2,...):
%       uses bisection method to find the root of func% input:
%   func = name of function
%   xl, xu = lower and upper guesses
%   es = desired relative error (default = 0.0001%)
%   maxit = maximum allowable iterations (default = 50)
%   p1,p2,... = additional parameters used by func% output:
%   root = real root
%   fx = function value at root
%   ea = approximate relative error (%)
%   iter = number of iterations

if nargin<3,error('at least 3 input arguments required'),end
test = func(xl,varargin{:})*func(xu,varargin{:});
if test>0,error('no sign change'),end
if nargin<4|isempty(es), es=0.0001;end
if nargin<5|isempty(maxit), maxit=50;end
iter = 0; xr = xl; ea = 100;
while (1)
  xrold = xr;
  xr = (xl + xu)/2;
  iter = iter + 1;
  if xr ~= 0;ea = abs((xr - xrold)/xr) * 100;end
  test = func(xl,varargin{:})*func(xr,varargin{:});
  if test < 0   
    xu = xr;
  elseif test > 0    
    xl = xr;  
  else    
    ea = 0; 
  end  
  if ea <= es | iter >= maxit,break,end
  end
  root = xr; fx = func(xr, varargin{:});

下面可以用该函数求解本章开头提出的问题。在给定0.25 kg/m的阻力系数的情况下，如果蹦极运动员自由下落4 s后的速度超过36 m/s，那么要求你确定蹦极运动员的体重。为此，必须求解下式的根：

\[f（m）=\sqrt{9.81m/0.25}*\tan(h)(\sqrt{9.81（0.25）/m}*4)-36 \]

使用下面的脚本，上述M文件中的bisect函数可以求解上式的根：

fm = @(m,cd,t,v) sqrt(9.81*m/cd)*tanh(sqrt(9.81*cd/m)*t) − v;

[mass fx ea iter] = bisect(@(m) fm(m,0.25,4,36),40,200)

由此可以看出，在进行21次迭代后，得到结果m=142.74 kg，其近似相对误差为\(\xi_a=0.00005345\%\),并且函数的值接近于0。