高斯消元学习笔记及算法实现与运用

0.前言

上大学了，好久没写博客了，刚好近期学习了高斯消元，打算在这篇文章中将知识点进行整理，同时对以前的OI知识进行一个复习。

1.高斯消元

阶梯形线性方程组

\[\left\{ \begin{aligned} a_ {1i_{1}}x_{i_{1}}+……+a_ {1i_{2}}x_{i_{2}}+……+a_ {1r_{1}}x_{1_{r}}+……a_ {1n}x_{n}=b_1\\ a_ {1i_{2}}x_{i_{2}}+……+a_ {2r_{1}}x_{2_{r}}+……a_ {2n}x_{n}=b_2 \\ …… \\ a_ {ri_{r}}x_{i_{1}}+……+ a_ {rn}x_{n}=b_r\\……\\0=b_{r+1}\\0=0\\……\\0=0\end{aligned} \right. \]

其中1=i₁<i₂<……<i_r\(\leq\)n, \(a_{ki_k}\neq0,k=1,2,……,r\),则称该线性方程组是阶梯形线性方程组。

Gauss消元法的基本思想可以描述为在不改变线性方程组解的前提下，将一般的线性方程组化为”阶梯形“线性方程组求解。其过程可以分为两步

消元过程
即将原线性方程组等价地化为接替形线性方程组；
回代过程
即从阶梯形线性方程组求得原线性方程组的解

线性方程组的解有3种情况

有唯一解
无解
有无穷解

线性方程组的初等变换（同解变换）

将线性方程组中某两个方程互换
将线性方程组中某个方程两边同时乘一个非零常数
将线性方程组中某个方程的k倍与另一个方程相加

两个定理

齐次线性方程组中，若方程个数s小于未知量个数n，则其必有非零解。
n元齐次线性方程组，只有零解的充分必要条件为线性方程组系数行列式不为零。

这里对第二个定理做证明

证明： 若线性方程组的系数行列式不为零，则由Cramer法则可知，线性方程组只有零解。

若线性方程组只有零解，则由Gauss消元法可知，消元过程结束时的阶梯形线性方程组为

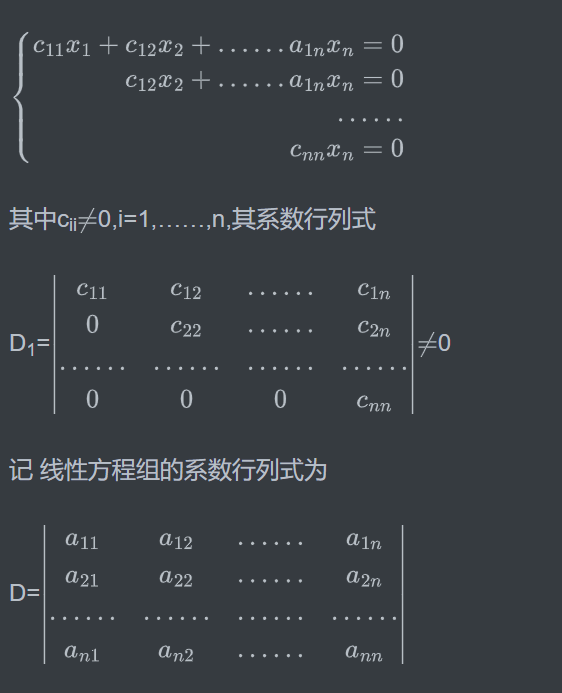
注意到阶梯形线性方程组是由线性方程组经过一系列初等变换所得，并且对方程组做初等变换时，发生变化的只是相应的方程中未知量前面的系数所以行列式D₁可以视为由行列式D经过一系列运算化为上三角形行列式而得，因此两者只差一个非零因子。由于D₁\(\neq0\)，故D\(\neq0\)，即线性方程组的系数行列式不为0.

阶梯形矩阵

若一个矩阵的零行（如果有的话）均在非零行的下方，并且每个非零行左起第一个非零元素所在的下标随着行标的增大而严格增大，则称次矩阵为阶梯形矩阵。如下：

\[\begin{bmatrix} 2&1&-1&8\\ 0&-1&2&11\\ 0&0&2&-1\\0&0&0&3\\0&0&0&0 \end{bmatrix}\]

这里给出一种更通俗的解释

\[\left\{ \begin{aligned} 非零行首个非零元素下方都是0\\ 零行在最下方 \end{aligned} \right. \]

2.算法实现

算法分析

如果给定一个形如以下式子得多元方程式

\[\left\{ \begin{aligned} 2x+y-z & = & 8 \\ -3x-y+2z& = &11 \\ -2x+y+2z & = & -1 \end{aligned} \right. \]

我们首先提出各项的系数（因为我们知道，高斯消元其实只跟系数有关）

我们可以写成一下矩阵形式

其中左边是各项的系数，最右边一列是等式右边的常数列

\[\begin{bmatrix} 2&1&-1&8\\ -3&-1&2&11\\ -2&1&2&-1\\ \end{bmatrix}\]

接下来我们进行加减消元

首先我们要用第i个方程来消去第k个方程的第k列，那么第k行所有元素A [ k ] [ j ]都应减去A [ i ] [ j ]的A [ k ] [ i ]/A [ i ] [ i ]倍。（我们约定，A [ i ] [ j ]是第i行第j列的系数）

上面的矩阵经过加减消元得

\[\begin{bmatrix} -3&-1&2&-11\\ 0&1/3&1/3&2/3\\ 0&5/3&2/3&13/3\\ \end{bmatrix}\]

接下来就是不断重复这个过程，再代入。

根据我们的算法，可以直接从最后一行推出X_n的值，然后倒数第二行可以推出X_n-1的值，以此类推。最后我们可以求出所有X的唯一解。

各部分代码详解

1.经过r行和第i行交换和加减消元

for(int i = 0; i < n; i ++) {
        r = i;
        for(int j = i + 1; j < n; j ++)
            if(fabs(A[j][i]) > fabs(A[r][i])) r = j; //fabs()表示计算浮点数的绝对值
        if(r != i) for(int j = 0; j <= n; j ++) std :: swap(A[r][j], A[i][j]);
       				/*↑↑      经过r行和第i行交换      ↑↑*/
                    
        for(int k = i + 1; k < n; k ++) {
			double f = A[k][i] / A[i][i];
			for(int j = i; j <= n; j ++) A[k][j] -= f * A[i][j];
		}            
        				/*↑↑     加减消元（低精度）    ↑↑*/
        
        for(int j = n; j >= i; j --) {
            for(int k = i + 1; k < n; k ++)
                A[k][j] -= A[k][i] / A[i][i] * A[i][j];
        }
        				/*↑↑     加减消元（保证精度）    ↑↑*/
    }

2.回代过程

	for(int i = n - 1; i >= 0; i --) {
		for(int j = i + 1; j < n; j ++)
			A[i][n] -= A[j][n] * A[i][j];
		A[i][n] /= A[i][i];
	}

总代码

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;

int n,m;
double a[110][110];


int main()
{
	scanf("%d",&n);
	m=n;
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n+1;j++)
		{
			scanf("%lf",&a[i][j]);
		}
	}
	int flag=0;
	for(int i=1;i<=n;i++)
	{
		int temp=i;
		while(a[temp][i]==0&&temp<=n)
		{
			temp++; 
		}
		if(temp==n+1)
		{
			flag=1;
			continue;
		}
		for(int j=1;j<=n+1;j++)
		{
			swap(a[i][j],a[temp][j]);
		}
		double k=a[i][i];
		for(int j=1;j<=n+1;j++)
		{
			a[i][j]/=k;
		}
		for(int j=1;j<=m;j++)
		{
			if(i!=j)
			{
				double k=a[j][i];
				for(int l=1;l<=n+1;l++)
				{
					a[j][l]-=(k*a[i][l]);
				}
			}
		}
	}
	if(flag)
	{
		printf("No Solution\n");
		return 0;
	}
	for(int j=1;j<=m;j++)
	{
		printf("%.2lf\n",a[j][n+1]/a[j][j]);
	}
	return 0;
}

3.高斯消元的实例运用

球形空间产生器（BZOJ1013）

有一个球形空间产生器能够在 n 维空间中产生一个坚硬的球体。现在，你被困在了这个 n 维球体中，你只知道球面上 n+1 个点的坐标，你需要以最快的速度确定这个 n 维球体的球心坐标，以便于摧毁这个球形空间产生器。数据保证有解，答案精确到小数点后三位。

一个球体上的所有点到球心的距离相等，因此只需求出一个点（x₁，x₂，……，x_n），使得：

\[\sum_{j=0}^n(a_i,_j-x_j)^2=C \]

其中C为常数，i属于[1,n+1],球面上第i个点的坐标为（a_i，1，a_i，2，……，a_i，n）。该方程组由n+1个n元二次方程构成，不是线性方程组。但是我们可以通过相邻两个方程做差，把它变成n个n元一次方程，同时消去常数C：

\[\sum_{j=1}^n(a_i,_j^2-a_i+_1,_j^2-2x_j(a_i,_j-a_i+_1,_j))=0 (i=1,2,…，n) \]

把变量放左边，把常数放右边：

\[\sum_{j=1}^n(a_i,_j^2-a_i+_1,_j^2)=\sum_{j=1}^n2x_j(a_i,_j-a_i+_1,_j) (i=1,2,…，n) \]

这就是一个线性方程组了。题目保证方程组有唯一解，我们直接对下面的增广矩阵进行高斯消元，变为简化阶梯形矩阵，即可得到每个x_j的值。

\[\begin{bmatrix} 2（a_1,_1-a_2,_1）&2（a_1,_2-a_2,_2）&……&2（a_1,_n-a_2,_n）&\sum_{j=1}^n(a_1,_j^2-a_2,_j^2)\\ 2（a_2,_1-a_3,_1）&2（a_2,_2-a_3,_2）&……&2（a_1,_n-a_2,_n）&\sum_{j=1}^n(a_1,_j^2-a_2,_j^2)\\ ……&……&……&……&……\\2（a_n,_1-a_n+_1,_1）&2（a_n,_2-a_n+_1,_2）&……&2（a_n,_n-a_n+_1,_n）&\sum_{j=1}^n(a_n,_j^2-a_n+_1,_j^2)\\\end{bmatrix}\]

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;

int n;
double a[20][20],b[20],c[20][20];



int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n+1;i++)
	{
		for(int j=1;j<=n;j++)
		{
			scanf("%lf",&a[i][j]);
		}
	 } 
	 for(int i=1;i<=n;i++)
	 {
	 	for(int j=1;j<=n;j++)
	 	{
	 		c[i][j]=2*(a[i][j]-a[i+1][j]);
	 		b[i]+=a[i][j]*a[i][j]-a[i+1][j]*a[i+1][j];
		 }
	 }
	 for(int i=1;i<=n;i++)
	 {
	 	for(int j=i;j<=n;j++)
	 	{
	 		if(fabs(c[i][j])>1e-8)
	 		{
	 			for(int k=1;k<=n;k++)
	 			{
	 				swap(c[i][k],c[j][k]);
				 }
				swap(b[i],b[j]);
			 }
		 }
		 for(int j=1;j<=n;j++)
		 {
		 	if(i==j) continue;
		 	double t=c[j][i]/c[i][i];
		 	for(int k=i;k<=n;k++)
		 	{
		 		c[j][k]-=t*c[i][k];
			}
			b[j]-=b[i]*t;
		 }
	 }
	 for(int i=1;i<=n;i++)
	 {
	 	printf("%.3lf ",b[i]/c[i][i]);
	 }
	return 0;
}

Barracuda（luoguP5027）

题目描述

大三角形给小正方形讲起自己的过去：过去的它是一个挖宝工，后来被黑暗之主污染才会落到此番境地。

它也希望小正方形去战胜黑暗之主，不过限于黑暗之主的眼线密布，因此必须给小正方形设置障碍才能骗过那些“眼线”。

他给小正方形的问题是：它有 n 个小三角形，每个小三角形有一定的质量，它对这些三角形进行了 n+1 次称量，然而由于托盘天平(?)的问题，有一次称量的结果是有误的。

现在，大三角形想要知道最重的小三角形的编号。

一组输入是合法的，当且仅当输入满足以下条件：

不存在一组 i,j，使得当我们假定第 i 条称量数据有误时能求出一种合法方案且我们假定第 j 条称量数据有误时也能求出一种合法方案。

合法方案定义如下：

1、最重的三角形只有一个。

2、不存在重量不确定的三角形。

3、所有三角形的重量均为正整数。

题目还是很好理解的，每次给定几个三角形和重量，就可以建立n+1个方程，转化为高斯消元模板

想一想高斯消元的模板长什么样子，一个n∗(n+1)的矩阵，但是按照上面的思路来建立的话，会搞出来一个(n+1)∗(n+1)的矩阵，那么就会遇到一些坑

思路就是假设每一行都是错误的情况

并不是每一个编号的系数为1，最开始我这里想了很久，可以抓多次同个三角形
如何假设是x*行出错，对于高斯消元时的处理，并不能直接continue当前行，还是应该存储一个模板矩阵

然后就继续说如何判断题目中的条件

最重的三角形只有一个，我们只需要在回代过后，对max x的个数记录一下即可
不存在重量不确定的三角形，说明该方程在转化为“上三角形”之后，出现了0=0这类恒等式，表示无数组解，当然无解也是这样
三角形重量是正整数，我们用double来存储答案，如果int强制转换后的值比double类型小，说明不是正整数
对于不是合法方案，其实就是相当于当i错误时，我们能求出来一组解,当jj错误时，我们也能求出来一组解，说明illegal

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const double eps=1e-6;
double a[150][150];
double b[150][150];
int n,m,x;
int maxx,pre;
int gauss() 
{
	int c,r;
	for(c=1,r=1; c<=n; c++) 
    {
		int t=r;
		for(int i=r; i<=n; i++) 
        {
			if(fabs(a[t][c])<fabs(a[i][c])) t=i;
		}
		if(fabs(a[t][c])<eps) return 0;
		for(int i=c; i<=n+1; i++) swap(a[r][i],a[t][i]);
		for(int i=n+1; i>=c; i--) a[r][i]/=a[r][c];
		for(int i=r+1; i<=n; i++) 
        {
			if(fabs(a[i][c])>eps) 
            {
				for(int j=n+1; j>=c; j--) a[i][j]-=a[r][j]*a[i][c];
			}
		}
		r++;
	} //高斯消元模板 
	for(int i=n; i>=1; i--) 
    {
		for(int j=i+1; j<=n; j++) 
        {
			a[i][n+1]-=a[j][n+1]*a[i][j];
		}
		if(a[i][n+1]<eps||((int)a[i][n+1])<a[i][n+1]) return 0; //无解或是重量为小数的情况 
	} //回代 
	int sum;
	maxx=-1;
	for(int i=1; i<=n; i++) 
	{
		if((int)a[i][n+1]>maxx) maxx=a[i][n+1],sum=i;
	} //记录最值 
	int num=0;
	for(int i=1; i<=n; i++)
	{
		if((int)a[i][n+1]==maxx) num++; //最值数量 
	}
	if(num>1) return 0;
	return sum;
}
int tot;
int main() 
{
	scanf("%d",&n);
	for(int i=1; i<=n+1; i++) 
	{
		scanf("%d",&m);
		for(int j=1; j<=m; j++) 
		{
			scanf("%d",&x);
			b[i][x]++;
		}
		scanf("%d",&x);
		b[i][n+1]=x*1.0;
	} //存储初始的(n+1)*(n+1)的矩阵 
	for(int i=1; i<=n+1; i++) 
	{
		int cnt=0;
		for(int h=1; h<=n+1; h++) 
		{
			if(h==i) continue;
			cnt++;
			for(int k=1; k<=n+1; k++) 
			{
				a[cnt][k]=b[h][k];
			}
		} //存储一个n*(n+1)的矩阵 
		int p=gauss();
		if(p==0) continue; //无解或者无数组解 
		else tot++,pre=p; //tot表示有几组解，pre是答案 
	}
	if(tot>1||tot==0) puts("illegal"); //全部无解或者出现多组解 
	else cout<<pre;  
	return 0;
}

4.如何理解Gauss消元法解线性方程组的正确性

线性方程组Ax=b求解的Gauss消元法就是将方程组的增广矩阵 \(\overline{A}\)=(A,b)作初等行变换化为阶梯形\(\overline{C}\)=(C,b)，然后再求解方程Cx=d，从而得到原方程组解的方法。在这个过程中我们既没验证方程组Cx=d的解就是Ax=b的解，又没证明求解过程中方程组的解会不会丢失。换句话说，为什么说方程组Cx=d和Ax=b一定同解？这个问题用方程组的向量形式来描述就会看得清楚。

首先将方程组Ax=b写成向量形式，记A=（\(\alpha\)₁,\(\alpha\)₂,……,\(\alpha\)_n）,其中\(\alpha\)_i=（a_1i,a_2i,……,a_mi）^T (i=1,2,……，n),则方程组可写成

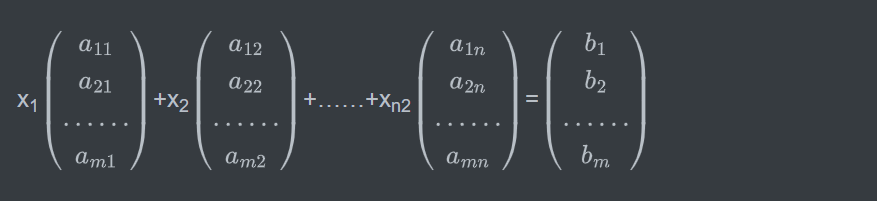
容易看出，对\(\overline{A}\)=(A,b)作初等变换等价于对方程组中的方程做相应的运算，这些运算不会改变上式中各列向量的线性关系。也就是各列向量的系数x₁，x₂,……,x_n与初等变换无关。另一方面，初等变换是可逆的，从而方程组Ax=b与Cx=b在初等行变换下可以互化，所以它们是同解的。

5.后记

这篇文章只是本人对于高斯消元的一些小小的思考总结，很多知识我也只是”知其然而不知其所以然“。我也再次意识到，在前人的伟大发现和思考前，我是多么渺小。如果本文有什么错误请正在阅读的您指出并告知，便于本人修改，也希望您能愿意和我交流学习相关知识。同时万分感激您能读到这里。

PS.

十分感谢我的同学，徐同学，愿意将她的笔记给我作为参考，她的帮助是我能完成此文的重要因素。

posted @ 2021-11-11 15:28 plzplz 阅读(684) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

plzplz

二人知ること孤独に同じ

高斯消元学习笔记及算法实现与运用

高斯消元学习笔记及算法实现与运用

0.前言

1.高斯消元

阶梯形线性方程组

线性方程组的初等变换（同解变换）

两个定理

阶梯形矩阵

2.算法实现

算法分析

各部分代码详解

1.经过r行和第i行交换和加减消元

2.回代过程

总代码

3.高斯消元的实例运用

球形空间产生器（BZOJ1013）

Barracuda（luoguP5027）

题目描述

4.如何理解Gauss消元法解线性方程组的正确性

5.后记

PS.

公告