透视投影矩阵
透视投影

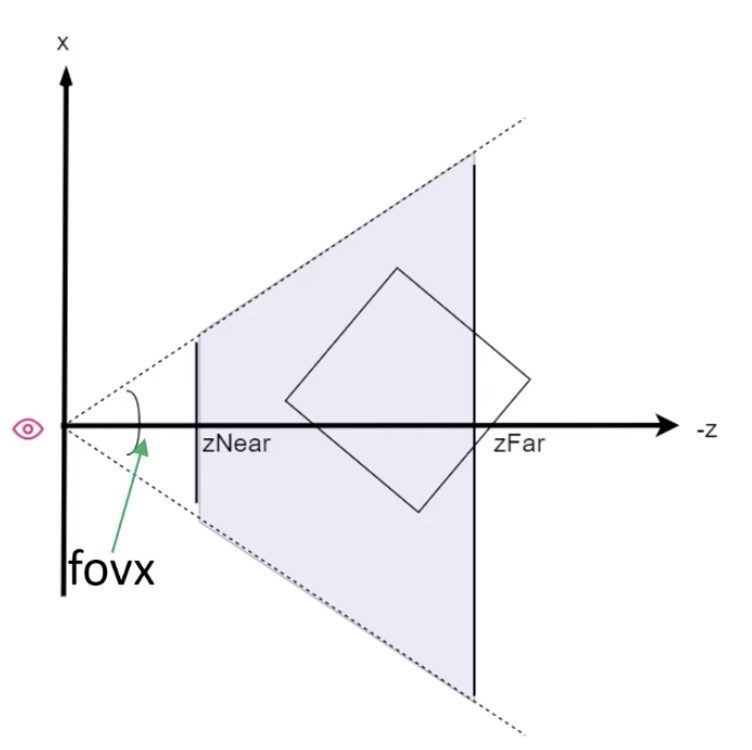
1. 将投影面上x,y,z方向上的点,投影到剪裁空间有一定比例关系
2. y方向上的比例关系
y/y0 = y'
y0/-z = tan(fov/2)
y' = y / tan(fov/2)*-z
让f=1/tan(fov/2)
y' = f/-z * y
3. x方向上的比例关系
x' = f'/-z * x
根据相似三角形原理:
tan(fovx/2)/tan(fovy/2)=f/f' = aspect = width/height
所以:
x' = f/aspect * 1/-z * x
4. 为了让z方向近大远小表示更真实,用双曲线来求z方向上的点
因为zFar = 1 zNear = -1
1 = m/zFar + c
-1 = m/zNear + c
解方程得到:
m = -(2 * zFar * zNear / zNear - zFar)
c = -(zFar + zNear/zNear-zFar)
令zNear = n, zFar = f
z' = 2nf/n-f * 1/-z - n+f/n-f
5. 将x',y',z'写成矩阵的形式
x' = f/aspect * 1/-z * x
y' = f/-z * y
z' = 2nf/n-f * 1/-z - n+f/n-f
f = 1/tan(fov/2)
让图形引擎去除以1/-z,所以消去1/-z
x'' = x'/-z
y'' = y'/-z
z'' = z'/-z
x'' = f/aspect * x
y'' = fy
z'' = 2nf/n-f + n+f/n-f *
A = [
f/aspect 0 0 0
0 f 0 0
0 0 n+f/n-f 2nf/n-f
0 0 -1 0
]
B = [
x
y
z
1
]
将w分量设置为-z,图形引擎计算的时候会将x,y,z各分量除以-z
A * B =
[
fx/aspect
fy
n+f/n-f + 2nf/n-f
-z
]
const m4 = {
perspective: function(fieldOfViewInRadians, aspect, near, far) {
const f = Math.tan(Math.PI * 0.5 - 0.5 * fieldOfViewInRadians);
var rangeInv = 1.0 / (near - far);
return [
f / aspect, 0, 0, 0,
0, f, 0, 0,
0, 0, (near + far) * rangeInv, -1,
0, 0, near * far * rangeInv * 2, 0
];
},


 浙公网安备 33010602011771号
浙公网安备 33010602011771号