视图变换
观察坐标系
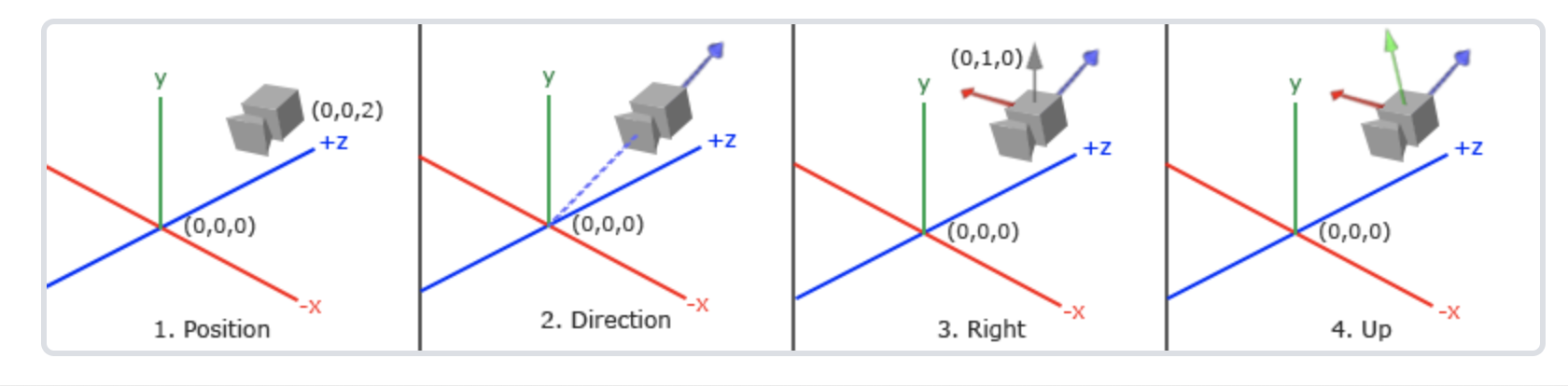
1. 定义摄像机的位置
const cameraPosition = new Vector3(0,0,10)
2. 指定摄像机的方向
// 摄像机看向坐标原点
const cameraTarget = new Vector3(0,0,0)
// 用场景原点方向减去摄像机位置向量得到的结果就是摄像机指向的向量。将向个向量互换位置得到一个指向摄像机z轴正方向的向量
const cameraDirection = normalize(cameraPosition - cameraTarget)
3. 指定右轴,代表摄像空间x轴的正方向,定义一个上向量将方向向量叉乘,得到指向x轴正方向的那个向量
const up = new Vector3(0,0,0)
const cameraRight = normalize(cross(up, cameraDirection))
4. 上轴,获取一个指向摄像机正y轴向量,右方向向量与方向向量进行叉乘
const cameraUp = cross(cameraDirection,cameraRight)
lookat(观察矩阵)
现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标,我们可以创建我们自己的LookAt矩阵了:注意,位置向量是相反的,因为我们最终希望把世界平移到与我们自身移动的相反方向。把这个LookAt矩阵作为观察矩阵可以很高效地把所有世界坐标变换到刚刚定义的观察空间。LookAt矩阵就像它的名字表达的那样:它会创建一个看着(Look at)给定目标的观察矩阵。
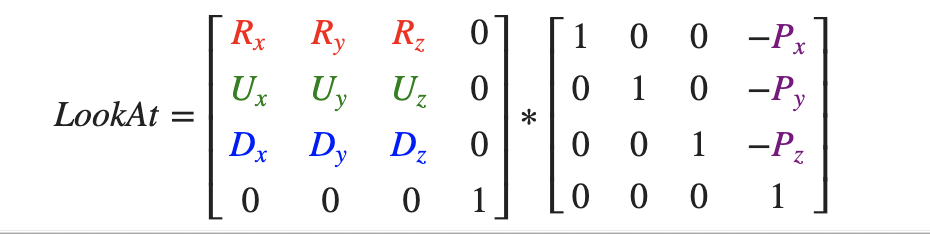
var m4 = {
lookAt: function(cameraPosition, target, up) {
var zAxis = normalize(
subtractVectors(cameraPosition, target));
var xAxis = normalize(cross(up, zAxis));
var yAxis = normalize(cross(zAxis, xAxis));
return [
xAxis[0], xAxis[1], xAxis[2], 0,
yAxis[0], yAxis[1], yAxis[2], 0,
zAxis[0], zAxis[1], zAxis[2], 0,
cameraPosition[0],
cameraPosition[1],
cameraPosition[2],
1,
];
}
视图矩阵
将观察矩阵求逆得到视图矩阵
假设有一顶点在坐标系A中坐标 P0,经过矩阵变换 M 后顶点在坐标系 B 中的坐标 P1,
P1 = M x P0
又有
M x M^-1 = I
I x P1 = P1
所以
M x M^-1 x P1 = M x P0
两边约去 M,可得
M^-1 x P1 = P0
顶点 P1 经过矩阵 M 的逆矩阵就可以变换回顶点 P0
// 计算第一个 F 的位置
var fPosition = [radius, 0, 0];
// 计算相机在圆上的位置矩阵
var cameraMatrix = m4.yRotation(cameraAngleRadians);
cameraMatrix = m4.translate(cameraMatrix, 0, 0, radius * 1.5);
// 获得矩阵中相机的位置
var cameraPosition = [
cameraMatrix[12],
cameraMatrix[13],
cameraMatrix[14],
];
var up = [0, 1, 0];
// 计算相机的朝向矩阵
var cameraMatrix = m4.lookAt(cameraPosition, fPosition, up);
// 通过相机矩阵获得视图矩阵
var viewMatrix = m4.inverse(cameraMatrix);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号