朴素匹配算法
//S 主串 T 模式串
//匹配失败,回溯
i = i - j + 1
j = 0
//匹配成功,返回位置
i - j
function indexOf(S,T,pos = 0){
let i = pos
let j = 0;
while(i <= S.length && j <= T.length){
if(S[i] == T[j]){
++i
++j
}else{
//回溯
i = i - j + 1
j = 0
}
}
if(j >= T.length){
return i - j
} else {
return 0
}
}
KMP算法
字符串前后缀
![image]()
![image]()
字符关系
A B C A B B
0 k-1 k j-k j-1 j
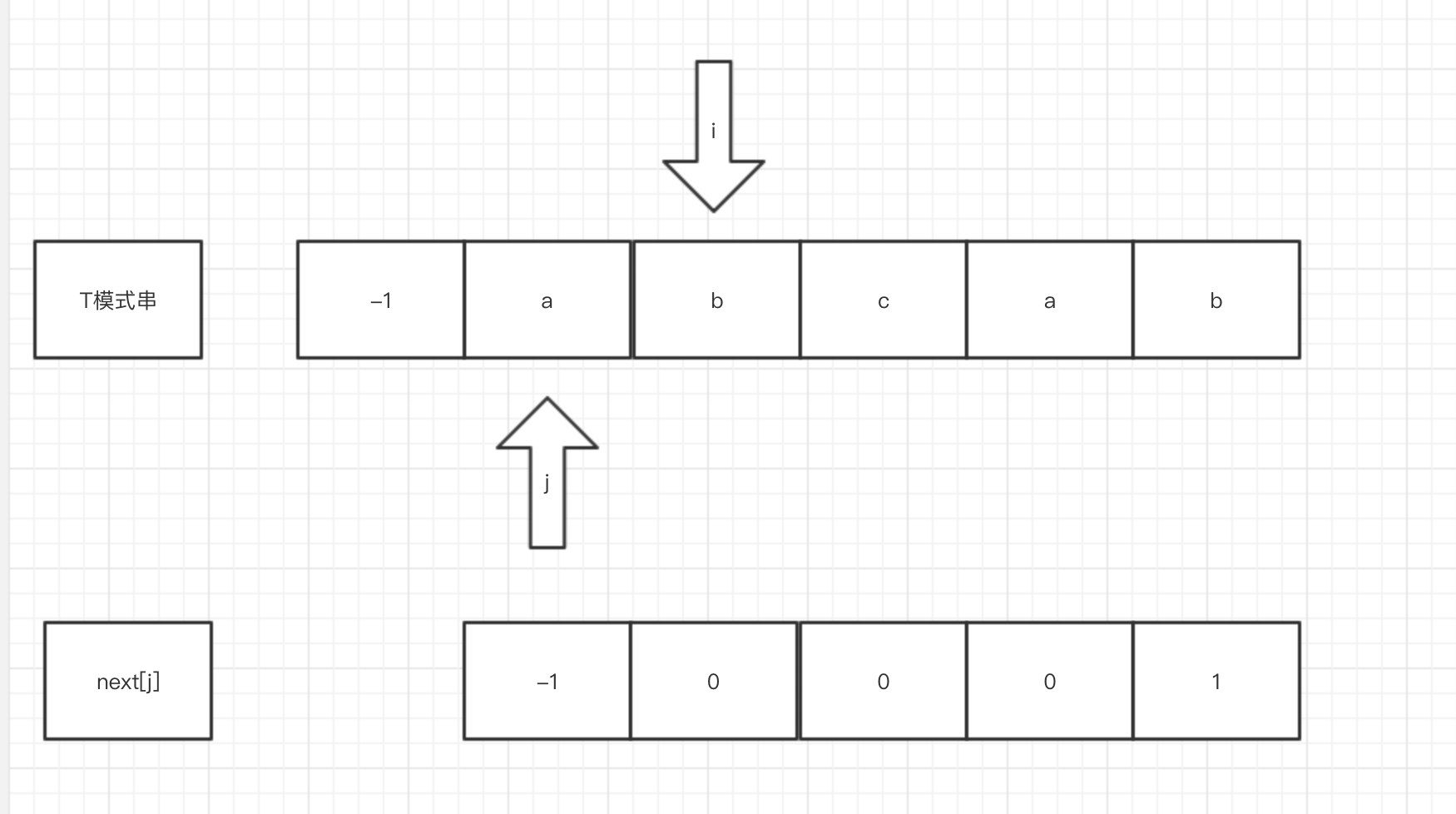
执行过程
![]()
//i指针不必回溯
//next[j]表示回溯位置
/*
规则1:没有公共前后缀的情况,匹配失败时j = 0去匹配
s: a b (c) d e f g
t: a b (d)
t串中a与后边的bd串都不相等,在d匹配c失败时,可以知道t[a] = s[a], t[b] = s[b],t[a] != t[b],因此t[a] != s[b]
因为t[a] != t[b] != s[b],所以不用比较t[a]与s[b],只需要将a移动到匹配失败的位置即可
s: a b (c) d e f g
t: (a) b d
规则2:有公共前后缀的情况,匹配失败时j 根据当前字符串的前后缀相似度进行匹配
s: a b c a b a b c a
t: a b c a b x
因为t[a] != t[b] != s[b] != s[c],所以匹配失败时不必比较s[b],s[c]
s: a b c a b a b c a
t: a b c a b x
因为t[0],t[1] = t[3],t[4],由于t[3],t[4] = s[3],s[4] = t[0],t[1],所以也s[3],s[4]也不用比较
在于s串比较时,都是通过判断t串中有无重复的元素,来决定与s串的某一位置进行比较
next[j] = {
0,当j = 1时,next[j] = 0
Max:{k | 1 < k < j, 且 p1 - pk-1 = pj-k+1 - pj - 1}
1,其他情况
}
现在的问题转移到当匹配失败时,如何计算出j的回溯位置 ?
k值就是公共前后缀的长度,如果k = 1,那么就是k + 1 = 2
t = abcdex
n = next[j]
j: 1 2 3 4 5 6
t: a b c d e x
n: 0 1 1 1 1 1
j = 1,j是a,没有前后缀,next[1] = 0
j = 2,j是ab,1 到 j - 1时,只有字符a,没有公共前后缀,next[2] = 1
j = 3,j是abc,1 到 j - 1,没有公共前后缀,next[3] = 1
j = 4,j是abcd,1 到 j - 1 没有公共前后缀,next[4] = 1
最后结果:next[j] = [0,1,1,1,1,1]
当匹配失败时,调用next[j],假设现在时j = 6匹配失败了,next[6] = 1, 那么我们应该回溯到j = 1 进行匹配,也就是t[1] = a
当有公共前后缀的情况
t = abcabx
n = next[j]
j: 1 2 3 4 5 6
t: a b c a b x
n: 0 1 1 1 2 3
j = 1,next[1] = 0
j = 2,1 到 j - 1的字符是a,next[2] = 1
j = 3,1 到 j - 1的字符是ab,next[3] = 1
j = 4,1 到 j - 1的字符是abc,next[4] = 1
j = 5,1 到 j - 1的字符是abca, 公共前后缀是a,next[5] = 2
j = 6, 1 到 j - 1的字符是abcab,公共前后缀是ab,next[6] = 3
当匹配失败时,j = 6,next[6] = 3,那么j回溯3去比较
j: 1 2 3 4 5 6 7 8 9
t: a b a b a a a b a
n: 0 1 1 2 3 4 2 2 3
当j = 1, next[1] = 0
当j = 2, next[2] = 1
当j = 3, next[3] = 1
当j = 4, 公共前后缀a,next[4] = 2
当j = 5,公共前后缀ab,next[5] = 3
当j = 6,公共前后缀aba,next[6] = 4
当j = 7,公共前后缀a,next[a] = 2
当j = 8,公共前后缀a,next[a] = 2
当j = 9,公共前后缀ab,next[a] = 3
当j = 9匹配失败时,next(9) = 3,j应该回溯到第j = 3的位置进行比较
j: 1 2 3 4 5 6 7 8 9
t: a a a a a a a a b
n: 0 1 2 3 4 5 6 7 8
j = 1, next[1] = 0
j = 2, next[2] = 1
j = 3, next[3] = 2
j = 4, next[4] = 3
j = 5, next[5] = 4
j = 6, next[6] = 5
j = 7, next[7] = 6
j = 8, next[8] = 7
j = 9, next[9] = 8
*/
function get_next(T,next = []){
let i = 0;
let j = -1;
//第一个字符就匹配失败的情况
next[0] = -1;
while(i < T.length - 1){
//假设没有前后缀,设置初始值,第二次循环在验证是不是真的没有前后缀
if(j == -1 || T[i] == T[j]){
//给没有公共前后缀和前后缀一致的字符添加回退索引
++i
++j
next[i] = j
}
else {
//根据失败位置索引,找到应该回退的索引
j = next[j]
}
}
return next
}
//进行修正
// s: aab
// t: aaa
//当a与b不匹配时,前面的a与后面的a是一样的没有必要在进行匹配
function get_nextval(T,nextval = []){
let i = 1;
nextval[1] = 0;
let j = 0;
while(i < T.length - 1){
if(j == -1 || T[i] == T[j]){
++i
++j
if(T[i] != T[j]){
nextval[i] = j
} else {
//如果前后缀相同的情况
//跳过层层回溯,直接回溯到开始位置
nextval[i] = nextval[j]
}
} else {
j = nextval[j]
}
}
}
function kmp_search(S,T,pos = 0){
let i = pos;
let j = 0;
let next = get_next(T)
console.log(next)
while( i < S.length && j < T.length){
if(j === -1 || S[i] === T[j]){
//j === -1 的时候将i向后移动的同时将j归0
i++
j++
} else {
j = next[j]
}
}
if(j === T.length){
return i - j
}
else {
return -1
}
}
//kmp另一种实现
function prefix_table(pattern = [],prefix = [],n){
pattern[0] = 0
let len = 0
let i
while( i < n){
if(pattern[i] == pattern[len]){
len ++
prefix[i] = len
i ++
}
else {
if(len > 0){
len = prefix[len - 1]
} else {
prefix[i] = len
i ++
}
}
}
}
function move_prefix_table(prefix = [],n){
let i
for(i = n - 1; i > 0; i--){
prefix[i] = prefix[i - 1]
}
prefix[0] = -1
}
function kmp_search(text = [],pattern = []){
let n = pattern.length
let m = text.length
let prefix = []
let i = 0
let j = 0
prefix_table(pattern,prefix,n)
move_prefix_table(prefix,n)
while( i < m){
if( j == n - 1 && text[i] == pattenr[j]){
console.log(i - j)
j = prefix[j]
}
if(text[i] == pattern[j]){
i++
j++
}
else {
j = prefix[j]
if(j == -1){
i++
j++
}
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号