math
1、UVa 11806
题意：在m*n的网格中放k个石子，每格最多放一个，且第一行，最后一行，第一列，最后一列均有石子，求放的方法总数。
解法：首先发现，如果题目要求第一行，最后一行，第一列，最后一列没有石子，那题目非常简单。
那么，用容斥原理。S表示全集，A，B分别表示第一行和最后一行没有石子，C，D分别表示第一列和最后一列没有石子，则所求为“在S中但不在A，B，C，D中”的集合的元素个数。
自己写的代码挺搓的- -，看了刘汝佳用2进制数写的代码后，也模仿了一下。
tag:math, 计数, 容斥原理
1 /* 2 * Author: plum rain 3 * Created Time: 2013-08-14 23:54 4 * File Name: 5 */ 6 #include<iostream> 7 #include<sstream> 8 #include<fstream> 9 #include<vector> 10 #include<list> 11 #include<deque> 12 #include<queue> 13 #include<stack> 14 #include<map> 15 #include<set> 16 #include<bitset> 17 #include<algorithm> 18 #include<cstdio> 19 #include<cstdlib> 20 #include<cstring> 21 #include<cctype> 22 #include<cmath> 23 #include<ctime> 24 #include<utility> 25 26 using namespace std; 27 28 #define CLR(x) memset(x, 0, sizeof(x)) 29 #define PB push_back 30 #define SZ(v) ((int)(v).size()) 31 #define INF 999999999999 32 #define zero(x) (((x)>0?(x):-(x))<eps) 33 #define out(x) cout<<#x<<":"<<(x)<<endl 34 #define tst(a) cout<<#a<<endl 35 #define CINBEQUICKER std::ios::sync_with_stdio(false) 36 37 typedef vector<int> VI; 38 typedef vector<string> VS; 39 typedef vector<double> VD; 40 typedef long long int64; 41 42 const double eps = 1e-8; 43 const double PI = atan(1.0)*4; 44 const int maxint = 2139062143; 45 const int MAX = 500; 46 const int mod = 1000007; 47 48 inline int Mymod( int a , int b ) { int x=a%b;if(x<0) x+=b;return x;} 49 50 int C[MAX+10][MAX+10]; 51 52 void Cinit() 53 { 54 CLR (C); 55 C[0][0] = 1; 56 for (int i = 0; i <= MAX; ++ i){ 57 C[i][0] = C[i][i] = 1; 58 for (int j = 1; j < i; ++ j) 59 C[i][j] = (C[i-1][j] + C[i-1][j-1]) % mod; 60 } 61 } 62 63 int main() 64 { 65 // freopen("a.in","r",stdin); 66 // freopen("a.out","w",stdout); 67 // std::ios::sync_with_stdio(false); 68 Cinit(); 69 70 int T; 71 scanf ("%d", &T); 72 int test = 0; 73 while (T--){ 74 int n, m, k; 75 scanf ("%d%d%d", &n, &m, &k); 76 77 int sum = 0; 78 for (int sta = 0; sta < 16; ++ sta){ 79 int num = 0, nn = n, mm = m; 80 if (sta&1) 81 ++ num, -- nn; 82 if (sta&2) 83 ++ num, -- nn; 84 if (sta&4) 85 ++ num, -- mm; 86 if (sta&8) 87 ++ num, -- mm; 88 int tmp = C[mm*nn][k]; 89 if (num&1) tmp *= -1; 90 sum = (sum + mod + tmp) % mod; 91 } 92 93 printf ("Case %d: %d\n", ++test, sum); 94 } 95 return 0; 96 }
2、World Finals 2008, LA 4123
题意：对一个边平行于坐标轴的多边形，从某个顶点开始按照逆时针顺序走，碰到一个90度的内角记R，碰到一个270度的内角记O，最后得到一串序列称角度序列。给定正整数n，有多少个长度为n的角度序列可以对应至少一个星形多边形（即多边形中存在一个点可以看到多边形边界上上每一点）？多边形长度任意。注意，一个多边形有可能有多个角度序列与之对应，如下图Figure 2可以对应RRORRORRORRO, ORRORRORRORR。(1 <= N <= 1000)
解法：首先，不难发现多边形顶点数即为角度序列长度。其次，要观察到n为奇数或n < 3时答案为0，否则角度序列一定有(n + 4) / 2个 R 和 (n - 4) / 2个 O。
然后，再发现(- -)可能会出现子序列RR，但一定不会出现OO，否则不为星形三角形。另一方面，只要是 R 比 O 多4个，且没有两个O相邻，一定可以构造出上述的星形多边形。
这样，题目就转化为把用(n+4) / 2个 R 和 (n - 4) / 2个 O 组成的，没有两个O相邻且不能首尾均为O(此情况等价于相邻，因为多边形等价与环)的序列的个数。答案C((n+4)/2, (n-4)/2)) + C((n+4)/2 - 1, (n-4)/2) - 1)。
tag:math, think, 计数
1 /* 2 * Author: plum rain 3 * Created Time: 2013-08-19 10:39 4 * File Name: math-LA-4123.cpp 5 */ 6 #include<iostream> 7 #include<sstream> 8 #include<fstream> 9 #include<vector> 10 #include<list> 11 #include<deque> 12 #include<queue> 13 #include<stack> 14 #include<map> 15 #include<set> 16 #include<bitset> 17 #include<algorithm> 18 #include<cstdio> 19 #include<cstdlib> 20 #include<cstring> 21 #include<cctype> 22 #include<cmath> 23 #include<ctime> 24 #include<utility> 25 26 using namespace std; 27 28 #define CLR(x) memset(x, 0, sizeof(x)) 29 #define PB push_back 30 #define SZ(v) ((int)(v).size()) 31 #define INF 999999999999 32 #define zero(x) (((x)>0?(x):-(x))<eps) 33 #define out(x) cout<<#x<<":"<<(x)<<endl 34 #define tst(a) cout<<#a<<endl 35 #define CINBEQUICKER std::ios::sync_with_stdio(false) 36 37 typedef vector<int> VI; 38 typedef vector<string> VS; 39 typedef vector<double> VD; 40 typedef long long int64; 41 42 const double eps = 1e-8; 43 const double PI = atan(1.0)*4; 44 const int maxint = 2139062143; 45 46 inline int Mymod( int a , int b ) { int x=a%b;if(x<0) x+=b;return x;} 47 48 int64 min(int64 a, int64 b) 49 { 50 return a < b? a: b; 51 } 52 53 int64 C(int64 y, int64 x) 54 { 55 if (y < x) return 0; 56 x = min (x, y-x); 57 58 int64 ret = 1; 59 for (int64 i = y, j = 1; i > y - x; -- i, ++ j) 60 ret = (ret * i) / j; 61 return ret; 62 } 63 64 int main() 65 { 66 // freopen("a.in","r",stdin); 67 // freopen("a.out","w",stdout); 68 // std::ios::sync_with_stdio(false); 69 int n, test = 0; 70 while (scanf ("%d", &n) != EOF && n){ 71 printf ("Case %d: ", ++ test); 72 if (n&1 || n == 2) printf ("0\n"); 73 else if (n == 4) printf ("1\n"); 74 else{ 75 int r = (n + 4) / 2, o = (n - 4) / 2; 76 cout << C((int64)r, (int64)o) + C((int64)(r-1), (int64)(o-1))<< endl; 77 } 78 } 79 return 0; 80 }
Ps: 星形多边形的判定参见http://madongfly.bokee.com/18473335.html(与本题无关)
3、UVa 11361
题意：给出整数a, b, k。求区间[a, b]中的数有多少个本身既是k的倍数，各位数字之和也是mod的倍数。(1 <= a <= b < 2^31, 1 <= k < 10000)
类似POJ 3286，本文第七题。
解法：首先构造函数x(n)表示小于等于n的数中符合题意的数的个数，则答案为f(b) - f(a-1)。
考虑求x(n)。假设n = 234，则f(n)的值为0**, 1**, 20*, 21*, 22*, 230, 231, 232, 233, 234中满足题意的数之和。
再构造f(d, m1, m2)表示任选d个数(0 ～ 9)都成一个新数, 新数各位数字之和除以k余m1, 新数除以k余m2。例如1**形式满足题意的数之和为f(2, (k - 1) % k, (k - 100) % k)。递推方程为f(d, m1, m2) = sum{f(d-1, (m1 - x) % k, (m2 - x * 10^(d-1)) % k) | x = 0, 1, 2...9}。边界条件：if (!d) return (!m1 && !m2)
但是，这样的方法还是会TLE，计算f(d, m1, m2)的部分会有大量重复计算，而打表预处理又由于数据范围太大不能实现。观察题会发现，由于1 <= a <= b < 2^31， 所以a, b各位数字之和一定小于100，所以当k >= 100时答案一定为0，所以可以设置数组f[15][100][100]，避免重复计算。
tag：math, 递推, good
1 /* 2 * Author: plum rain 3 * Created Time: 2013-08-17 10:41 4 * File Name: math-UVa-11361.cpp 5 */ 6 #include<iostream> 7 #include<sstream> 8 #include<fstream> 9 #include<vector> 10 #include<list> 11 #include<deque> 12 #include<queue> 13 #include<stack> 14 #include<map> 15 #include<set> 16 #include<bitset> 17 #include<algorithm> 18 #include<cstdio> 19 #include<cstdlib> 20 #include<cstring> 21 #include<cctype> 22 #include<cmath> 23 #include<ctime> 24 #include<utility> 25 26 using namespace std; 27 28 #define CLR(x) memset(x, 0, sizeof(x)) 29 #define PB push_back 30 #define SZ(v) ((int)(v).size()) 31 #define INF 999999999999 32 #define zero(x) (((x)>0?(x):-(x))<eps) 33 #define out(x) cout<<#x<<":"<<(x)<<endl 34 #define tst(a) cout<<#a<<endl 35 #define CINBEQUICKER std::ios::sync_with_stdio(false) 36 37 typedef vector<int> VI; 38 typedef vector<string> VS; 39 typedef vector<double> VD; 40 typedef long long int64; 41 42 const double eps = 1e-8; 43 const double PI = atan(1.0)*4; 44 const int maxint = 2139062143; 45 46 inline int Mymod( int a , int b ) { int x=a%b;if(x<0) x+=b;return x;} 47 48 int mod; 49 int an[40]; 50 int num[40]; 51 int f[11][100][100]; 52 53 int Mypow(int p, int n) 54 { 55 int sq = 1; 56 while (n > 0){ 57 if (n & 1) 58 sq = sq * p; 59 n /= 2; 60 p = p * p; 61 } 62 return sq; 63 } 64 65 int asklen(int x) 66 { 67 if (!x) return 1; 68 int ret = 0; 69 while (x > 0){ 70 an[ret ++] = x % 10; 71 x /= 10; 72 } 73 return ret; 74 } 75 76 int askf(int d, int m1, int m2) 77 { 78 if (f[d][m1][m2] != -1) 79 return f[d][m1][m2]; 80 81 int ret = 0; 82 if (d == 0){ 83 f[d][m1][m2] = (!m1 && !m2); 84 return (!m1 && !m2); 85 } 86 87 for (int i = 0; i < 10; ++ i){ 88 int mm1 = (m1 - i) % mod; 89 if (mm1 < 0) mm1 += mod; 90 int mm2 = (m2 - i * Mypow(10, d-1)) % mod; 91 if (mm2 < 0) mm2 += mod; 92 ret += askf (d-1, mm1, mm2); 93 } 94 f[d][m1][m2] = ret; 95 return ret; 96 } 97 98 int solve (int x) 99 { 100 int ret = 0; 101 if (x == 0) return 1; 102 if (mod == 1) return x+1; 103 CLR (an), CLR (num); 104 int len = asklen(x); 105 int cnt = 1; 106 cnt = Mypow(10, len-1); 107 for (int i = len-1; i >= 0; -- i){ 108 for (int j = 0; j < an[i]; j ++){ 109 num[i] = j; 110 int m1 = 0, m2 = 0; 111 int tmp = cnt; 112 for (int k = len-1; k >= i; -- k) 113 m1 += num[k], m2 += num[k] * tmp, tmp /= 10; 114 m1 = (mod - m1) % mod, m2 = (mod - m2) % mod; 115 if (m1 < 0) m1 += mod; 116 if (m2 < 0) m2 += mod; 117 ret += askf (i, m1, m2); 118 } 119 num[i] = an[i]; 120 } 121 if (!(x % mod)){ 122 int num_sum = 0; 123 for (int i = 0; i < len; ++ i) 124 num_sum += num[i]; 125 if (!(num_sum % mod)) ++ ret; 126 } 127 return ret; 128 } 129 130 int main() 131 { 132 // freopen("tst.in","r",stdin); 133 // freopen("a.out","w",stdout); 134 // std::ios::sync_with_stdio(false); 135 int T; 136 scanf ("%d", &T); 137 while (T--){ 138 int a, b; 139 scanf ("%d%d%d", &a, &b, &mod); 140 if (mod >= 100) 141 printf ("0\n"); 142 else { 143 memset (f, -1, sizeof (f)); 144 printf ("%d\n", solve (b) - solve (a-1)); 145 } 146 } 147 return 0; 148 }
4、NEERC 2005, LA 3516
题意：给出一个多叉树，每个节点的子节点都有左右之分。从根节点开始，每次尽量王座走，走不通就回溯，把每次遇到的字母记下来，可以得到一个序列。给定一个序列s，问有多少种树与之对应。如ABABABA有如下树对应：
size(s) <= 300。
解法：给定字字符串s。记d(l, r)为s[l]至s[r]之间字符串可以构成多少种数，递推公式为d(l, r) = sum {d(l+1, x-1) * d(x, r) | i+2 <= x <= j, s[i] = s[j] = s[k]}，边界条件if (d[l] != d[r]) return 0; if (l == r) return 1;
同样需要用数组记录，防止重复计算。
tag：math, 递推
1 /* 2 * Author: plum rain 3 * Created Time: 2013-08-18 20:02 4 * File Name: math-LA-3516.cpp 5 */ 6 #include<iostream> 7 #include<sstream> 8 #include<fstream> 9 #include<vector> 10 #include<list> 11 #include<deque> 12 #include<queue> 13 #include<stack> 14 #include<map> 15 #include<set> 16 #include<bitset> 17 #include<algorithm> 18 #include<cstdio> 19 #include<cstdlib> 20 #include<cstring> 21 #include<cctype> 22 #include<cmath> 23 #include<ctime> 24 #include<utility> 25 26 using namespace std; 27 28 #define CLR(x) memset(x, 0, sizeof(x)) 29 #define PB push_back 30 #define SZ(v) ((int)(v).size()) 31 #define INF 999999999999 32 #define zero(x) (((x)>0?(x):-(x))<eps) 33 #define out(x) cout<<#x<<":"<<(x)<<endl 34 #define tst(a) cout<<#a<<endl 35 #define CINBEQUICKER std::ios::sync_with_stdio(false) 36 37 typedef vector<int> VI; 38 typedef vector<string> VS; 39 typedef vector<double> VD; 40 typedef long long int64; 41 42 const double eps = 1e-8; 43 const double PI = atan(1.0)*4; 44 const int maxint = 2139062143; 45 const int mod = 1000000000; 46 47 inline int Mymod( int a , int b ) { int x=a%b;if(x<0) x+=b;return x;} 48 49 string s; 50 int64 d[305][305]; 51 52 int64 f(int l, int r) 53 { 54 if (s[l] != s[r]) return 0; 55 if (l == r) return 1; 56 if (d[l][r] != -1) return d[l][r]; 57 58 int64 ret = 0; 59 for (int i = l+2; i <= r; ++ i) 60 if (s[l] == s[i]) 61 ret = (ret + f(l+1, i) * f(i, r-1)) % mod; 62 d[l][r] = ret; 63 return ret; 64 } 65 66 int main() 67 { 68 // freopen("a.in","r",stdin); 69 // freopen("a.out","w",stdout); 70 // std::ios::sync_with_stdio(false); 71 s.clear(); 72 while (cin >> s){ 73 memset (d, -1, sizeof (d)); 74 for (int i = 0; i < 10; i ++) 75 out (d[i][2]), out (d[2][i]); 76 cout << f(0, SZ (s) - 1) << endl; 77 s.clear(); 78 } 79 return 0; 80 }
5、POJ 2265 Bee Maja
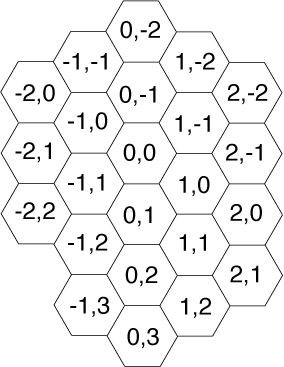
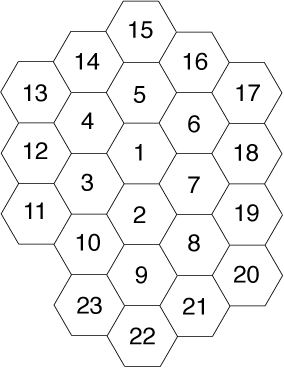
题意：给处下面两张图，输入n，求n在右图中所在的格子，在左图中对应的坐标是多少。
解法：(copy from POJ Discuss..)
首先，记由1到2的方向记为2，1到3的方向记为3……1到7的方向记为7，他们分别是：(0,1),(-1,1),(-1,0),(0,-1),(1,-1),(1,0);这些规律不仅对于1的周围六个方向有效，对于所有的点都是有效的。然后记1所在为圈1，2..7为圈1，8..19为圈2……，所以，很容易可以得到第n圈有蜂窝6n个(n>0)，对于这个等差数列求和，S[1..n]=3n^2+3n，包括第0圈的1，则S[0..n]=3n^2+3n+1。
读入数字x,解方程3n^2+3n+1=x，解出来n=[sqrt(12x-3)-3]/6 如果n为整数，则圈数p=n，否则p=trunc(n)+1，又可以通过公式t:=x-3*sqr(p)+3*p-1;求出t（x是第n圈的第t个）。
可以发现，从上一圈的最后一点，即(p-1,0)走到目的点，首先应在2方向上走1步，再沿(-1,1)走p-1步，其余的5个方向都走p步，此外每走一次，t就要减去相应的值，当t=0时，就可以退出循环，这样就可以很容易得到答案。
tag:math, 找规律
1 /* 2 * Author: Plumrain 3 * Created Time: 2013-10-16 13:01 4 * File Name: math-POJ-2265.cpp 5 */ 6 #include<iostream> 7 #include<cstdio> 8 #include<cmath> 9 10 using namespace std; 11 12 #define zero(x) (((x)>0?(x):-(x))<eps) 13 const double eps = 1e-8; 14 int dir[6][2] = {{0, 1}, {-1, 1}, {-1, 0}, {0, -1}, {1, -1}, {1, 0}}; 15 16 void cha(int x, int& xx, int& yy) 17 { 18 double n = (sqrt(12.0*x - 3) - 3.0) / 6.0; 19 int p = zero(n - ceil(n)) ? (int)n : ceil(n); 20 int t = x - 3 * p * p + 3 * p - 1; 21 xx = p - 1; yy = 0; 22 while (1){ 23 if (!t) return; 24 xx += dir[0][0]; yy += dir[0][1]; 25 -- t; 26 if (!t) return; 27 for (int i = 0; i < p-1; ++ i){ 28 xx += dir[1][0]; yy += dir[1][1]; 29 -- t; 30 if (!t) return; 31 } 32 33 for (int i = 2; i <= 6; ++ i) 34 for (int j = 1; j <= p; ++ j){ 35 xx += dir[i%6][0]; yy += dir[i%6][1]; 36 -- t; 37 if (!t) return; 38 } 39 } 40 } 41 42 int main() 43 { 44 int n; 45 while (scanf ("%d", &n) != EOF){ 46 if (n == 1){ 47 printf ("0 0\n"); 48 continue; 49 } 50 51 int x, y; 52 cha(n, x, y); 53 printf ("%d %d\n", x, y); 54 } 55 return 0; 56 }
6、POJ 1870 Bee Breeding
题意：在下图中，给定两点号码，要从一个点走到另一个点最短的步数是多少。每一步只能走到相邻的六边形。
解法：本来这道题没有建模成六边形，建模之后，加上做过POJ2265(上面那道题)，这道题就很容易了。
tag:math, 建模找规律
1 /* 2 * Author: Plumrain 3 * Created Time: 2013-10-16 14:00 4 * File Name: math-POJ-1870.cpp 5 */ 6 #include <iostream> 7 #include <cstdio> 8 #include <cstring> 9 #include <cmath> 10 #include <algorithm> 11 12 using namespace std; 13 14 #define CLR(x) memset(x, 0, sizeof(x)) 15 #define zero(x) (((x)>0?(x):-(x))<eps) 16 const double eps = 1e-8; 17 const int maxint = 2147483647; 18 19 int dir[6][2] = {{0, 1}, {-1, 1}, {-1, 0}, {0, -1}, {1, -1}, {1, 0}}; 20 int change[6][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, -1}, {-1, 1}}; 21 int x[2], y[2], ans; 22 23 void cha(int x, int& xx, int& yy) 24 { 25 if (x == 1){xx = 0; yy = 0; return;} 26 27 double n = (sqrt(12.0*x - 3) - 3.0) / 6.0; 28 int p = zero(n - ceil(n)) ? (int)n : ceil(n); 29 int t = x - 3 * p * p + 3 * p - 1; 30 xx = p - 1; yy = 0; 31 while (1){ 32 if (!t) return; 33 xx += dir[0][0]; yy += dir[0][1]; 34 -- t; 35 if (!t) return; 36 for (int i = 0; i < p-1; ++ i){ 37 xx += dir[1][0]; yy += dir[1][1]; 38 -- t; 39 if (!t) return; 40 } 41 42 for (int i = 2; i <= 6; ++ i) 43 for (int j = 1; j <= p; ++ j){ 44 xx += dir[i%6][0]; yy += dir[i%6][1]; 45 -- t; 46 if (!t) return; 47 } 48 } 49 } 50 51 int gao() 52 { 53 if (x[0] == x[1] || y[0] == y[1]) 54 return abs(x[0]-x[1] + y[0]-y[1]); 55 56 int tmp1 = x[0] - x[1], tmp2 = y[0] - y[1]; 57 if (tmp1 * tmp2 < 0) 58 return max(abs(tmp1), abs(tmp2)); 59 return abs(tmp1) + abs(tmp2); 60 } 61 62 int main() 63 { 64 int a, b; 65 while (scanf ("%d%d", &a, &b) != EOF && (a || b)){ 66 cha(a, x[0], y[0]); cha(b, x[1], y[1]); 67 68 int ans = gao(); 69 printf ("The distance between cells %d and %d is %d.\n", a, b, ans); 70 } 71 return 0; 72 }
7、POJ 3286 How many 0's?
题意：给定n和m，将n~m之间的所有数写在纸上(包括n和m)，问一共会写多少个0。100会写两个0。
类似UVa 11361，本文第3题。
解法：其实这种问题并不难，但是如果想不清楚，就会怎么都写不对，或者写得非常麻烦把自己都弄晕了。而我目前每次碰到这种题，都没有解出来....
首先设置f(n)表示0~n会写多少个0。只需要求f(m) - f(n-1)即可。
按位考虑，从个位开始。以下一21035为例。由于0也算一种，所以给ans赋初值为1。
个位：个位原先不为0。个位为0以后，该位之前一共有2103种情况(注意之前的部分不能为0,因为不能有前驱0)，该位之后只有一种情况，所以ans += 2103 * 1；
十位：十位原先不为0。十位为0以后，该位之前一共有210种情况，该位之后有10种情况，所以ans += 210 * 10；
百位：注意，百位原先为0。所以有两种情况，一种是百位之前的部分去[1, 20]，之后去[0,99]；另一种情况，百位之前为21，之后取[0,35]；所以ans += 20 * 100 + 36。
......
tag:math, 递推, good
Ps：题解参考http://www.cnblogs.com/zhj5chengfeng/archive/2013/03/24/2977984.html
1 /* 2 * Author: Plumrain 3 * Created Time: 2013-10-16 16:02 4 * File Name: math-POJ-3296.cpp 5 */ 6 #include<iostream> 7 #include<cstdio> 8 #include<cstring> 9 10 using namespace std; 11 12 #define CLR(x) memset(x, 0, sizeof(x)) 13 typedef long long int64; 14 int64 tpow[25]; 15 16 int64 f(int64 x) 17 { 18 if (x < 0) return 0; 19 20 int64 ret = 1, lef = 0; 21 for (int64 i = 1;; ++ i){ 22 if (!x) break; 23 int64 tmp = x % 10; 24 x /= 10; 25 if (tmp) 26 ret += x * tpow[i-1]; 27 else 28 ret += (x-1) * tpow[i-1] + (lef+1); 29 lef += tpow[i-1] * tmp; 30 } 31 return ret; 32 } 33 34 int main() 35 { 36 int64 n, m; 37 tpow[0] = 1; 38 for (int i = 1; i < 25; ++ i) 39 tpow[i] = tpow[i-1] * 10; 40 while (scanf ("%lld%lld", &n, &m) != EOF && m >= 0) 41 printf ("%lld\n", f(m) - f(n-1)); 42 return 0; 43 }
8、POJ 1095 Trees Made to Order
题意：按下图给二叉树排序，输入序号，求二叉树，按下列方式输出所求二叉树。
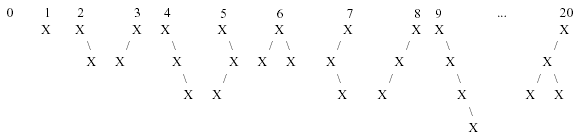
1 - X，2 - X(X)，3 - (X)X，4 - X(X(X))，20 - ((X)X(X))X
解法：首先，发现它是卡特兰数。然后先求树中总共有x个节点，再求左子树右子树各有x1，x2个节点，再求左子树这中形状在有x1个节点的树中排第几个，右子树这种形状在有x2个节点的树中排第几个。
用递归的方法求解并输出。
Ps：参考题解http://blog.csdn.net/lg_mind/article/details/8193841
tag:math, catanlan
1 /* 2 * Author: Plumrain 3 * Created Time: 2013-10-17 11:35 4 * File Name: math-POJ-1095.cpp 5 */ 6 #include<iostream> 7 #include<cstdio> 8 9 using namespace std; 10 11 int catalan[] = {1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190}; 12 13 void gao(int n) 14 { 15 if (!n) return ; 16 17 int x, k; 18 for (int i = 1;; ++ i) 19 if (n > catalan[i]) 20 n -= catalan[i]; 21 else{ 22 k = i; 23 break; 24 } 25 26 if (k == 1){ 27 printf ("X"); 28 return ; 29 } 30 31 for (int i = 0; i < k; ++ i) 32 if (n - catalan[i]*catalan[k-1-i] > 0) 33 n -= catalan[i] * catalan[k-1-i]; 34 else{ 35 x = i; 36 break; 37 } 38 39 int ln = n / catalan[k-1-x] + (n%catalan[k-1-x] != 0); 40 int rn = (n-1) % catalan[k-1-x] + 1; 41 if (x){ 42 int tmp = 0; 43 for (int j = 1; j < x; ++ j) 44 tmp += catalan[j]; 45 printf ("("); 46 gao(ln + tmp); 47 printf (")"); 48 } 49 printf ("X"); 50 if (k - 1 - x){ 51 int tmp = 0; 52 for (int j = 1; j < k - 1 - x; ++ j) 53 tmp += catalan[j]; 54 printf ("("); 55 gao(rn + tmp); 56 printf (")"); 57 } 58 } 59 60 int main() 61 { 62 int n; 63 while (scanf ("%d", &n) != EOF && n){ 64 gao(n); 65 printf ("\n"); 66 } 67 return 0; 68 }
9、HDU 3221 Brute-force Algorithm
题意：给出下面的图片，并给定p，n，a和b，求函数funny会执行多少次。输出执行次数mod P。1 <= n <= 10^9，1 <= P <= 10^6，0 <= a,b <= 10^6。
解法：首先，手算模拟知道，当n = 1,2,3,4,5,6时，答案分别为a, b, ab, ab^2, a^2 * b^3, a^3 * b^5。并且，手算的过程中可以归纳出，当n >= 4，答案就是a^f(n) * b^g(n)，其中f(n)和g(n)分别是两个Fibonacci数列。 但是，还有两个需要解决的问题。
一、n可以到10^9太大了，O(n)的递推是不能被接受的。所以需要用矩阵快速幂优化。
二、Fibonacci数列太大了，会超long long，而且它是作为指数使用，所以不能在计算中途mod P。所以要用到下面的结论：
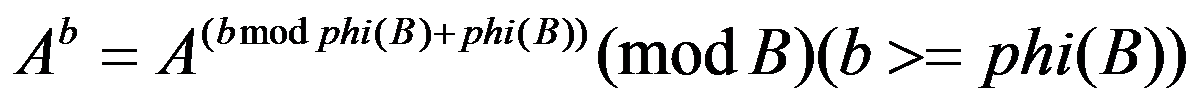（其中A为证数，为矩阵或者浮点数不一定成立）
这样，问题就得到了解决。
tag:math, Fibonacci, 矩阵快速幂, 求幂大法
1 /* 2 * Author: Plumrain 3 * Created Time: 2013-10-28 14:32 4 * File Name: nath-HDU-3221.cpp 5 */ 6 #include<iostream> 7 #include<cstdio> 8 #include<cstring> 9 10 using namespace std; 11 12 #define CLR(x) memset(x, (int64)0, sizeof(x)) 13 const int N = 2000000; 14 typedef long long int64; 15 typedef int64 matrix[10][10]; 16 17 int64 a, b, mod, n; 18 int64 phi[N+5]; 19 bool xxx; 20 matrix at, bt, cnt; 21 22 int64 pow_mod(int64 p, int64 num, int64 mod) 23 { 24 p %= mod; 25 int64 ret = 1; 26 while (num){ 27 if (num & 1) ret = (ret * p) % mod; 28 num >>= 1; 29 p = (p * p) % mod; 30 } 31 return ret; 32 } 33 34 void phi_table(int n) 35 { 36 CLR (phi); 37 phi[1] = 1; 38 for (int i = 2; i <= n; ++ i) 39 if (!phi[i]){ 40 for (int j = i; j <= n; j += i){ 41 if (!phi[j]) phi[j] = j; 42 phi[j] -= phi[j]/i; 43 } 44 } 45 } 46 47 void mtx_init() 48 { 49 at[0][0] = 2; 50 at[1][1] = at[0][1] = at[1][0] = 1; 51 cnt[1][1] = 0; 52 cnt[0][0] = cnt[0][1] = cnt[1][0] = 1; 53 bt[0][0] = 3; 54 bt[0][1] = bt[1][0] = 2; 55 bt[1][1] = 1; 56 } 57 58 void mtx_mul(matrix& A, matrix B) 59 { 60 matrix ret; 61 for (int i = 0; i < 2; ++ i) 62 for (int j = 0; j < 2; ++ j){ 63 ret[i][j] = 0; 64 for (int k = 0; k < 2; ++ k){ 65 ret[i][j] += A[i][k] * B[k][j]; 66 if (xxx || ret[i][j] > N*10){ 67 xxx = 1; 68 ret[i][j] %= mod; 69 } 70 } 71 } 72 73 for (int i = 0; i < 2; ++ i) 74 for (int j = 0; j < 2; ++ j) 75 A[i][j] = ret[i][j]; 76 } 77 78 void mtx_pow(matrix& A, int64 n) 79 { 80 matrix ret; CLR (ret); 81 ret[0][0] = ret[1][1] = 1; 82 while (n){ 83 if (n & 1) mtx_mul(ret, A); 84 n >>= 1; 85 mtx_mul(A, A); 86 } 87 88 for (int i = 0; i < 2; ++ i) 89 for (int j = 0; j < 2; ++ j) 90 A[i][j] = ret[i][j]; 91 } 92 93 int main() 94 { 95 phi_table(N); 96 97 int T, test = 0; 98 scanf ("%d", &T); 99 while (T--){ 100 mtx_init(); 101 xxx = false; 102 103 int64 p; 104 scanf ("%lld%lld%lld%lld", &a, &b, &p, &n); 105 mod = phi[p]; 106 printf ("Case #%d: ", ++test); 107 int64 ans; 108 if (n == 1) 109 ans = a%p; 110 else if (n == 2) 111 ans = b%p; 112 else if (n == 3) 113 ans = (a*b)%p; 114 else{ 115 mtx_pow(cnt, n-4); 116 mtx_mul(at, cnt); 117 mtx_mul(bt, cnt); 118 119 int64 tmp1, tmp2; 120 if (xxx){ 121 tmp1 = pow_mod(a, at[0][1] + mod, p) % p; 122 tmp2 = pow_mod(b, bt[0][1] + mod, p) % p; 123 } 124 else{ 125 tmp1 = pow_mod(a, at[0][1], p) % p; 126 tmp2 = pow_mod(b, bt[0][1], p) % p; 127 } 128 ans = (tmp1 * tmp2) % p; 129 } 130 printf ("%lld\n", ans); 131 } 132 return 0; 133 }
现在的你，在干什么呢？
你是不是还记得，你说你想成为岩哥那样的人。
