POJ 2057 The Lost House

题意：一只蜗牛，它的房子在树上的某个叶子节点上，它要从树的根节点出发，寻找自己的房子。树的任意两个节点的距离为1，房子出现在每个叶子节点上的可能性一样。有的节点上有虫子，如果有虫子，虫子会告诉蜗牛它的房子是不是在这个节点为根的子树上。求蜗牛所走距离的最小期望。

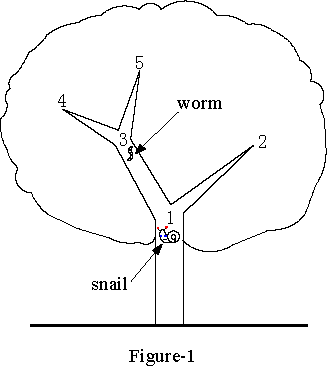
　　　如下图，如果蜗牛制定的策略先到2，再到5再到4，则由于房子地点的不确定，所以可能走的距离为1,4,6，所以期望为11/3。如果制定的策略是先到3,根据虫子的话判断去4和5还是去2，则可能走的距离为2,4,3，所以期望为9/3 = 3。可以证明，最小的期望即为3。

解法：首先，设叶子节点总数为tt，则肯定会有tt种情况，所以只需要求出所有情况下，找到房子所需要走的距离之和即可。

　　　设le[x]表示以x为根的子树上叶子节点的个数；

　　　设su[x]表示在以x为根的子树上，各种情况下找到房子所需走的距离之和；（0为根节点，su[0] / le[0]即为所求）

　　　设fail[x]表示在以x为根的子树上，遍历整个子树没有找到房子又返回x节点所需要走的距离和。

　　　则le[x] += le[v[i]]，v是x的子节点集合；

　　　for (int i = 0; i < v.size(); ++ i) { su[x] += (fail[x] + 1) * le[y] + su[y]；fail[x] += fail[y] + 2;}（这个状态转移方程很精妙，多体会下，最好画个树手算模拟一下）

tag:树形dp, think, good

/*
 * Author:  Plumrain
 * Created Time:  2013-11-20 10:39
 * File Name: (good)DP-POJ-2057.cpp
 */
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

#define CLR(x) memset(x, 0, sizeof(x))
#define PB push_back

int n;
bool w[1005];
vector<int> v[1005];
int le[1005], fail[1005], su[1005];

bool cmp(int x, int y)
{
    return (fail[x]+2)*le[y] < (fail[y]+2)*le[x];
}

void init()
{
    CLR (le); CLR (fail); CLR (su); CLR (w);
    for (int i = 0; i < n; ++ i)
        v[i].clear();

    int t1;
    char s[10];
    for (int i = 0; i < n; ++ i){
        scanf ("%d%s", &t1, s);
        if (s[0] == 'Y') w[i] = 1;
        if (t1 != -1) v[t1-1].PB(i);
    }
}

void dfs(int x)
{
    if (!v[x].size()){
        le[x] = 1;
        su[x] = 0;
        fail[x] = 0;
        return;
    }

    for (int i = 0; i < (int)v[x].size(); ++ i){
        dfs(v[x][i]);
        le[x] += le[v[x][i]];
    }

    sort (v[x].begin(), v[x].end(), cmp);
    for (int i = 0; i < (int)v[x].size(); ++ i){
        int y = v[x][i];
        su[x] += (fail[x]+1)*le[y] + su[y];
        fail[x] += fail[y] + 2; 
    }
    if (w[x]) fail[x] = 0;
}

int main()
{
    while (scanf("%d", &n) != EOF && n){    
        init(); 
        dfs(0);
        printf ("%.4f\n", (double)su[0] / le[0]);
    }
    return 0;
}