SVM算法阅读笔记

硬间隔部分

假定在输入数据集构成的高维空间中，存在一个超平面能够将所有标记的样本分为两类。我们想做的就是求得一个超平面，使得它到最近的数据点的集合距离最大化。即有

 

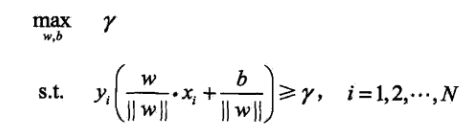
鉴于几何距离直接受w向量的二阶范数影响，问题进行等价归一化后有

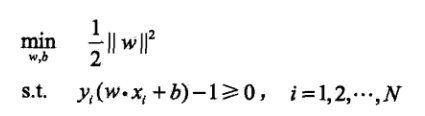
这便是一个原始的凸优化问题。解出了w和b，也就得到了超平面，进而训练好的判断模型也有了。可以证明，只要数据线性可分，那么这样的最优超平面就是存在且唯一的。

直接求w，b不好求，因此我们求解这个凸优化问题的对偶问题。在转化为对偶问题的过程中，需要使用拉格朗日函数及拉格朗日对偶性。为了实现保证对偶问题与原问题有相同解，需要满足KKT条件。详见博客：https://www.cnblogs.com/90zeng/p/Lagrange_duality.html

对偶问题如下：

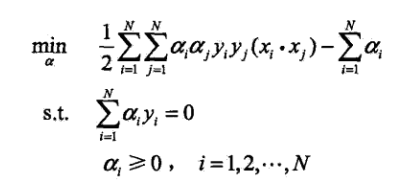
求解出对偶问题，也就得到了参数alpha。可以使用alpha进行如下计算

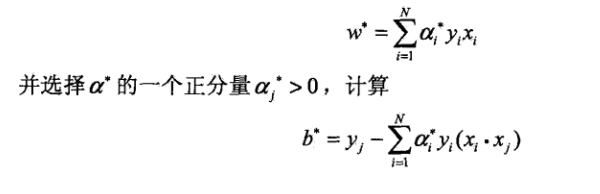
进而解出超平面。

KKT条件保证了对偶问题与原问题的等价性，对于这里的问题，可以写成如下形式

概括来说，KKT条件包含两部分，一个是拉格朗日函数对各个变量的偏导数应该为0，另一个是应满足一些之前的约束条件，如alpha >= 0。

求解对偶问题的个人推导如下：