P1337 [JSOI2004]平衡点 / 吊打XXX
题目描述
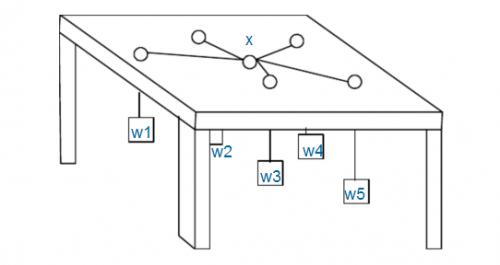
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。
问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入输出格式
输入格式:文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )
输出格式:
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
const int N = 1e6 + 5;
const double eps = 1e-15;
#define RT T *(rand() * 2 - RAND_MAX) //获得randmax~randmax的随机数*T
int n;
struct node
{
int x, y, w;
} p[N];
double bx = 0, by = 0;
double ans = 0;
double D = 0.993;//这个精度控制很重要,调成0.98就容易wa
inline double calc(double x, double y)
{
double res = 0, dx, dy;
For(i, 1, n)
{
dx = x - p[i].x, dy = y - p[i].y;
res += sqrt(dx * dx + dy * dy) * p[i].w;
}
return res;
}
int main()
{
// file("test");
sdf(n);
For(i, 1, n)
sdf(p[i].x),
sdf(p[i].y), sdf(p[i].w);
double best, x0, y0;
double x1, y1, res;
ans = best = 1e18;
// srand(time(NULL));
while (clock() < CLOCKS_PER_SEC * 0.9)//限时反正1秒,那就循环卡到1ms左右呗
{
best = ans, x0 = bx, y0 = by;
for (double T = 100; T > eps; T *= D)
{
x1 = x0 + RT;
y1 = y0 + RT;
res = calc(x1, y1);
if (res < best || exp((best - res) / T) > rand() / (double)RAND_MAX)
{
best = res, x0 = x1, y0 = y1;
if (res < ans)
ans = res, bx = x1, by = y1;
}
}
}
printf("%.3lf %.3lf", bx, by);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号