B. Sleepy Game
http://codeforces.com/problemset/problem/936/B
Petya and Vasya arranged a game. The game runs by the following rules. Players have a directed graph consisting of n vertices and m edges. One of the vertices contains a chip. Initially the chip is located at vertex s. Players take turns moving the chip along some edge of the graph. Petya goes first. Player who can't move the chip loses. If the game lasts for 106 turns the draw is announced.
Vasya was performing big laboratory work in "Spelling and parts of speech" at night before the game, so he fell asleep at the very beginning of the game. Petya decided to take the advantage of this situation and make both Petya's and Vasya's moves.
Your task is to help Petya find out if he can win the game or at least draw a tie.
The first line of input contain two integers n and m — the number of vertices and the number of edges in the graph (2 ≤ n ≤ 105, 0 ≤ m ≤ 2·105).
The next n lines contain the information about edges of the graph. i-th line (1 ≤ i ≤ n) contains nonnegative integer ci — number of vertices such that there is an edge from i to these vertices and cidistinct integers ai, j — indices of these vertices (1 ≤ ai, j ≤ n, ai, j ≠ i).
It is guaranteed that the total sum of ci equals to m.
The next line contains index of vertex s — the initial position of the chip (1 ≤ s ≤ n).
If Petya can win print «Win» in the first line. In the next line print numbers v1, v2, ..., vk (1 ≤ k ≤ 106) — the sequence of vertices Petya should visit for the winning. Vertex v1 should coincide with s. For i = 1... k - 1 there should be an edge from vi to vi + 1 in the graph. There must be no possible move from vertex vk. The sequence should be such that Petya wins the game.
If Petya can't win but can draw a tie, print «Draw» in the only line. Otherwise print «Lose».
5 6
2 2 3
2 4 5
1 4
1 5
0
1
Win
1 2 4 5
3 2
1 3
1 1
0
2
Lose
2 2
1 2
1 1
1
Draw
In the first example the graph is the following:
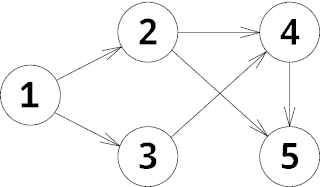
Initially the chip is located at vertex 1. In the first move Petya moves the chip to vertex 2, after that he moves it to vertex 4 for Vasya. After that he moves to vertex 5. Now it is Vasya's turn and there is no possible move, so Petya wins.
In the second example the graph is the following:

Initially the chip is located at vertex 2. The only possible Petya's move is to go to vertex 1. After that he has to go to 3 for Vasya. Now it's Petya's turn but he has no possible move, so Petya loses.
In the third example the graph is the following:
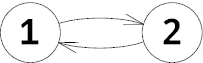
Petya can't win, but he can move along the cycle, so the players will draw a tie.
这题很坑,还是我太弱了,套路太浅
1.这种图论问奇偶数的问题,一定要考虑奇环的存在(走一个奇环可以改变路径的奇偶)(就是这个地方让我一直TLE,mmp)
所以呢,打标记数组改成vis[maxn][2](用上^1),且就是为了防止重复走不必要的一个顶点,此题的dfs回溯不需要清空vis!!!
2.判环的存在这题就直接过程中book掉就好,不过也要去看看tarjan算法(算环的个数)
http://blog.csdn.net/qq_34374664/article/details/77488976
3.判出度为0的学到可以新开一个chu[]存(这样看起来舒服),不用head[u]==0这种,且链式前向星存图注意顶点为0的情况时需要初始化为-1
#include <bits/stdc++.h> using namespace std; typedef long long ll; #define inf 2147483647 const ll INF = 0x3f3f3f3f3f3f3f3fll; #define ri register int template <class T> inline T min(T a, T b, T c) { return min(min(a, b), c); } template <class T> inline T max(T a, T b, T c) { return max(max(a, b), c); } template <class T> inline T min(T a, T b, T c, T d) { return min(min(a, b), min(c, d)); } template <class T> inline T max(T a, T b, T c, T d) { return max(max(a, b), max(c, d)); } #define scanf1(x) scanf("%d", &x) #define scanf2(x, y) scanf("%d%d", &x, &y) #define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z) #define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X) #define pi acos(-1) #define me(x, y) memset(x, y, sizeof(x)); #define For(i, a, b) for (int i = a; i <= b; i++) #define FFor(i, a, b) for (int i = a; i >= b; i--) #define bug printf("***********\n"); #define mp make_pair #define pb push_back const int maxn = 2e5 + 10; // name******************************* struct edge { int to,next; } e[maxn]; int tot=0; int head[maxn]; int n,m,s; int book[maxn]; int vis[maxn][2]; int chu[maxn]; int res[maxn]; int cnt=0; int flag=0; // function****************************** void add(int u,int v) { tot++; e[tot].to=v; e[tot].next=head[u]; head[u]=tot; } void dfs(int u,int mk) { for(int p=head[u]; p; p=e[p].next) { int v=e[p].to; // cout<<"u:"<<u<<" v:"<<v<<" cnt:"<<cnt<<" flag:"<<flag<<" mk:"<<(mk^1)<<endl; if(book[v])flag=1; book[v]=1; if(vis[v][mk^1])continue; vis[v][mk^1]=1; res[++cnt]=v; if(!chu[v]&&!mk) { cout<<"Win"<<endl; For(i,1,cnt) { cout<<res[i]<<" "; } exit(0); } dfs(v,mk^1); book[v]=0; cnt--; } } //*************************************** int main() { ios::sync_with_stdio(0); cin.tie(0); // freopen("test.txt", "r", stdin); // freopen("outout.txt","w",stdout); cin>>n>>m; For(i,1,n) { int t; cin>>t; chu[i]=t; For(j,1,t) { int x; cin>>x; add(i,x); } } cin>>s; book[s]=1; res[++cnt]=s; dfs(s,0); if(flag) cout<<"Draw"; else cout<<"Lose"; return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号