B. Vile Grasshoppers

http://codeforces.com/problemset/problem/937/B

The weather is fine today and hence it's high time to climb the nearby pine and enjoy the landscape.

The pine's trunk includes several branches, located one above another and numbered from 2 to y. Some of them (more precise, from 2 to p) are occupied by tiny vile grasshoppers which you're at war with. These grasshoppers are known for their awesome jumping skills: the grasshopper at branch x can jump to branches .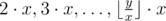

Keeping this in mind, you wisely decided to choose such a branch that none of the grasshoppers could interrupt you. At the same time you wanna settle as high as possible since the view from up there is simply breathtaking.

In other words, your goal is to find the highest branch that cannot be reached by any of the grasshoppers or report that it's impossible.

Input

The only line contains two integers p and y (2 ≤ p ≤ y ≤ 109).

Output

Output the number of the highest suitable branch. If there are none, print -1 instead.

Examples

input

Copy

3 6

output

5

input

Copy

3 4

output

-1

Note

In the first sample case grasshopper from branch 2 reaches branches 2, 4 and 6 while branch 3 is initially settled by another grasshopper. Therefore the answer is 5.

It immediately follows that there are no valid branches in second sample case.

 

 水题

// 去吧！皮卡丘! 把AC带回来！
//      へ　　　　　／|
// 　　/＼7　　　 ∠＿/
// 　 /　│　　 ／　／
// 　│　Z ＿,＜　／　　 /`ヽ
// 　│　　　　　ヽ　　 /　　〉
// 　Y　　　　　`　 /　　/
// 　ｲ●　､　●　　⊂⊃〈　　/
// 　()　 へ　　　　|　＼〈
// 　　>ｰ ､_　 ィ　 │ ／／
// 　 / へ　　 /　ﾉ＜| ＼＼
// 　 ヽ_ﾉ　　(_／　 │／／
// 　　 7　　　　　　　|／
// 　　 ＞―r￣￣`ｰ―＿
//**************************************
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define inf 2147483647
const ll INF = 0x3f3f3f3f3f3f3f3fll;
#define ri register int
template <class T> inline T min(T a, T b, T c) { return min(min(a, b), c); }
template <class T> inline T max(T a, T b, T c) { return max(max(a, b), c); }
template <class T> inline T min(T a, T b, T c, T d) {
  return min(min(a, b), min(c, d));
}
template <class T> inline T max(T a, T b, T c, T d) {
  return max(max(a, b), max(c, d));
}
#define scanf1(x) scanf("%d", &x)
#define scanf2(x, y) scanf("%d%d", &x, &y)
#define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z)
#define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X)
#define pi acos(-1)
#define me(x, y) memset(x, y, sizeof(x));
#define For(i, a, b) for (ll i = a; i <= b; i++)
#define FFor(i, a, b) for (ll i = a; i >= b; i--)
#define bug printf("***********\n");
#define mp make_pair
#define pb push_back
const int maxn = 3e5 + 10;
const int maxx = 1e6 + 10;
// name*******************************
ll p, y;
// function******************************

//***************************************
int main() {
  cin >> p >> y;
  bool flag = true;
  FFor(i, y, p + 1) {
    flag = true;
    for (ll j = 2; j <= p && j * j <= i; j++) {
      if (i % j == 0) {
        flag = false;
        break;
      }
    }
    if (flag) {
      cout << i;
      return 0;
    }
  }
  cout<<-1;

  return 0;
}