P1796 汤姆斯的天堂梦

题目描述

汤姆斯生活在一个等级为0的星球上。那里的环境极其恶劣，每天12小时的工作和成堆的垃圾让人忍无可忍。他向往着等级为N的星球上天堂般的生活。

有一些航班将人从低等级的星球送上高一级的星球，有时需要向驾驶员支付一定金额的费用，有时却又可以得到一定的金钱。

汤姆斯预先知道了从0等级星球去N等级星球所有的航线和需要支付（或者可以得到）的金钱，他想寻找一条价格最低（甚至获得金钱最多）的航线。

输入输出格式

输入格式：

 

第一行一个正整数N(N≤100)，接下来的数据可分为N个段落每段的第一行一个整数Ki(Ki≤100)，表示等级为i的星球有Ki个。

接下来的Ki行中第Tij个依次表示与等级为i，编号为j的星球相连的等级为i-1的星球的编号和此航线需要的费用（正数表示支出，负数表示收益，费用的绝对值不超过1000）。

每行以0结束，每行的航线数≤100。

 

输出格式：

 

输出所需（或所得）费用。正数表示支出，负数表示收益。

 

输入输出样例

输入样例#1： 复制

3
2
1 15 0
1 5 0
3
1 -5 2 10 0
1 3 0
2 40 0
2
1 1 2 5 3 -5 0
2 -19 3 -20 0

输出样例#1： 复制

-1

说明

对于100%的数据N≤100 Ki≤100。

样例解释：

 

 

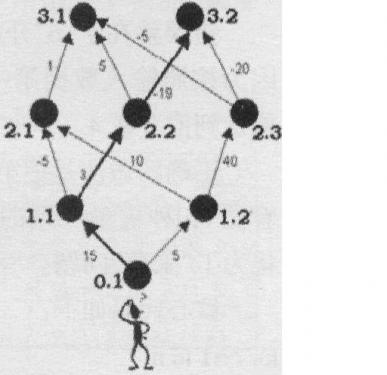
简单dp

用spfa也可以

// 去吧！皮卡丘! 把AC带回来！
//      へ　　　　　／|
// 　　/＼7　　　 ∠＿/
// 　 /　│　　 ／　／
// 　│　Z ＿,＜　／　　 /`ヽ
// 　│　　　　　ヽ　　 /　　〉
// 　Y　　　　　`　 /　　/
// 　ｲ●　､　●　　⊂⊃〈　　/
// 　()　 へ　　　　|　＼〈
// 　　>ｰ ､_　 ィ　 │ ／／
// 　 / へ　　 /　ﾉ＜| ＼＼
// 　 ヽ_ﾉ　　(_／　 │／／
// 　　 7　　　　　　　|／
// 　　 ＞―r￣￣`ｰ―＿
//**************************************
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define inf 2147483647
const ll INF = 0x3f3f3f3f3f3f3f3fll;
#define ri register int
template <class T> inline T min(T a, T b, T c) { return min(min(a, b), c); }
template <class T> inline T max(T a, T b, T c) { return max(max(a, b), c); }
template <class T> inline T min(T a, T b, T c, T d) {
  return min(min(a, b), min(c, d));
}
template <class T> inline T max(T a, T b, T c, T d) {
  return max(max(a, b), max(c, d));
}
#define scanf1(x) scanf("%d", &x)
#define scanf2(x, y) scanf("%d%d", &x, &y)
#define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z)
#define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X)
#define pi acos(-1)
#define me(x, y) memset(x, y, sizeof(x));
#define For(i, a, b) for (int i = a; i <= b; i++)
#define FFor(i, a, b) for (int i = a; i >= b; i--)
#define bug printf("***********\n");
#define mp make_pair
#define pb push_back
const int maxn = 3e5 + 10;
const int maxx = 1e6 + 10;
// name*******************************
int dp[105][105];
int n;
int ans = inf;
// function******************************

//***************************************
int main() {
  // ios::sync_with_stdio(0); cin.tie(0);
  // freopen("test.txt", "r", stdin);
  //  freopen("outout.txt","w",stdout);
  cin >> n;
  int x;
  For(i, 1, n) {
    cin >> x;
    For(j, 1, x) {
      dp[i][j] = inf - 1000;
      int a, b;
      cin >> a;
      while (a) {
        cin >> b;
        dp[i][j] = min(dp[i][j], dp[i - 1][a] + b);
        cin >> a;
      }
    }
  }
  For(i, 1, x) { ans = min(ans, dp[n][i]); }
  cout << ans;
  return 0;
}