P2216 [HAOI2007]理想的正方形
题目描述
有一个a*b的整数组成的矩阵,现请你从中找出一个n*n的正方形区域,使得该区域所有数中的最大值和最小值的差最小。
输入输出格式
输入格式:
第一行为3个整数,分别表示a,b,n的值
第二行至第a+1行每行为b个非负整数,表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。
输出格式:
仅一个整数,为a*b矩阵中所有“n*n正方形区域中的最大整数和最小整数的差值”的最小值。
输入输出样例
说明
问题规模
(1)矩阵中的所有数都不超过1,000,000,000
(2)20%的数据2<=a,b<=100,n<=a,n<=b,n<=10
(3)100%的数据2<=a,b<=1000,n<=a,n<=b,n<=100
线性ST表的变式:
dp[i][j][k]:代表以坐标(i,j)左上角,边长为2^k的正方形的最大差值
(类比线性ST表,它更新的方法是:一个区间取出两个相同长度(2^n)部分)
所以这里用来更新的方法应该是:一个正方形区间取出四个相同面积部分
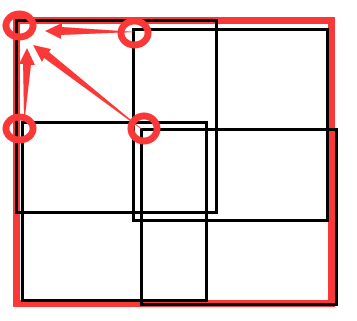
dp[i][j][k]=opt(dp[i][j][k-1],dp[i][j+(1<<(k-1))][k-1],dp[i+(1<<(k-1))][j][k-1],dp[i+(1<<(k-1))][j+(1<<(k-1))][k-1]);
1.三维
正常纯矩阵ST表

#include<bits/stdc++.h> using namespace std; #define maxn 1005 typedef long long ll; #define inf 2147483647 #define ri register int #define getchar() (Ss==Tt&&(Tt=(Ss=BB)+fread(BB,1,1<<15,stdin),Ss==Tt)?EOF:*Ss++) char BB[1 << 18], *Ss = BB, *Tt = BB; inline int read() { int x=0; int ch=getchar(),f=1; while (!isdigit(ch)&&(ch!='-')&&(ch!=EOF)) ch=getchar(); if (ch=='-') { f=-1; ch=getchar(); } while (isdigit(ch)) { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); } return x*f; } int a,b; int n; int S[maxn][maxn][11]; int T[maxn][maxn][11]; int l,K; int query(int x1,int y1,int x2,int y2) { int t=1<<l; int MIN=min(min(S[x1][y1][l],S[x2-t+1][y1][l]), min(S[x1][y2-t+1][l],S[x2-t+1][y2-t+1][l]) ); int MAX=max(max(T[x1][y1][l],T[x1][y2-t+1][l]), max(T[x2-t+1][y2-t+1][l],T[x2-t+1][y1][l]) ); return MAX-MIN; } int main() { memset(S,0x3f,sizeof(S)); // freopen("test.txt","r",stdin); a=read(),b=read(),n=read(); for(int i=1; i<=a; i++) for(int j=1; j<=b; j++) S[i][j][0]=T[i][j][0]=read(); K=log2(min(a,b)); l=log2(n); for(int k=1; k<=K; k++) { int t=1<<(k-1); for(int i=1; i<=a-t; i++) for(int j=1; j<=b-t; j++) { S[i][j][k]=min(min(S[i][j][k-1],S[i][j+t][k-1]), min(S[i+t][j][k-1],S[i+t][j+t][k-1]) ); T[i][j][k]=max(max(T[i][j][k-1],T[i][j+t][k-1]), max(T[i+t][j][k-1],T[i+t][j+t][k-1]) ); } } int ans=inf; for(int i=1; i<=a-n+1; i++) for(int j=1; j<=b-n+1; j++) { // cout<<query(i,j,i+n-1,j+n-1)<<endl; ans=min(ans,query(i,j,i+n-1,j+n-1)); } cout<<ans; return 0; }
2. 二维优化
仔细发现显然可以压成二维,省去k长度那一维,不影响结果
在三维的基础上,令dp[i][j]=min(dp[i][j][0~k]) k为log2(n)

#include<bits/stdc++.h> using namespace std; #define maxn 1005 typedef long long ll; #define inf 2147483647 #define ri register int #define getchar() (Ss==Tt&&(Tt=(Ss=BB)+fread(BB,1,1<<15,stdin),Ss==Tt)?EOF:*Ss++) char BB[1 << 18], *Ss = BB, *Tt = BB; inline int read() { int x=0; int ch=getchar(),f=1; while (!isdigit(ch)&&(ch!='-')&&(ch!=EOF)) ch=getchar(); if (ch=='-') { f=-1; ch=getchar(); } while (isdigit(ch)) { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); } return x*f; } int a,b; int n; int S[maxn][maxn]; int T[maxn][maxn]; int l,K; int query(int x1,int y1,int x2,int y2) { int t=1<<l; int MIN=min(min(S[x1][y1],S[x2-t+1][y1]), min(S[x1][y2-t+1],S[x2-t+1][y2-t+1]) ); int MAX=max(max(T[x1][y1],T[x1][y2-t+1]), max(T[x2-t+1][y2-t+1],T[x2-t+1][y1]) ); return MAX-MIN; } int main() { memset(S,0x3f,sizeof(S)); // freopen("test.txt","r",stdin); a=read(),b=read(),n=read(); for(int i=1; i<=a; i++) for(int j=1; j<=b; j++) S[i][j]=T[i][j]=read(); l=log2(n); for(int k=1; k<=l; k++) { int t=1<<(k-1); for(int i=1; i<=a-t; i++) for(int j=1; j<=b-t; j++) { S[i][j]=min(min(S[i][j],S[i][j+t]), min(S[i+t][j],S[i+t][j+t]) ); T[i][j]=max(max(T[i][j],T[i][j+t]), max(T[i+t][j],T[i+t][j+t]) ); } } int ans=inf; for(int i=1; i<=a-n+1; i++) for(int j=1; j<=b-n+1; j++) { // cout<<query(i,j,i+n-1,j+n-1)<<endl; ans=min(ans,query(i,j,i+n-1,j+n-1)); } cout<<ans; return 0; }
3.ST表+单调队列
先创线性的ST表得到每行的opt值,然后选择指定行数,再单调队列处理
mi[i][j][k]:代表第i行,从第j列向右长度为2^k范围中最小数
如果是线性的话qmi这里应该是由一个head,一个tail代替
但是这里是矩阵,还要考虑行的存在
qmi[i][1]:用来存真正最小数
qmi[i][0]:用来存横坐标,控制范围防止越界

#include<bits/stdc++.h> using namespace std; #define maxn 1005 typedef long long ll; #define inf 9999999999 #define re register inline int read() { int x=0; int ch=getchar(),f=1; while (!isdigit(ch)&&(ch!='-')&&(ch!=EOF)) ch=getchar(); if (ch=='-') { f=-1; ch=getchar(); } while (isdigit(ch)) { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); } return x*f; } //读优 int ma[maxn][maxn][11],mi[maxn][maxn][11]; int qma[maxn][2],qmi[maxn][2]; int n,m,t; int ans=inf; //查询第k行的第x列到第y列的最大值 int queryma(int k,int x1,int x2) { int l=log2(x2-x1+1);//刚好覆盖或大于x2-x1一半的2的幂指数 return max(ma[k][x1][l],ma[k][x2-(1<<l)+1][l]); } int querymi(int k,int x1,int x2) { int l=log2(x2-x1+1); return min(mi[k][x1][l],mi[k][x2-(1<<l)+1][l]); } int main() { // freopen("test.txt","r",stdin); n=read(),m=read(),t=read(); int l=log2(max(n,m)); fill(&mi[0][0][0],&mi[maxn-1][maxn-1][10],inf); for(int i=1; i<=n; i++) for(int j=1; j<=m; j++) ma[i][j][0]=mi[i][j][0]=read(); for(int i=1; i<=n; i++) for(int k=1; k<=l; k++) { int x=1<<(k-1); for(int j=1; j<=m-x; j++) { ma[i][j][k]=max(ma[i][j][k-1],ma[i][j+x][k-1]); mi[i][j][k]=min(mi[i][j][k-1],mi[i][j+x][k-1]); } } //遍历列(找起点) for(int i=1; i<=m; i++) { if(i+t-1>m)break; int h1=1,h2=1; int t1=0,t2=0; //单调队列:每次寻找最具潜力的数,然后删掉那些没用的数 for(int j=1; j<=n; j++) { int x=queryma(j,i,i+t-1);//横向比较,询问第j行,取出(i~i+t-1)中最大数 while(x>=qma[t1][1]&&h1<=t1)t1--;//这里是纵向比较 qma[++t1][1]=x; qma[t1][0]=j;//同时记录行 x=querymi(j,i,i+t-1); while(x<=qmi[t2][1]&&h2<=t2)t2--; qmi[++t2][1]=x; qmi[t2][0]=j; //为了满足这个正方形,横坐标小于(j-t)都不属于这个范围,所以h++,跳到单调队列的下一个点 if(j>=t) { while(j-t>=qma[h1][0])h1++; while(j-t>=qmi[h2][0])h2++; ans=min(ans,qma[h1][1]-qmi[h2][1]); } } } cout<<ans; return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号