[学习笔记] 树链剖分

$emmmm$我终于可以整理树剖啦!好歹学会了……不过为什么树剖代码也这么长啊QAQ~~（很难背的~~

# $0x00$、树剖的意义

我们知道如果要维护一个数列，对它进行区间修改、区间求和、区间查询，那么我们可以用线段树；

那么如果要维护一个数列，对它进行区间修改、插入删除、区间反转、区间循环移动之类的诡异操作，我们可以用splay。

那么我们考虑将其拓展到树上：如果这棵树只有一条链，我们自然是可以在这条链上建树的。所以我们考虑将整棵树解剖成几条链。随机剖分的复杂度可以达到期望$log$，但我们也可以把它优化成稳定的$log$——轻重链剖分。

# $0x01$、树剖的前置技能——轻重链及其性质

对于这棵Tree，我们定义以当前节点为根的子树大小（节点数目）为$sub$，那么：

重儿子：相对于一个非叶子节点$p$而言，他的所有的儿子中$sub$最大的那个节点，称其为重儿子。

轻儿子：初重儿子之外的所有儿子都为$p$的轻儿子。

重边：连接重儿子与当前节点的边。轻边：以此类推。

重链：由一堆重儿子和一堆重边组成的链。轻链：就是轻边

轻重链剖分之后，我们会发现有这么几个性质：

重链上的点集合$U$，与树上的点集合$V$满足关系$U = V$（证明：显然）
重链段数 $ = $轻边数 $ + \ \ 1$，即，轻重链剖分之后，所有不同的重链由轻边所连接。
从叶子节点向上遍历时，每经过一条轻边，子树大小至少翻一倍，即对于一条轻边$(u,v)$，$sub(u) \times 2 < sub(v)$

我们可以尝试去证明以上两个显然的性质。

证明一：重链之间由轻链相连接

我们对于随机的一条轻边$E \ \ = \ \ u,v$，它一定会有父亲~~（废话）~~，那么他的父亲一定是重链的一部分。那么不妨设其父亲为$u$，则节点$v$必然也会有以自己为开始的一条重链，所以对于一条任意的轻边，总是连接着两条重链。

证明二：对于一条轻边$E \ \ = \ \ (u,v)$，$sub(u) \times 2 < sub(v)$

不妨设$u$为父亲，$v$为儿子，那么由于$E$是一条轻边，所以$u$必然另有一个重儿子$w$，那么之所以$w$能够成为重儿子，那么一定会有$sub(w) > sub(v)$，所以对于$u$而言，$sub(u) >= sub(w) + sub(v)$，即可得到$sub(u) \times 2 < sub(v)$。

~~这真是我今年来经历过的最简单的证明~~

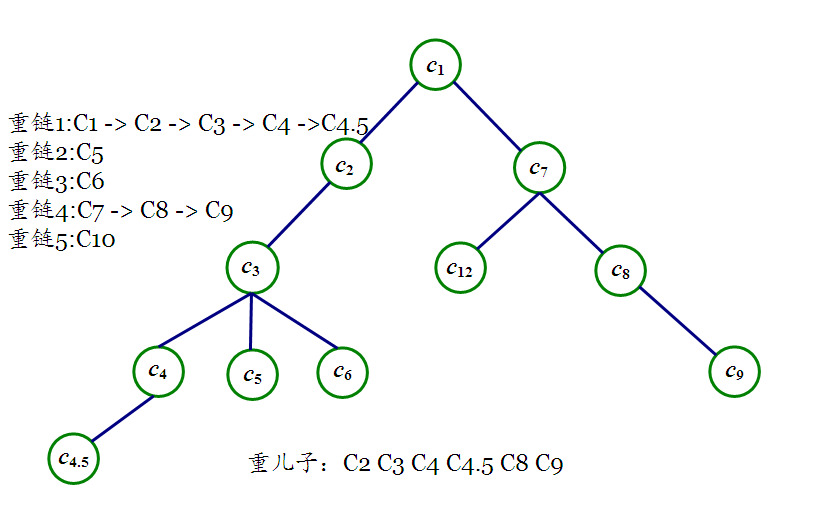
嗯，不要在意为什么编号会出现4.5，因为我太弱了所以打错了$QAQ$，如果你明白了轻重链这部分的话你就会知道我是怎么打错的了$ORZ$

# $0x02$、树剖的算法流程（这里以维护节点权值之和为例子）

我们先执行两遍$dfs$，一遍用来确定轻重儿子$+$建树$+$确定父子关系$+$确定子树大小，一遍用来找$dfs$序($Obviously$，同一条重链上的节点编号必须保证连续)。

第一遍：

void dfs1(int rt, int f, int deep){
    fa[rt] = f ,dep[rt] = deep ,sub[rt] = 1 ;
    int hson = -1 ;//用于比较的变量
    for(int k = head[rt]; k ; k = e[k].next){
        if (to(k) == f) continue ;
        dfs1(to(k), rt, deep + 1) ;
        sub[rt] += sub[to(k)] ;//回溯时++
        if (sub[to(k)] > hson ) hs[rt] = to(k), hson = sub[to(k)] ;//确定重儿子
    }
}

第二遍

void dfs2(int now, int tp){
    nid[now] = ++ tot ,top[now] = tp ,aft[tot] = base[now] ;//确定dfs序
    if (!hs[now]) return ;
    dfs2(hs[now], tp) ;//先从重儿子向下找（先走重链）
    for(int k = head[now]; k ; k = e[k].next){
        if (to(k) == fa[now] || to(k) == hs[now]) continue ;
        dfs2(to(k), to(k)) ;//如果有分叉，那么top需要重新定义
    }
}

然后我们对$dfs$序建一棵线段树或者什么树的，对其进行最朴素的线段树构造。

il void p_d(int rt, int l, int r){//Segment Tree
    int mid = (l + r) >> 1 ;
    tag[ls(rt)] += tag[rt], tag[rs(rt)] += tag[rt] ;
    s[ls(rt)] += tag[rt] * (mid - l + 1), s[rs(rt)] += tag[rt] * (r - mid) ;
    s[ls(rt)] %= p, s[rs(rt)] %= p ;
    tag[rt] = 0 ;
} 
void build(int rt, int l, int r){
    if(l == r){
        s[rt] = aft[l];
        if(s[rt] > p) s[rt] %= p ;
        return ;
    }
    int mid = (l + r) >> 1 ;
    build(ls(rt), l, mid) ;
    build(rs(rt), mid + 1, r) ;
    s[rt] = (s[ls(rt)] + s[rs(rt)]) % p ;
}

void update(int l, int r, int ul, int ur, int rt, int k){
    if(ul <= l && ur >= r){
        s[rt] = s[rt]  + k * (r - l + 1);  
        tag[rt] += k ;        
        return ;
    }
    int mid = (l + r) >> 1 ;
    if(tag[rt])p_d(rt, l, r) ;
    if(ul <= mid) update(l, mid, ul, ur, ls(rt), k) ;
    if(ur > mid) update(mid + 1, r, ul, ur, rs(rt), k) ;
    s[rt] = (s[ls(rt)] + s[rs(rt)]) % p ;
}
int query(int l, int r, int ql, int qqr, int rt){
    int rs = 0 ;
    if(ql <= l && qqr >= r){
        rs = (rs + s[rt]) % p ;
        return rs ;
    }
    int mid = (l + r) >> 1 ;
    p_d(rt, l, r) ;
    if(ql <= mid) rs += query(l, mid, ql, qqr, ls(rt)) ;
    if(qqr > mid) rs += query(mid + 1, r, ql, qqr, rs(rt)) ;
    return rs ;
}

之后我们在确定树上结点的时候，譬如编号区间$[l,r]$，如果他们在一条重链上就直接查询；否则我们考虑，让他们~~在一起~~在同一条重链上，呐，因为我们维护的是每个重链上的讯息，所以必须这么做。那么我们如何让他们~~在一起~~在同一条重链上呢？因为从普遍意义上讲，我们只需要让其中一个点不断向上跳，直到~~在一起~~在同一条重链上为止，而在这个地方比较显然的是，我们只能让深度大的向上跳，否则就GG了$qwq$

呐~既然在同一条重链上了，编号连续，我们就可以考虑直接线段树查找或修改即可，$over$.

void updv(int u, int v, int k){
	k %= p ;
    while(top[u] != top[v]){
        if(dep[top[u]] < dep[top[v]]) swap(u, v) ;
        update(1, N, nid[top[u]], nid[u], 1, k)  ;
        u = fa[top[u]] ;
    }
    if(dep[u] > dep[v]) swap(u, v) ;
    update(1, N, nid[u], nid[v], 1, k) ;
}
int qv(int u, int v){
    int ans = 0;
    while(top[u] != top[v]){
        if(dep[top[u]] < dep[top[v]]) swap(u, v) ;
        ans = ((ans % p) + query(1, N, nid[top[u]], nid[u], 1)) % p;
        u = fa[top[u]] ;
    }
    if(dep[u] > dep[v]) swap(u, v) ;
    ans = ans + query(1, N, nid[u], nid[v], 1) ;    
    return ans % p;
}

嗯……分析时间复杂度的话呢，应该是是$O(max(n,mlogn))$的，因为首先你的两遍$dfs$就已经$O(n)$了，如果是$m$次查询、修改，那也至多是期望$O(logn)$的复杂度（除非故意卡你）。嗯……差不多就是这样了。

# $0x03$、举个栗子

譬如这道模板题：link

$\color{red}{\mathcal{Description}}$

你有一棵树，你要对这棵树进行这样的操作：

操作$1$：格式： $1 \ \ x \ \ y \ \ z$ 表示将树从$x$到$y$结点最短路径上所有节点的值都加上$z$

操作$2$：格式： $2 \ \ x \ \ y$ 表示求树从$x$到$y$结点最短路径上所有节点的值之和

操作$3$：格式： $3 \ \ x \ \ z$ 表示将以$x$为根节点的子树内所有节点值都加上$z$

操作$4$：格式： $4 \ \ x$ 表示求以$x$为根节点的子树内所有节点值之和

$\color{red}{\mathcal{Solution}}$

其实就是一个很裸的树剖~~（废话）~~，那我们对于子树的操作也很简单，子树的节点连续，查询即可。

void upds(int f, int k){
    update(1, N, nid[f], nid[f] + sub[f] - 1, 1, k) ;
}
int qs(int f){
    return query(1, N, nid[f], nid[f] + sub[f] - 1, 1) ; 
}

那么贴一下代码：

// luogu-judger-enable-o2
#include<cstdio>
#include<iostream>
#define il inline 
#define MAXN 300001
#define to(k) e[k].t
#define ls(x) x << 1
#define rs(x) x << 1 | 1
#define int long long  

using namespace std;
char c ;
int N, M, R, p, i, j, base[MAXN], aft[MAXN], nid[MAXN], a, b, g, cnt, head[MAXN], mark, tot, k;
int fa[MAXN], sub[MAXN], dep[MAXN], hs[MAXN], top[MAXN], s[MAXN << 2], tag[MAXN << 2] ; 
struct edge{
    int t, next ;
}e[MAXN];
il int qr(){//Preparation
    k = 0, c = getchar();
    while(!isdigit(c)) c = getchar() ;
    while(isdigit(c)){
        k = (k << 3) + (k << 1) + c - 48, c = getchar() ; 
    }
    return k ;
}
il void add(int f, int t){
    e[++ cnt].t = t ;
    e[cnt].next = head[f] ;
    head[f] = cnt ; 
}
il void p_d(int rt, int l, int r){//Segment Tree
    int mid = (l + r) >> 1 ;
    tag[ls(rt)] += tag[rt], tag[rs(rt)] += tag[rt] ;
    s[ls(rt)] += tag[rt] * (mid - l + 1), s[rs(rt)] += tag[rt] * (r - mid) ;
    s[ls(rt)] %= p, s[rs(rt)] %= p ;
    tag[rt] = 0 ;
} 
void build(int rt, int l, int r){
    if(l == r){
        s[rt] = aft[l];
        if(s[rt] > p) s[rt] %= p ;
        return ;
    }
    int mid = (l + r) >> 1 ;
    build(ls(rt), l, mid) ;
    build(rs(rt), mid + 1, r) ;
    s[rt] = (s[ls(rt)] + s[rs(rt)]) % p ;
}

void update(int l, int r, int ul, int ur, int rt, int k){
    if(ul <= l && ur >= r){
        s[rt] = s[rt]  + k * (r - l + 1);  
        tag[rt] += k ;        
        return ;
    }
    int mid = (l + r) >> 1 ;
    if(tag[rt])p_d(rt, l, r) ;
    if(ul <= mid) update(l, mid, ul, ur, ls(rt), k) ;
    if(ur > mid) update(mid + 1, r, ul, ur, rs(rt), k) ;
    s[rt] = (s[ls(rt)] + s[rs(rt)]) % p ;
}
int query(int l, int r, int ql, int qqr, int rt){
    int rs = 0 ;
    if(ql <= l && qqr >= r){
        rs = (rs + s[rt]) % p ;
        return rs ;
    }
    int mid = (l + r) >> 1 ;
    p_d(rt, l, r) ;
    if(ql <= mid) rs += query(l, mid, ql, qqr, ls(rt)) ;
    if(qqr > mid) rs += query(mid + 1, r, ql, qqr, rs(rt)) ;
    return rs ;
}
void dfs1(int rt, int f, int deep){//Cut this Tree
    fa[rt] = f ,dep[rt] = deep ,sub[rt] = 1 ;
    int hson = -1 ;
    for(int k = head[rt]; k ; k = e[k].next){
        if (to(k) == f) continue ;
        dfs1(to(k), rt, deep + 1) ;
        sub[rt] += sub[to(k)] ;
        if (sub[to(k)] > hson ) hs[rt] = to(k), hson = sub[to(k)] ;
    }
}
void dfs2(int now, int tp){
    nid[now] = ++ tot ,top[now] = tp ,aft[tot] = base[now] ;
    if (!hs[now]) return ;
    dfs2(hs[now], tp) ;
    for(int k = head[now]; k ; k = e[k].next){
        if (to(k) == fa[now] || to(k) == hs[now]) continue ;
        dfs2(to(k), to(k)) ;
    }
}
void updv(int u, int v, int k){
	k %= p ;
    while(top[u] != top[v]){
        if(dep[top[u]] < dep[top[v]]) swap(u, v) ;
        update(1, N, nid[top[u]], nid[u], 1, k)  ;
        u = fa[top[u]] ;
    }
    if(dep[u] > dep[v]) swap(u, v) ;
    update(1, N, nid[u], nid[v], 1, k) ;
}
int qv(int u, int v){
    int ans = 0;
    while(top[u] != top[v]){
        if(dep[top[u]] < dep[top[v]]) swap(u, v) ;
        ans = ((ans % p) + query(1, N, nid[top[u]], nid[u], 1)) % p;
        u = fa[top[u]] ;
    }
    if(dep[u] > dep[v]) swap(u, v) ;
    ans = ans + query(1, N, nid[u], nid[v], 1) ;    
    return ans % p;
}

void upds(int f, int k){
    update(1, N, nid[f], nid[f] + sub[f] - 1, 1, k) ;
}
int qs(int f){
    return query(1, N, nid[f], nid[f] + sub[f] - 1, 1) ; 
}
int main(){
    cin >> N >> M >> R >> p;
    for(i = 1; i <= N; i ++) base[i] = qr();
    for(i = 1; i < N ; i ++) a = qr(), b = qr(), add(a, b), add(b, a) ;
    dfs1(R, 0, 1) ;
    dfs2(R, R) ;
    build(1, 1, N) ;
    for(i = 1; i <= M; i ++){
        mark = qr();
        if (mark == 1) a = qr(), b = qr(), g = qr(), updv(a, b, g) ;
        else if (mark == 2) a = qr(), b = qr(), printf("%lld\n", qv(a, b) % p) ;
        else if (mark == 3) a = qr(), b = qr(), upds(a, b) ;
        else a = qr(), printf("%lld\n", qs(a) % p) ;
    }
    return 0 ;
}

嗯，撒花花$qwq$

posted @ 2018-06-18 04:14 皎月半洒花阅读(371) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

$\mathcal{\color{skyblue}{\_Orchid}\color{violet}{any}}$

大踏步地向明天走去吧

[学习笔记] 树链剖分

# \(0x00\)、树剖的意义

# \(0x01\)、树剖的前置技能——轻重链及其性质

# \(0x02\)、树剖的算法流程（这里以维护节点权值之和为例子）

# \(0x03\)、举个栗子

公告