VK Cup 2016 - Round 1 (Div. 2 Edition) C. Bear and Forgotten Tree 3

A tree is a connected undirected graph consisting of n vertices and n - 1 edges. Vertices are numbered 1 through n.

Limak is a little polar bear and Radewoosh is his evil enemy. Limak once had a tree but Radewoosh stolen it. Bear is very sad now because he doesn't remember much about the tree — he can tell you only three values n, d and h:

The tree had exactly n vertices.
The tree had diameter d. In other words, d was the biggest distance between two vertices.
Limak also remembers that he once rooted the tree in vertex 1 and after that its height was h. In other words, h was the biggest distance between vertex 1 and some other vertex.

The distance between two vertices of the tree is the number of edges on the simple path between them.

Help Limak to restore his tree. Check whether there exists a tree satisfying the given conditions. Find any such tree and print its edges in any order. It's also possible that Limak made a mistake and there is no suitable tree – in this case print "-1".

Input

The first line contains three integers n, d and h (2 ≤ n ≤ 100 000, 1 ≤ h ≤ d ≤ n - 1) — the number of vertices, diameter, and height after rooting in vertex 1, respectively.

Output

If there is no tree matching what Limak remembers, print the only line with "-1" (without the quotes).

Otherwise, describe any tree matching Limak's description. Print n - 1 lines, each with two space-separated integers – indices of vertices connected by an edge. If there are many valid trees, print any of them. You can print edges in any order.

Examples
input
5 3 2
output
1 2
1 3
3 4
3 5
input
8 5 2
output
-1
input
8 4 2
output
4 8
5 7
2 3
8 1
2 1
5 6
1 5

Note

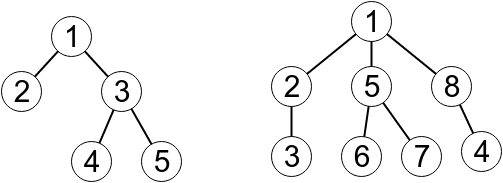
Below you can see trees printed to the output in the first sample and the third sample.

$\text{[math]}$

构造。

每次先以1为根构造深度为h的一支树杈1-2-3...h，如果h==d那么就在2下面接上1个节点如果h！=d 那么就在1下面接上d-h个节点。

注意h==d的时候。2 1 1是有解的。

/* ***********************************************
Author        :guanjun
Created Time  :2016/3/29 9:49:51
File Name     :cfvk1c.cpp
************************************************ */
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <iomanip>
#include <list>
#include <deque>
#include <stack>
#define ull unsigned long long
#define ll long long
#define mod 90001
#define INF 0x3f3f3f3f
#define maxn 100010
#define cle(a) memset(a,0,sizeof(a))
const ull inf = 1LL << 61;
const double eps=1e-5;
using namespace std;
priority_queue<int,vector<int>,greater<int> >pq;
struct Node{
    int x,y;
};
struct cmp{
    bool operator()(Node a,Node b){
        if(a.x==b.x) return a.y> b.y;
        return a.x>b.x;
    }
};

bool cmp(int a,int b){
    return a>b;
}
vector<int>v[maxn];
int main()
{
    #ifndef ONLINE_JUDGE
    //freopen("in.txt","r",stdin);
    #endif
    //freopen("out.txt","w",stdout);
    int n,d,h;
    while(cin>>n>>d>>h){
        if(d>h*2){
            puts("-1");continue;
        }
        int num=1;
        int vec,w;
        if(d==h){
            if(h==1&&n>2){
                cout<<-1<<endl;continue;
            }
            vec=2,w=d-h+1;
        }
        else vec=1,w=d-h;
        for(int i=1;i<=h;i++){
            v[num].push_back(num+1);
            num++;
        }
        for(int i=1;i<=d-h;i++){
            if(i==1)v[vec].push_back(num+1);
            else v[num].push_back(num+1);
            num++;
            //puts("-1");
        }
        //cout<<"num "<<num<<endl;
        int mark=0;
        while(1){
            if(num==n)break;
            for(int i=1;i<=w;i++){
                if(i==1)v[vec].push_back(num+1);
                else v[num].push_back(num+1);
                num++;
                if(num==n){
                    mark=1;break;
                }
            }
            if(mark)break;
        }
        for(int i=1;i<=n;i++){
            for(int j=0;j<v[i].size();j++){
                cout<<i<<" "<<v[i][j]<<endl;
            }
        }
    }
    return 0;
}