Codeforces Round #338 (Div. 2)

A. Bulbs

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Vasya wants to turn on Christmas lights consisting of m bulbs. Initially, all bulbs are turned off. There are n buttons, each of them is connected to some set of bulbs. Vasya can press any of these buttons. When the button is pressed, it turns on all the bulbs it's connected to. Can Vasya light up all the bulbs?

If Vasya presses the button such that some bulbs connected to it are already turned on, they do not change their state, i.e. remain turned on.

Input

The first line of the input contains integers n and m (1 ≤ n, m ≤ 100) — the number of buttons and the number of bulbs respectively.

Each of the next n lines contains xi (0 ≤ xi ≤ m) — the number of bulbs that are turned on by the i-th button, and then xi numbers yij(1 ≤ yij ≤ m) — the numbers of these bulbs.

Output

If it's possible to turn on all m bulbs print "YES", otherwise print "NO".

Sample test(s)

input

3 4
2 1 4
3 1 3 1
1 2

output

YES

input

3 3
1 1
1 2
1 1

output

NO

Note

In the first sample you can press each button once and turn on all the bulbs. In the 2 sample it is impossible to turn on the 3-rd lamp.

 

/* ***********************************************
Author        :guanjun
Created Time  :2016/2/2 10:21:03
File Name     :cf338a.cpp
************************************************ */
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <iomanip>
#include <list>
#include <deque>
#include <stack>
#define ull unsigned long long
#define ll long long
#define mod 90001
#define INF 0x3f3f3f3f
#define maxn 10000+10
#define cle(a) memset(a,0,sizeof(a))
const ull inf = 1LL << 61;
const double eps=1e-5;
using namespace std;

bool cmp(int a,int b){
    return a>b;
}
int a[maxn];
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif
    //freopen("out.txt","w",stdout);
    int n,m,x;
    while(cin>>n>>m){
        cle(a);
        for(int i=1;i<=n;i++){
            
            cin>>x;
            int y;
            for(int j=1;j<=x;j++){
                cin>>y;
                a[y]=1;
            }
        }
        int mark=0;
        for(int i=1;i<=m;i++){
            if(a[i]==0){
                mark=1;
                break;
            }
        }
        if(mark)puts("NO");
        else puts("YES");
    }
    return 0;
}

B. Longtail Hedgehog

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

This Christmas Santa gave Masha a magic picture and a pencil. The picture consists of n points connected by m segments (they might cross in any way, that doesn't matter). No two segments connect the same pair of points, and no segment connects the point to itself. Masha wants to color some segments in order paint a hedgehog. In Mashas mind every hedgehog consists of a tail and some spines. She wants to paint the tail that satisfies the following conditions:

1. Only segments already presented on the picture can be painted;
2. The tail should be continuous, i.e. consists of some sequence of points, such that every two neighbouring points are connected by a colored segment;
3. The numbers of points from the beginning of the tail to the end should strictly increase.

Masha defines the length of the tail as the number of points in it. Also, she wants to paint some spines. To do so, Masha will paint all the segments, such that one of their ends is the endpoint of the tail. Masha defines the beauty of a hedgehog as the length of the tail multiplied by the number of spines. Masha wants to color the most beautiful hedgehog. Help her calculate what result she may hope to get.

Note that according to Masha's definition of a hedgehog, one segment may simultaneously serve as a spine and a part of the tail (she is a little girl after all). Take a look at the picture for further clarifications.

Input

First line of the input contains two integers n and m(2 ≤ n ≤ 100 000, 1 ≤ m ≤ 200 000) — the number of points and the number segments on the picture respectively.

Then follow m lines, each containing two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — the numbers of points connected by corresponding segment. It's guaranteed that no two segments connect the same pair of points.

Output

Print the maximum possible value of the hedgehog's beauty.

Sample test(s)

input

8 6
4 5
3 5
2 5
1 2
2 8
6 7

output

9

input

4 6
1 2
1 3
1 4
2 3
2 4
3 4

output

12

Note

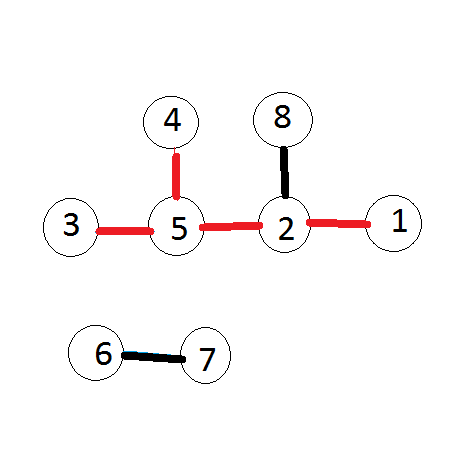
The picture below corresponds to the first sample. Segments that form the hedgehog are painted red. The tail consists of a sequence of points with numbers 1, 2 and 5. The following segments are spines: (2, 5), (3, 5) and (4, 5). Therefore, the beauty of the hedgehog is equal to 3·3 = 9.

题目描述有点长 看了半天。

题意是：给你一些点和边。没有重边。找出编码连续上升的序列的点的数量*这个序列尾部那个端点的度数 的最大值。

正着见图 写dfs超时了（当时没考虑清楚 是否使用记忆法搜索）。

正确解法 反着建图。比如样例2    4->1  4->2  4->3  3->1 3->2  2->1

类似于dp

f[u]=max(f[u],f[v]);//f[u]代表以u结尾能得到的最大的尾巴长度（就是点的数量）

/* ***********************************************
Author        :guanjun
Created Time  :2016/2/2 11:04:18
File Name     :cf338b.cpp
************************************************ */
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <iomanip>
#include <list>
#include <deque>
#include <stack>
#define ull unsigned long long
#define ll long long
#define mod 90001
#define INF 0x3f3f3f3f
#define maxn 1000000+10
#define cle(a) memset(a,0,sizeof(a))
const ull inf = 1LL << 61;
const double eps=1e-5;
using namespace std;
struct node{
    int v;
    int next;
}edge[maxn*2];
int l;
ll de[maxn];
int pre[maxn];
ll f[maxn];
void add(int u,int v){
    edge[l].v=v;
    edge[l].next=pre[u];
    pre[u]=l++;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif
    //freopen("out.txt","w",stdout);
    int n,m;
    while(cin>>n>>m){
        int x,y;
        cle(de);//度数
        l=0;
        memset(pre,-1,sizeof pre);
        for(int i=1;i<=m;i++){
            scanf("%d%d",&x,&y);
            if(x<y)swap(x,y);
            add(x,y);
            de[x]++;
            de[y]++;
        }
        ll ans=-1;
        for(int i=1;i<=n;i++){
            for(int j=pre[i];j+1;j=edge[j].next){
                int v=edge[j].v;
                f[i]=max(f[i],f[v]);
            }
            f[i]++;
        }
        for(int i=1;i<=n;i++){
            ans=max(ans,f[i]*de[i]);
        }
        printf("%I64d\n",ans);
    }
    return 0;
}