2023.6 水题记录

1. CF1190B Tokitsukaze, CSL and Stone Game

博弈论. 首先把一开始就会输的情况判掉, 然后容易发现石子最终一定会被取成 \(0,1,\cdots,k\) 的形式.

计算需要取走的石子数, 判断奇偶性即可.

2. [AGC002E] Candy Piles

还是博弈论. 偷一张官方题解的图:

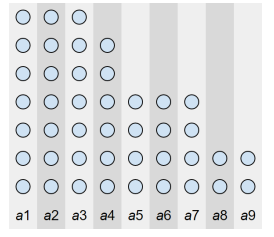
按石子数量排序后容易发现操作就是取最左边一行或最下面一列, 就相当于将棋子向右向上从原点移到边界直到不能动.

找规律容易发现每一条左下/右上的斜线的胜负是相同的, 结合角上的必败, 能简单求出胜负情况.

3. P3750 [六省联考 2017] 分手是祝愿

经典题.

一个显而易见的观察是关灯的方案只能是从大到小关, 并且这是最优的. (每个灯都不能用其他灯开关的组合替代, 根据因数性质这是显然的)

于是我们设 \(f_i\) 为从还有 \(i\) 个需要按的键到还有 \(i-1\) 个需要按的键的期望步数.

有 \(f_i=\dfrac{i}{n}\times 1+\dfrac{n-i}{n}(f_{i+1}+f_i+1)\), 因为按错了还要按回来.

变形得 \(f_i\) 与 \(f_{i+1}\) 的递推式, 初始化 \(f_{n+1}=0\).

具体操作时, 先手动模拟一遍得到需要按键的次数 \(c\).

若 \(c\leqslant k\) 直接按就行; 否则答案应为 \(k+f_{k+1}+\cdots+f_{c}\).

4. P7895 『JROI-3』删树

你需要这个式子: \(s=\sum\limits_{i=2}^n \text{dis}(1,i)(2-d_i)\)

其中 \(s\) 为边权和, \(\text{dis}\) 表示距离, \(d_i\) 表示度数.

式子的证明本身并不难, 容斥即可.

5. P4345 [SHOI2015]超能粒子炮·改

题解区写的可以说是一个看不懂, 于是又写了一个.

运算均在模 \(p(=2333)\) 意义下进行.

\(\begin{aligned}f(n,k)&=\sum\limits_{i=0}^k\dbinom{n}{i}\\&=\sum\limits_{i=0}^k\dbinom{n\bmod p}{i\bmod p}\dbinom{\lfloor n/p\rfloor}{\lfloor i/p\rfloor}\end{aligned}\)

枚举 \(i\bmod p\):

\(\begin{aligned}f(n,k)&=\sum\limits_{r=0}^{p-1}\dbinom{n\bmod p}{r}\left(\sum\limits_{i=0}^k[i\bmod p=r]\dbinom{\lfloor n/p\rfloor}{\lfloor i/p\rfloor}\right)\\&=\sum\limits_{r=0}^{p-1}\dbinom{n\bmod p}{r}\left(\sum\limits_{t=0}^{\lfloor(k-r)/p\rfloor}\dbinom{\lfloor n/p\rfloor}{t}\right)\\&=\sum\limits_{r=0}^{p-1}\dbinom{n\bmod p}{r}f(\lfloor n/p\rfloor,\lfloor(k-r)/p\rfloor)\end{aligned}\)

其中 \(k\geqslant p\). \(k<p\) 时直接有 \(f(n,k)=\sum\limits_{i=0}^k\dbinom{n\bmod p}{i\bmod p}\dbinom{\lfloor n/p\rfloor}{\lfloor i/p\rfloor}=\sum\limits_{i=0}^k\dbinom{n\bmod p}{i}=f(n\bmod p,k)\).

然后发现后面 \(\lfloor(k-r)/p\rfloor\) 的取值很少.

因为 \(r\in[0,p-1]\), 容易发现只可能有 \(\lfloor k/p\rfloor-1,\lfloor k/p\rfloor\) 两种取值.

具体地, 若 \(r\in[0,k\bmod p]\), \(\lfloor(k-r)/p\rfloor=\lfloor k/p\rfloor\);

若 \(r\in [k\bmod p+1,p-1]\), \(\lfloor(k-r)/p\rfloor=\lfloor k/p\rfloor-1\).

注意第二个式子的 \(r\) 可能是不存在的.

为了避免种种问题, 我们可以先都按 \(\lfloor k/p\rfloor-1\) 算, 然后再把实际为 \(\lfloor k/p\rfloor\) 的部分再加上.

\(\begin{aligned}f(n,k)&=\sum\limits_{r=0}^{p-1}\dbinom{n\bmod p}{r}f(\lfloor n/p\rfloor,\lfloor(k-r)/p\rfloor)\\&=\sum\limits_{r=0}^{p-1}\dbinom{n\bmod p}{r}f(\lfloor n/p\rfloor,\lfloor k/p\rfloor-1)+\sum\limits_{r=0}^{k\bmod p}\dbinom{n\bmod p}{r}\dbinom{\lfloor n/p\rfloor}{\lfloor k/p\rfloor}\\&=f(n\bmod p,p-1)f(\lfloor n/p\rfloor,\lfloor k/p\rfloor-1)+\dbinom{\lfloor n/p\rfloor}{\lfloor k/p\rfloor}f(n\bmod p,k\bmod p)\end{aligned}\)

递归计算即可. 注意各种边界.

6. P8207 [THUPC2022 初赛] 最小公倍树

数论优化建图题.
大致的精神就是, 连一些边,使得:

• 边数比较少.
• 包含了所有的可能在最小公倍树上的边.
• 连完之后是连通图.

然后跑 Kruskal 就完事了.

因为要让 \(\text{lcm}\) 尽可能小, 我们可以枚举 \(\gcd\), 这样相同 \(\gcd\) 的时候让两个数的乘积尽可能小即可.

具体地, 我们这样建图:
枚举 \(d\), 考虑位于 \([l,r]\) 中的 \(d\) 的倍数. 我们直接将所有的数都向最小的数 \(l_d\) 连边.
这样在不考虑别的因数的情况下, 这样连边就是最优的.

7. P2260 [清华集训2012]模积和

整除分块板子. 但是式子很难看.
(实际上是把远古时期写挂的程序给调过去了)

8. P5110 块速递推

直接算递推式, 发现二次剩余存在, 然后上光速幂板子就完事了.

9. P5367 【模板】康托展开

简单数数题. 容易发现, 若当前为从左向右第 \(i\) 位, 有 \(k\) 个数字未被使用且小于当前数, 则排名多加上 \(k(n-i)!\) 即可.
\(k\) 可以用树状数组简单维护.

10. UVA11525 Permutation

逆康托展开. 这道题过于善良直接给了每次有几个数字未被使用且小于当前数, 还是直接线段树二分/树状数组上倍增 就能做到 \(O(n\log n)\). 不过简单地暴力二分 \(O(n\log^2n)\) 也可以接受.

11. P9374 「DROI」Round 2 单图

被 MLE 手把手教了属于是.

容易发现单图只能由一车只有出度的点, 没有出度的点和二元环组成.
二元环是简单的, 只需要枚举点数 \(2k\), 则种类数即为 \((2k-1)!!\).
对于其他情况, 枚举只有出度的点数 \(x\), 则没有出度的点即有 \(n-2k-x\) 个, 此时情况数为 \((2^{n-2k-x}-1)^x\).
综合上述情况, 答案即为

\[\sum\limits_{k=0}^{\lfloor n/2\rfloor}\dbinom{n}{2k}(2k-1)!!\sum\limits_{x=0}^{n-2k}\dbinom{n-2k}{x}(2^{n-2k-x}-1)^x \]

预处理组合数即可.

12. P4451 [国家集训队]整数的lqp拆分

生成函数简单应用. 下设斐波那契数列为 \(f_n\), 其生成函数为 \(F(x)=\dfrac{x}{1-x-x^2}\).
设 \(g_n\) 为答案的单项值, \(G(x)\) 为其生成函数.
容易发现,

\[\begin{cases}g_n=1,&n=0\\g_n=\sum\limits_{i=0}^ng_if_{n-i},&n>0\end{cases} \]

根据卷积形式容易得到生成函数满足 \(G(x)=1+F(x)G(x)\), 解出 \(G(x)\) 还原成单项即可.

13. [ARC158D] Equation

怪题. 注意两边齐次且恰好差一次, 我们可以随机一组 \((x,y,z)\), 算出左边是右边的 \(t\) 倍.
则若存在逆元, \((x/t,y/t,z/t)\) 即为解.

14. CF1809D Binary String Sorting

发现最多交换一次, 做完了.

15. CF615D Multipliers

没脑子题, 答案平方后显然为 \(n^{\varphi(n)}\).

16. CF1027E Inverse Coloring

• 发现一行一列就能确定全部.
• 最大的同色子矩形的面积就是第一行和第一列的最长同色段的长度之积.

所以对着最长同色段 dp 以下就完事了.

17. CF476D Dreamoon and Sets

只需考虑两两互质的情况, 最后再乘上 \(k\) 就完事了.
发现偶数太多了, 考虑通过一些方法让一个偶数配三个奇数, 且两两互质.
发现 \((6x+1,6x+2,6x+3,6x+5)\) 刚好满足. 于是做完了.

18. P4643 [国家集训队] 阿狸和桃子的游戏

边权平分给点权.

19. P8347 「Wdoi-6」另一侧的月

小清新博弈论. 直接上结论: 若存在度数为偶数的点则先手必胜, 否则后手必胜.
证明是容易的. 因为只要存在度数为偶数的点, 总有一种方案能使保留的部分的所有点的度数为奇数, 而若所有的点为奇数则只能成为含有度数为偶数的点的情况. 这就对应了必胜态和必败态之间的转化.

20. P3492 [POI2009] TAB-Arrays

对着行和列随便哈希以下就完事了.

21. P8865 [NOIP2022] 种花

枚举 \(\mathtt{C}\) 的左下角和 \(\mathtt{F}\) 的三度点处.