一些简单的图论模型和建图技巧
内容受作者水平所限难度不高. 需要进一步学习的推荐 这一篇.
1. 常见模型
先有模型, 而后有建图技巧.
二分图和网络流那一套建图不是这篇文章讨论的内容.
看上去全是最短路相关的建图(
本来想写 2-SAT 的, 但是那部分内容已经包含在 SCC 和 BCC 那一篇文章里了.
1. 差分约束系统
这个东西应该是耳熟能详的了.
我们知道最短路里有这个不等式: \(d_y\leqslant d_x+w_{x,y}\)
那么有 \(d_y-d_x\leqslant w_{x,y}\). 然后就能用来做题了.
一般有下面几种变形：
- \(x_i-x_j\leqslant c_k\): 直接连边 \(j\xrightarrow{c_k}i\).
- \(x_i-x_j\geqslant c_k\): 即 \(x_j-x_i\leqslant -c_k\), 连边 \(i\xrightarrow{-c_k}j\).
- \(x_i-x_j=c_k\): 前面两种情况合起来.
- \(\dfrac{x_i}{x_j}\gtreqless c_k\): 取对数就成为了上面的三种情况.
(咕咕咕)
luoguP7515 [省选联考 2021 A 卷] 矩阵游戏
2. 同余最短路
同余最短路还是比较抽象的.
直接看题.
有一个显而易见的性质: 如果 \(a\) 能被表出, 那么 \(a+x\) 也能被表出.
因此我们只需要对 \(a\in[0,x-1]\) 求出满足 \(n\equiv a\pmod x\) 且能用 \(y,z\) 表出的最小的 \(n\).
记上面的式子中 \(n=f(a), a\in[0,x-1]\), 则有转移:
我们发现不好确定转移顺序.
但是我们发现这两个式子和最短路不等式 \(d_y=\min\{d_x+w_{x,y}\}\) 非常相似, 并且 \(a\) 的范围一定, 所以我们就可以连边跑最短路了!
具体地, 我们连边 \(a\xrightarrow{y}(a+y)\bmod x, a\xrightarrow{z}(a+z)\bmod x\), 并且发现 \(f(0)=0\). 则以 \(0\) 为源点跑最短路, 得出的 \(d_u\) 就对应了 \(f(u)\).
最后枚举每种余数统计答案即可.
代码可以参考下面的题.
同上, 记得将模数选得尽量小.
//只放 main 函数
signed main()
{
n=read();l=read();r=read();
int ncnt=0;
for(int i=1;i<=n;i++)
{
int x=read();
if(x!=0)a[++ncnt]=x;
}
if(ncnt==0)
{
printf("0\n");
return 0;
}
n=ncnt;
sort(a+1,a+n+1);
for(int u=0;u<a[1];u++)
for(int i=2;i<=n;i++)
addedge(u,(u+a[i])%a[1],a[i]);
dijkstra();
for(int i=0;i<a[1];i++)
{
if(dis[i]<=r)ans+=(r-dis[i])/a[1]+1;
if(dis[i]<=l-1)ans-=(l-1-dis[i])/a[1]+1;
}
printf("%lld\n",ans);
return 0;
}
注意到长度为 \(l_i\) 的木棍有无限根等价于长度在 \([L_i-M,L_i]\) 间的木棍都有无限根, 然后就和上面的基本一样了.
需要注意的是无解情况的判断. 使用数学知识我们知道无解等价于存在长度为 \(1\) 的木棍或者所有木棍长度的 \(\gcd\) 大于 \(1\).
AT3621 [ARC084B] Small Multiple
仿照上面的思路, 设 \(f(a)\) 为最小的 \(S(ka+s)\).
考虑每次在最后加一位 \(S\) 的变化, 有 \(f((10a+b)\bmod k)=\min\{f(a)+b\}\), 然后就可以做了.
但事实上我们有一个更简单的做法. 我们发现所有的数都可以通过一系列乘 \(10\) 加 \(1\) 来得到, 而这两步操作对 \(S\) 的影响就是 \(0\) 和 \(1\). (不必考虑进位, 因为进位一定不优)
for(int i=1;i<K;i++)
{
addedge(i,(i+1)%K,1);
addedge(i,i*10%K,0);
}
dijkstra();//init: dis[1]=1
printf("%d\n",dis[0]);
3. 分层图最短路
容易发现我们要求的就是 \(1\) 到每个点的最短奇数路径和最短偶数路径.
容易发现走一条边就会使奇数和偶数互换, 所以我们直接把图建成两层, 原图上的边对应两层图之间的边即可.
典题.
直接建 \(k+1\) 层图, 层内和原图一样, 从上一层向下一层连边权为 \(0\) 的边表示免费坐一次飞机.
最后跑一遍从第 \(1\) 层的城市 \(s\) 开始的最短路就完事了.
4. 对偶图最短路
luoguP4001 [ICPC-Beijing 2006] 狼抓兔子
众所周知, 平面图最小割=对偶图最短路.
画个图感性理解一下, 会发现 \(S'\) 到 \(T'\) 的最短路和 \(S\) 和 \(T\) 间的最小割的联系.
注意 \(S',T'\) 的连边和 \(S,T\) 位置的关系.
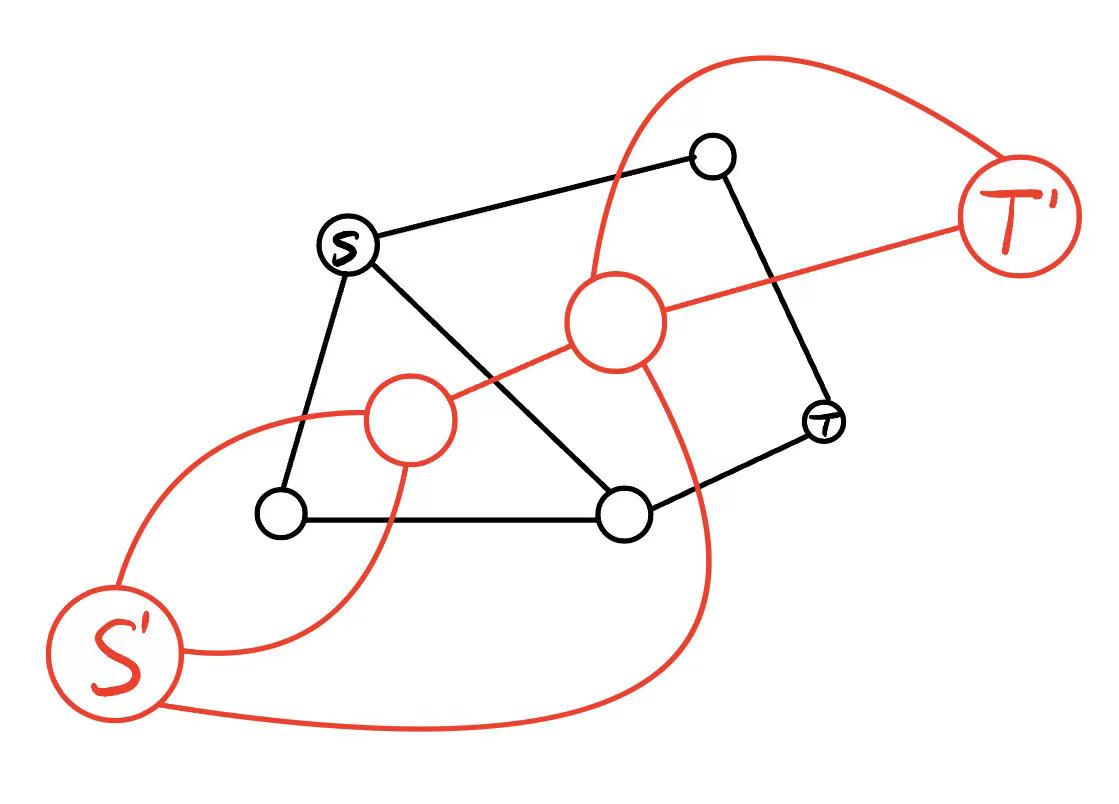
然后就做完了. 不过对偶图有点难建.
为什么 CSP-S 会考这种东西啊.
先考虑 \(k=2\) 且两个点颜色不同的情况. 容易发现此时两种颜色只会有一条分界线, 于是就变成了上面那道题.
再考虑 \(k=3\). 我们发现可以把相邻两个相同颜色结点合并, 就变成了 \(k=2\) 的情况.
\(k\) 更大的情况就会有两种颜色的点交替出现的情况了. 怎么办呢?
首先我们发现可以直接暴力跑出每对不同颜色的点间的最小割.
看上去我们可以寻找一种黑点和白点的匹配方案, 然后将匹配方案对应的最小割全部加起来 (先不要考虑重叠的情况).
然后可以注意到有一个很强的性质: 匹配方案不会有交叉, 换句话说, 如果将匹配的一组看成一堆括号, 那么最终的方案一定是合法的括号序列.
这是因为如果匹配方案有交叉, 那么它们的对应的最小割也会有交叉, 我们直接从交叉点重新分成不交叉的两组, 结果一定不劣.
转化成括号序列就可以区间 dp 了.
设 \(f(l,r)\) 为对区间 \([l,r]\) 匹配得到的最小值, \(cut(i,j)\) 为 \(i,j\) 间的最小割.
容易发现有状态转移方程 \(f(l,r)=\min\{f(l+1,r-1)+cut(l,r),f(l,x)+f(x+1,r)\}\).
等等好像还没有考虑有重叠的情况?
事实上重叠的情况一定不优, 因为如果我们删掉重叠的部分分成左右两部分, 方案就会更优.
(以上性质皆为感性理解, 证明我是不会的)
(口胡完了, 代码就咕咕咕了)
2. 建图技巧
1. 反向建边
luoguP3916 图的遍历
简明题意: 给定一张有向图, 求出从每个点出发能到达的编号最大的点.
看上去并不好做. 考虑缩点将问题反过来, 从大到小枚举到达的点, 反向建边进行遍历即可. 并且如果当前遍历到的结点在原图上能到达编号更大的结点,那就不需要在遍历它了, 这保证了复杂度.
代码略.
2. 虚点连边
显然道路边权为 \(D\), 航线边权为 \(T_i-D\), 然后最长路.
但是你发现源点可以是 \(n\) 个点中的任意一个, 终点也可以是 \(n\) 个点中的任意一个.
于是考虑建立超级源点和超级汇点, 从超级源点向 \(n\) 个点连边权为 \(D\) 的边, \(n\) 个点向超级汇点连边权为 \(0\) 的边, 于是只用跑一遍最长路就行了.
代码略.
3. 线段树优化建图
这题有两种需要处理的情况, 单点向区间连边和区间向单点连边, 但是区别不大.
看到区间, 考虑线段树, 这样用 \(O(\log n)\) 的点就能代表一段区间, 每次只需要连 \(O(\log n)\) 条边.
然后你发现单点向区间和区间向单点重复了. 不过我们只需要开两棵线段树, 每次操作从一棵线段树的单点连向另一棵线段树的区间即可.
最后的效果: (\(4\) 向 \([1,2]\) 连边, \([3,4]\) 向 \(2\) 连边)
代码可以看下一题.
区间向区间连边.
首先考虑一种比较简单的优化方法, 就是新建一个点 \(S\), 让所有的边都经过 \(S\), 朴素实现需要 \(O(nm)\) 条边.
大概就是这样:
但是你发现新建完这个点之后就又变成了区间向单点连边和单点向区间连边!
直接用上一题的建图方式优化即可.
简单应用. 一眼差分约束, 然后发现有区间连边, 直接线段树优化建图, 做完了!
代码不给了(
4. 一些奇怪的建图技巧
比较明显的 2-SAT, 但是对于每个部分恰有一个关键点的判断, 我们直接暴力连边是 \(n^2\) 级别的.
但是这道题的数据很水, 这样做能 92 分
也可以尝试用线段树优化建图, 但是我们甚至有更快的方法: 前/后缀优化建图.
前后缀优化适用于单点/前后缀区间向前后缀区间连边. 具体地, 直接新建 \(2n\) 个点表示前缀后缀, 然后像线段树优化建图一样的思路, 将 \(pre_i\) 连向 \(pre_{i-1}\) 和 \(i\) 即可.
这样对于每个点只需要向前后缀分别连一条边就行了!
你告诉我这是套路题?
首先我们会有这样的想法: 对每个边新建一个点, 把无向边拆成有向边, 枚举形如 \(a\rarr b\rarr c\) 的所有路径, 连接 \((a,b)\rarr(c,d)\), 权值为两条边边权的最大值. 从 \(1\) 出发和到达 \(n\) 的边分别与源点和汇点相连, 跑一遍最短路就行了.
画出图来大概是这样:
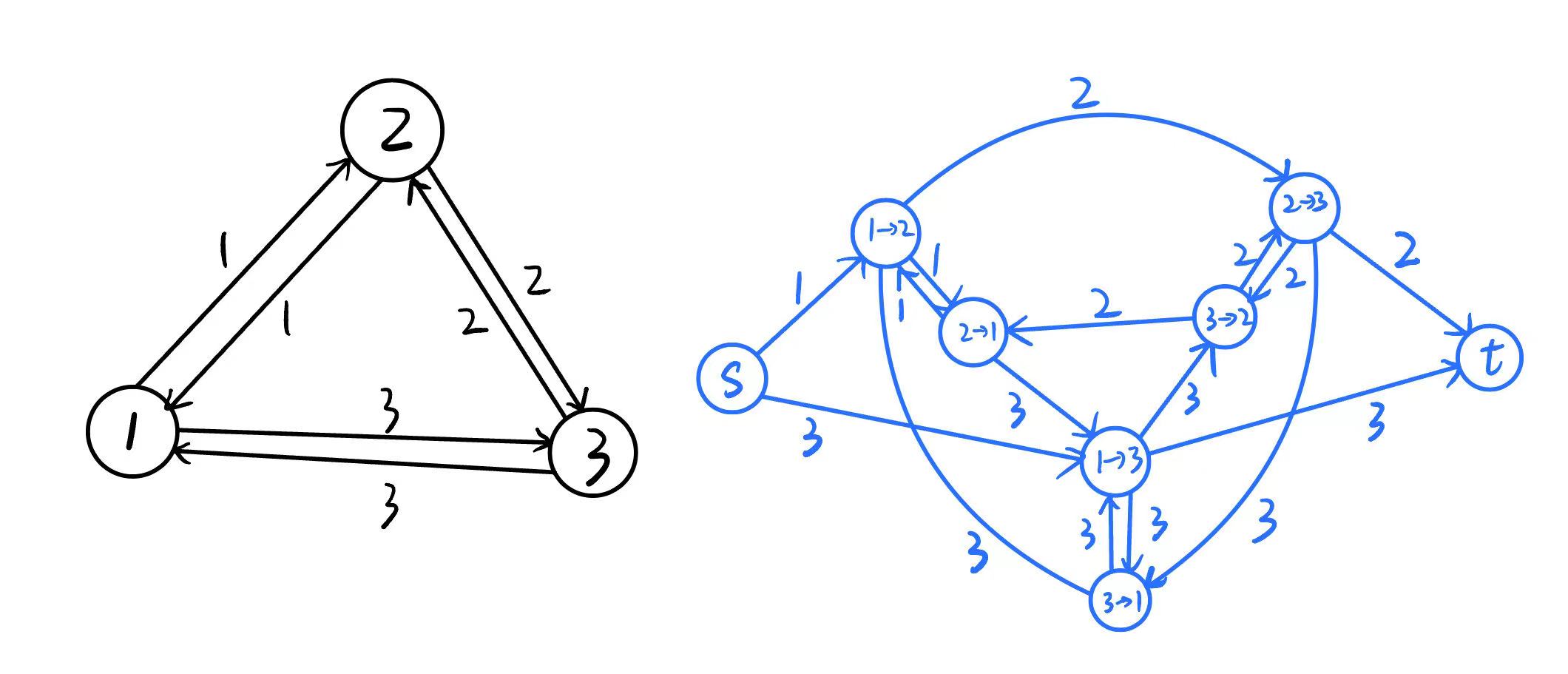
边数 \(O(m^2)\), 不可接受.
为什么会连这么多边呢? 发现问题在于, 对于原图上一个点 \(u\), 和与它相连的边 \((u,v_i),(v_i,u) (i\in[1,k])\), 虽然说只有 \(k\) 个不同权值, 但是我们却连出了 \(O(k^2)\) 条边, 造成了浪费.
方法是, 考虑差分. 对与 \(u\) 相连的边的边权排序, 只在相邻边权间连边. 从权值小的边连向权值大的边的权值为两权值的差, 从权值大的边连向权值小的边权值为 \(0\), 效果就等同于取 \(\max\).
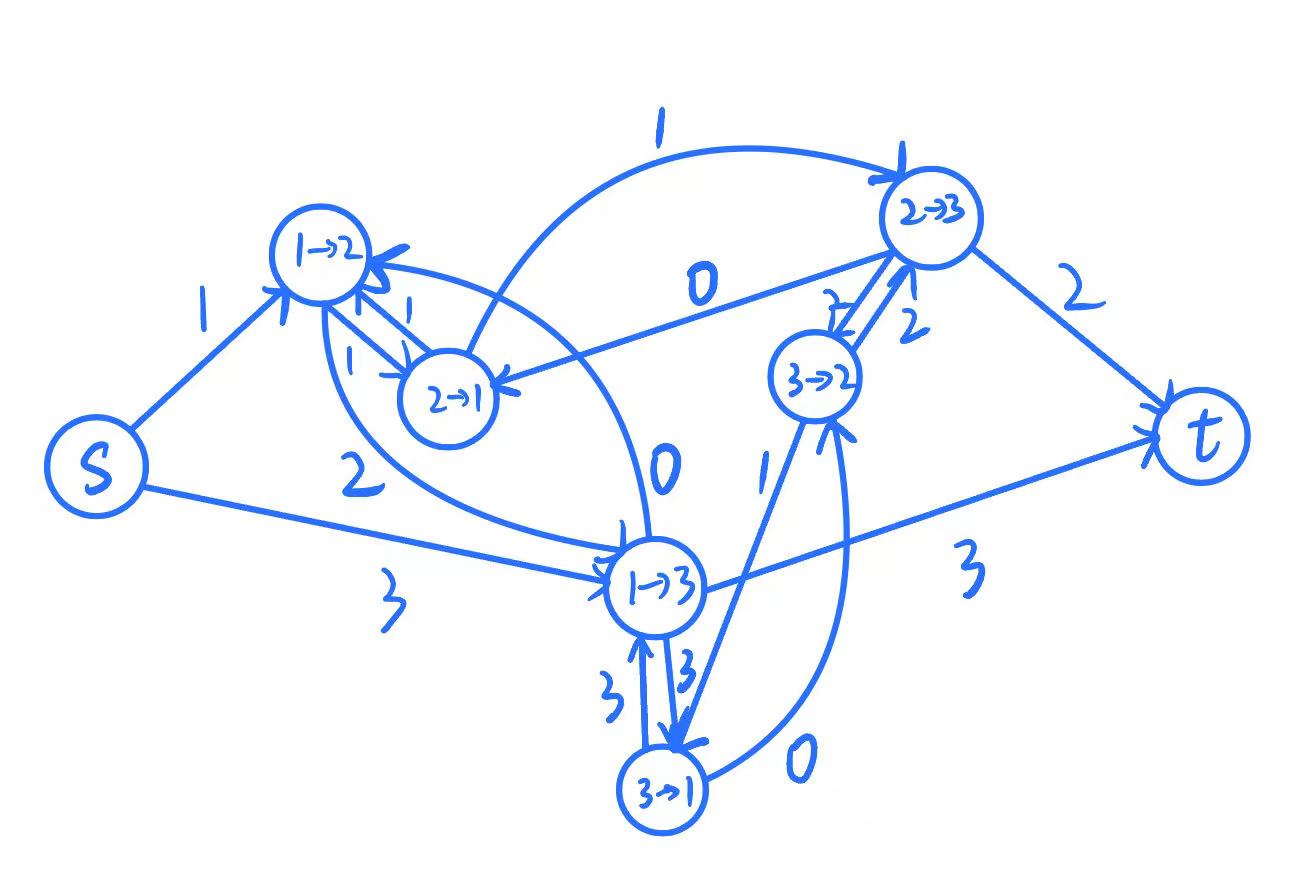
诡异的数据范围.
不过看到这个题应该自然就有根号分治的感觉.
很明显要么 doge 的步长小于 \(\sqrt{n}\), 要么它能到达的位置只有 \(\sqrt{n}\) 个.
我们设置一个阈值 \(W\).
若当前 doge 的步长大于等于 \(W\), 直接连边即可, 设这样的 doge 有 \(x\) 只, 得此时边数为 \(\dfrac{nx}{W}\).
若当前 doge 的步长小于 \(W\), 我们有这样的思路:
不是将 doge 和它能到达的点进行连边, 而是直接对于每个点, 连接双向边 \((u-p,u)\) (设 当前 doge 的步长为 \(p\)). 这样就一次处理完了所有相同步长的 doge.
但是这样做是有问题的. 因为不同步长的 doge 之间会相互影响. (以样例为例, 如下图)
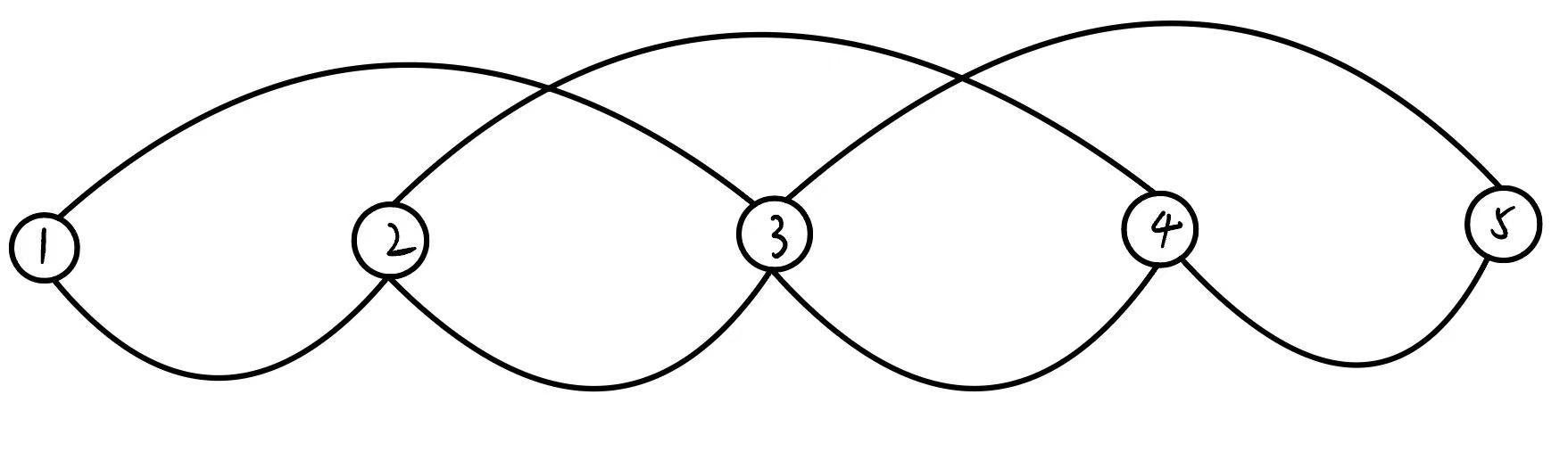
理想: \(1\rarr3\rarr5\rarr4\rarr3\rarr2\)
实际: \(1\rarr3\rarr2\)
所以说我们要建分层图, 像这样:
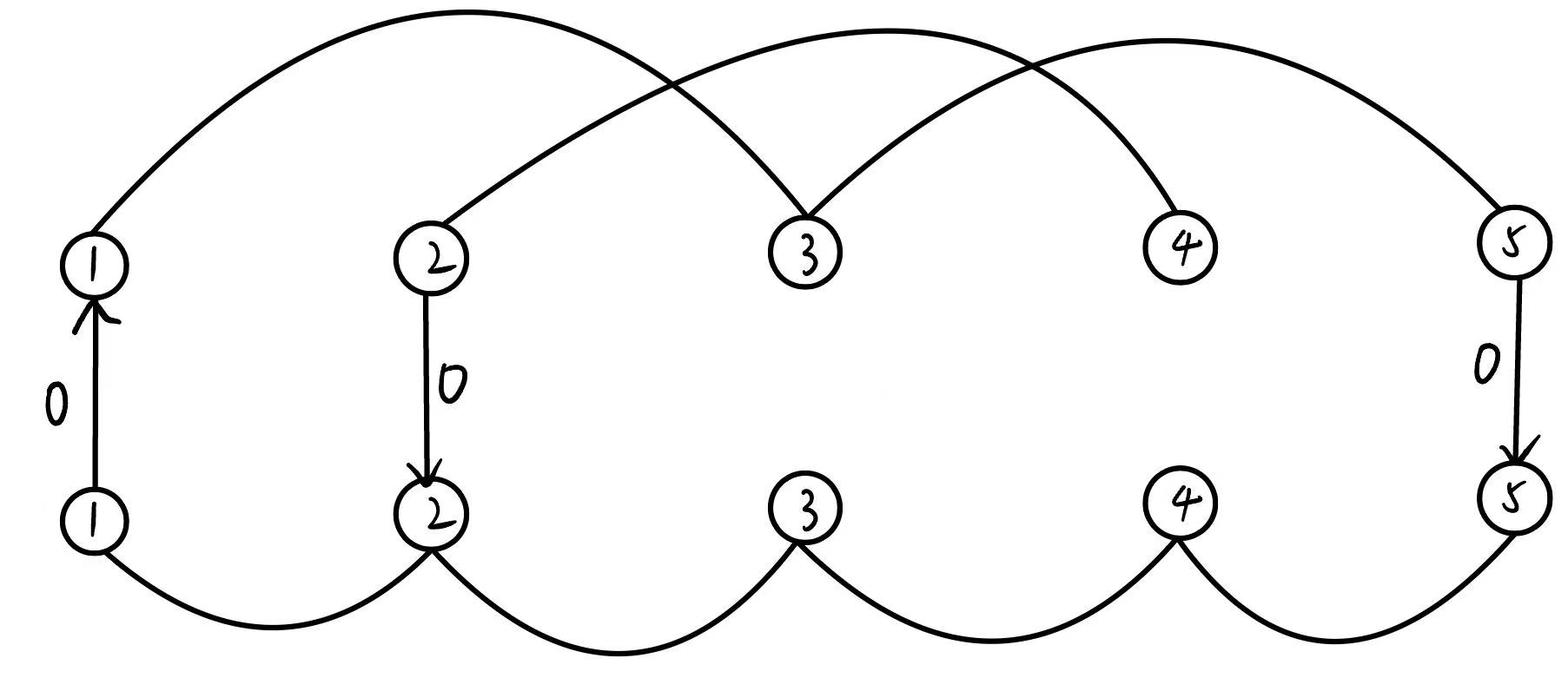
层之间的边表示更换 doge.
容易看出若步长小于 \(W\) 的 doge 有 \(y\) 只, 那么这样建图边数是 \(3yW\).
则总边数为 \(3yW+\dfrac{nx}{W}\geqslant2\sqrt{3nxy}\), \(W=\sqrt{\dfrac{nx}{3y}}\) 取等. 由于 \(x+y=n\), 边数最多为 \(n\sqrt{3n}\), 可以接受.
