平衡树——B树、左偏红黑树和红黑树(待更)
最后我们来介绍B树和其衍生出的(左偏)红黑树。
B树和红黑树的图源自这个网站,你也可以在上面找到一些其他的数据结构。
左偏红黑树的图源自这个slide、OI-wiki(删除操作)和这里。
1. B树
我们发现二叉树做不到绝对平衡。于是我们考虑多叉树。
B 树(也叫B-树)就是一种完全平衡的多叉树,也就是说,每个叶子结点的高度都是一样的。
首先我们先给出一张 B 树的图,并且介绍 B 树的一些基本性质。
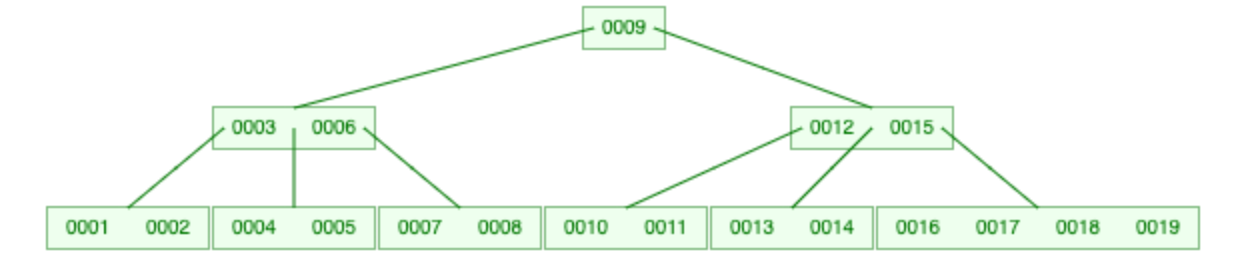
- 一个结点如果有 \(k\) 个索引,那么它就有 \(k+1\) 个孩子。索引和孩子的排列方式与 BST 类似。
- 一个结点不能无限制地拥有索引。若我们称一棵树是 \(m\) 阶 B 树,那么对根结点有 \(1\leqslant k\leqslant m-1\),对其他结点有 \(\left\lceil\dfrac{m}{2}\right\rceil-1\leqslant k\leqslant m-1\)。比如上图是一棵 5 阶 B 树,那么除根节点外,每个节点至少有 2 个索引,至多有 4 个索引。但是根节点的索引可以更少,比如上图的根结点只有 1 个索引。
- 3 阶 B 树也叫做 2-3 树,4 阶 B 树也叫做 2-3-4 树。可以以此类推,但是阶数再高就没人这么叫了。
那么我们接下来就介绍 B 树的相关操作。
只介绍一些前置操作和插入删除,剩下的还是同 BST。
1. split
当一个结点的索引数量过多时,我们需要对这个结点进行 split 操作。
当然这个操作很简单,我们只需要找出来索引的最接近中位数的数,把它提出来就行了。
图示:
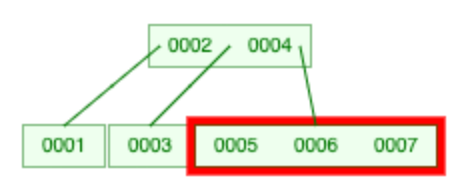
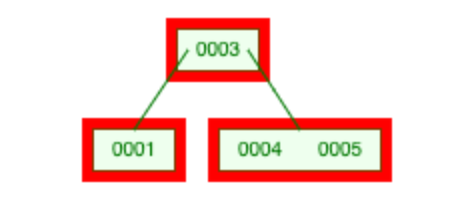
如图是一棵 2-3 树,这个时候我们需要对红框框出的结点进行分裂。我们把 6 提出来:
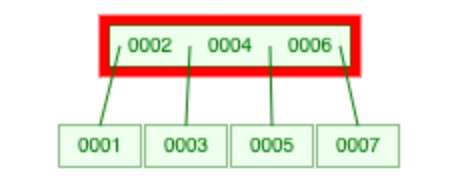
然后我们发现父亲结点又超了。于是继续分裂。
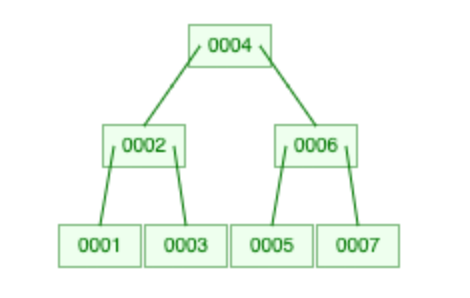
完成。
2. rotate
当一个结点的索引数量过少,并且它的兄弟结点(狭义,仅指左兄弟和右兄弟)的索引数量足够多时,我们使用 rotate 操作。实际操作的时候,我们直接找索引数量多的兄弟结点进行 rotate。
文字描述不方便,直接上图:
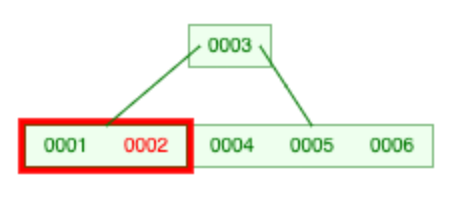
这是一棵 5 阶 B 树。这个地方我们要删除 2,但是删除之后结点的索引个数就过少了。同时我们发现它的右兄弟有足足 3 个索引,即使去掉一个也是满足要求的。于是我们进行这样的操作:
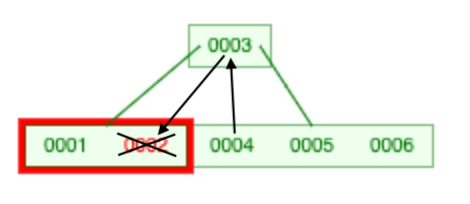
就像左旋一样那我们就叫它左旋好了。
另外一个方向的旋转同理。
3. merge
但是我们会发现,有的时候两个兄弟结点的索引数量都不够。这个时候我们就要进行 merge 操作。
简单地说,就是把左右结点连同索引结点合并成一个结点。因为左右结点的索引数量都足够少,很容易发现合并后的结点不需要再次分裂。事实上,有 \(\left(\left\lceil\dfrac{m}{2}\right\rceil-1\right)+\left(\left\lceil\dfrac{m}{2}\right\rceil-2\right)+1=\left(2\left\lceil\dfrac{m}{2}\right\rceil-1\right)-1\leqslant m-1\)。
还是上图:
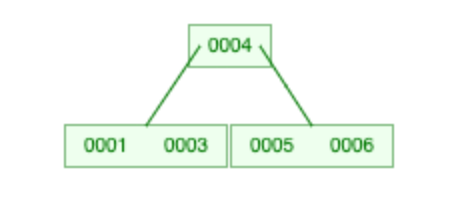
这是一棵 5 阶 B 树。容易发现此时左结点索引数量过少,并且右结点的索引个数也不足以支持 rotate 操作。
于是我们进行 merge 操作,将左右结点和中间的索引进行合并,合并成一个结点。
注意图中的情况比较特殊。因为这个操作拿走了父亲结点的一个索引,所以可能会导致父亲结点的索引数量过少,此时我们还需要对父亲结点进行 rotate/merge,才能保证性质不被破坏。
讲完了前置操作,接下来就是平衡树的正统操作了。
4. insert
学会了 split 之后这个操作应该是显然的。找到对应结点进行插入,如果索引数量过多直接 split 即可。
5. delete
相对应地,delete 操作就复杂许多(连前置操作都是两个)。分类讨论:
- 如果当前结点是叶子结点:直接删除,如果索引个数过少就 rotate/merge。
- 如果当前结点是内部结点:
- 考虑左子树的最大值所在结点,若结点的索引数量足够大那么直接把结点提上来当做新的索引。然后这就是一个删除叶子结点的操作。(右子树同理)
- 如果两个儿子索引个数都过少,则需要先 merge 两个儿子。
- 如果删完之后索引个数还是过少,那还是要 rotate/merge。
内部结点的删除并不是显然的。还是进行图解。
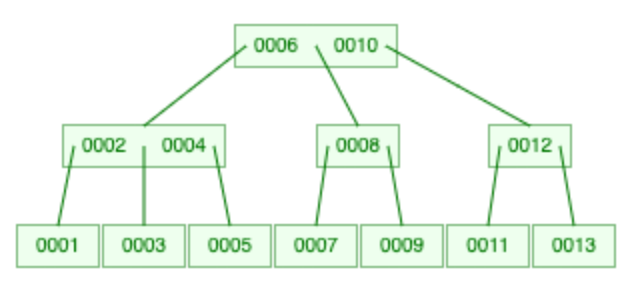
这是一棵 2-3 树。下面我们要删除 6。
我们发现 5 和 7 所在的结点索引数量都不够。那不妨取左边的 5 做一次交换。
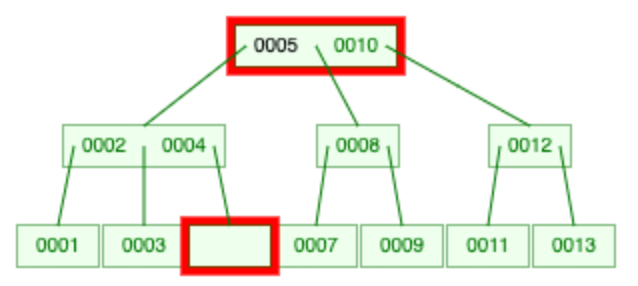
然后接下来就是删除叶节点 5 的操作了。兄弟结点的索引数量过少,考虑 merge,这里就是把 3 和 4 合并。
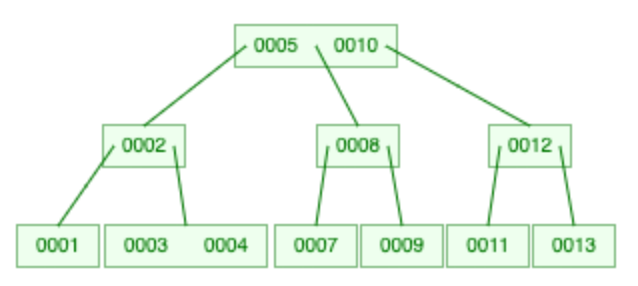
删除操作完成。
在上图的基础上我们再删除 2。容易发现这个时候 3 所在的结点索引数量足够多,因此直接把 3 提上来就行。
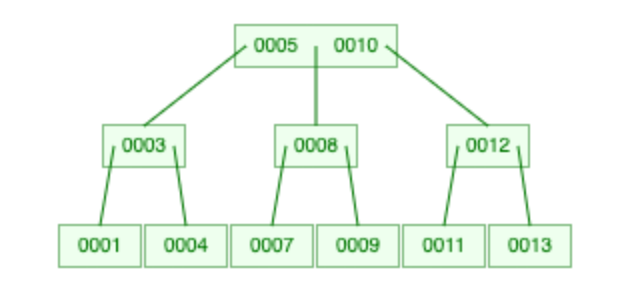
删除完成。
我们再删除 5:
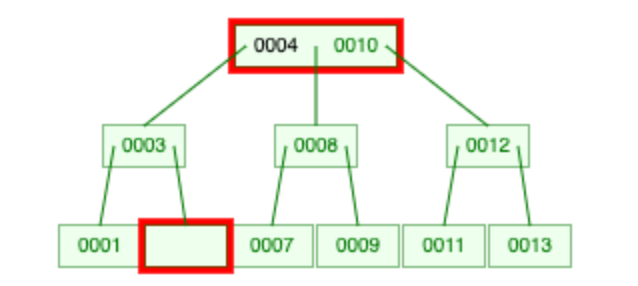
首先交换没有问题。
接下来合并。
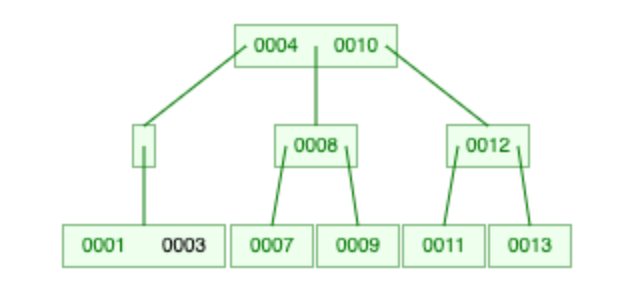
我们发现又出现了一个索引数量过少的结点。
于是再次合并:
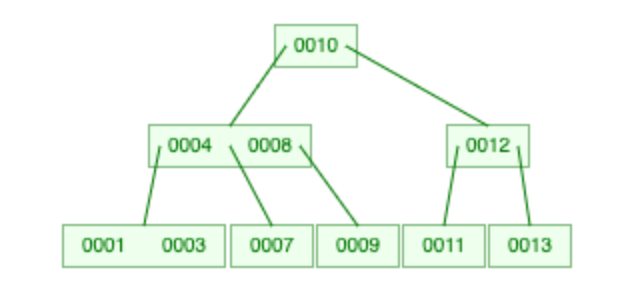
删除操作完成。B树就介绍到这里。
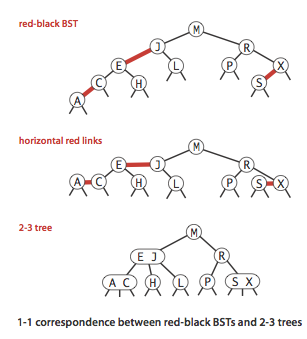
2. 左偏红黑树
B 树好是好,但是写多叉树就不能像二叉树那样好实现。结合两者优点的方法是,将 B 树的结构通过一种对应关系转移到二叉树上。
左偏红黑树(Left Leaning Red Black tree, LLRB)是对 2-3 树的二叉树改造。

如图,我们将一个 3-结点(即索引数为 2 的结点)转化为由红边连结的两个结点,并且规定红边必须左偏。很明显我们不会有连续两条红边。
完整地看:
接下来我们就将 2-3 树的操作挪到 LLRB 上来。
插入:
就是常规的插入操作。插入元素,并连一条红边。
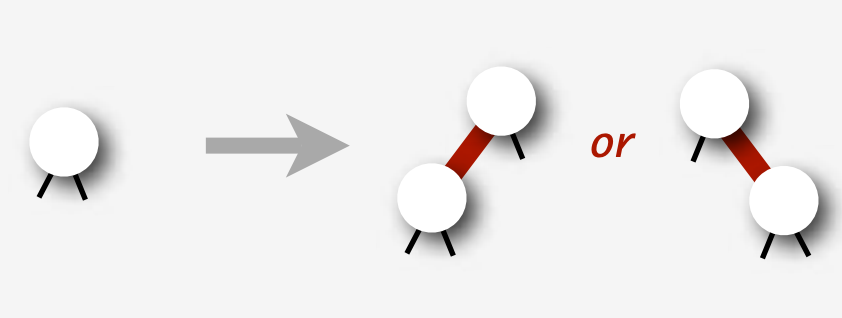
然后通过左旋把右偏的红边改为左偏。

但是可能会出现连续两条红边的情况。我们的操作是,首先做一个右旋把它变平衡,然后反色。
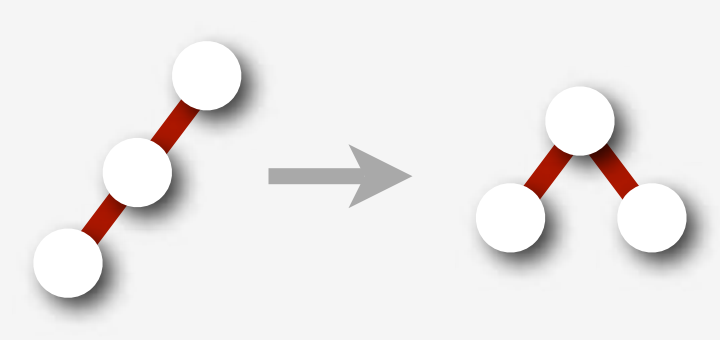
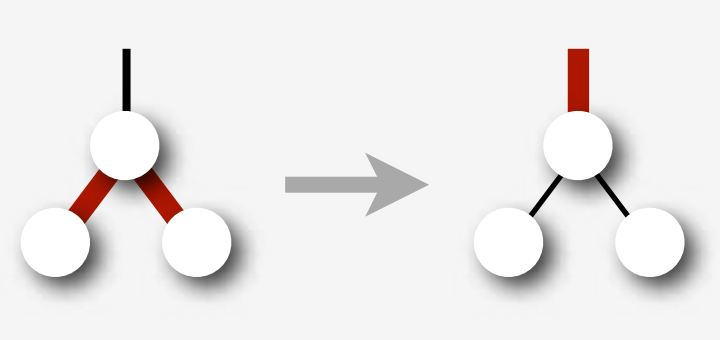
注意上图的操作会影响到上面的结点,可能还会出现连续两条红边的情况,这需要我们递归进行处理。
放一张完整的图:
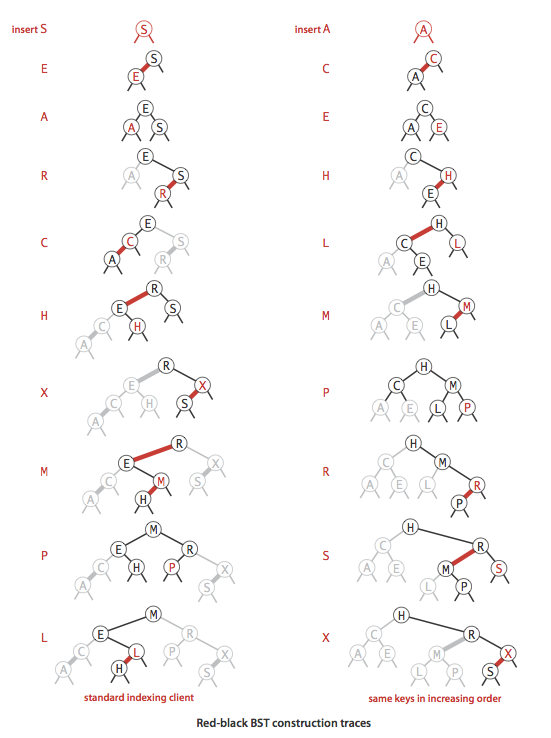
删除:


