笛卡尔树

笛卡尔树就是每个结点有两个值 val 和 key，其中 val 满足 BST 的性质而 key 满足堆的性质。treap 就是一棵笛卡尔树。
可以证明给定 val 和 key 的前提下笛卡尔树的形态是唯一的。
很明显借助于平衡树的知识我们能 \(O(n\log n)\) 进行构建。
但是，当给定的元素已经按照键值 val 排好序了，我们完全可以做到线性。方法如下。

首先，我们注意到由于 val 有序，我们每次插入的位置一定是右链末端。
于是我们有这样的算法：
每次插入一个元素的时候，从下往上与右链中的元素进行比较直到找到位置，然后把原来右链中的结点整体作为当前结点的左子树。
这个过程很明显可以用栈来模拟。注意到每个元素最多入栈一次，于是我们就做到了线性复杂度。

上图。框出的部分就是用栈维护的右链。

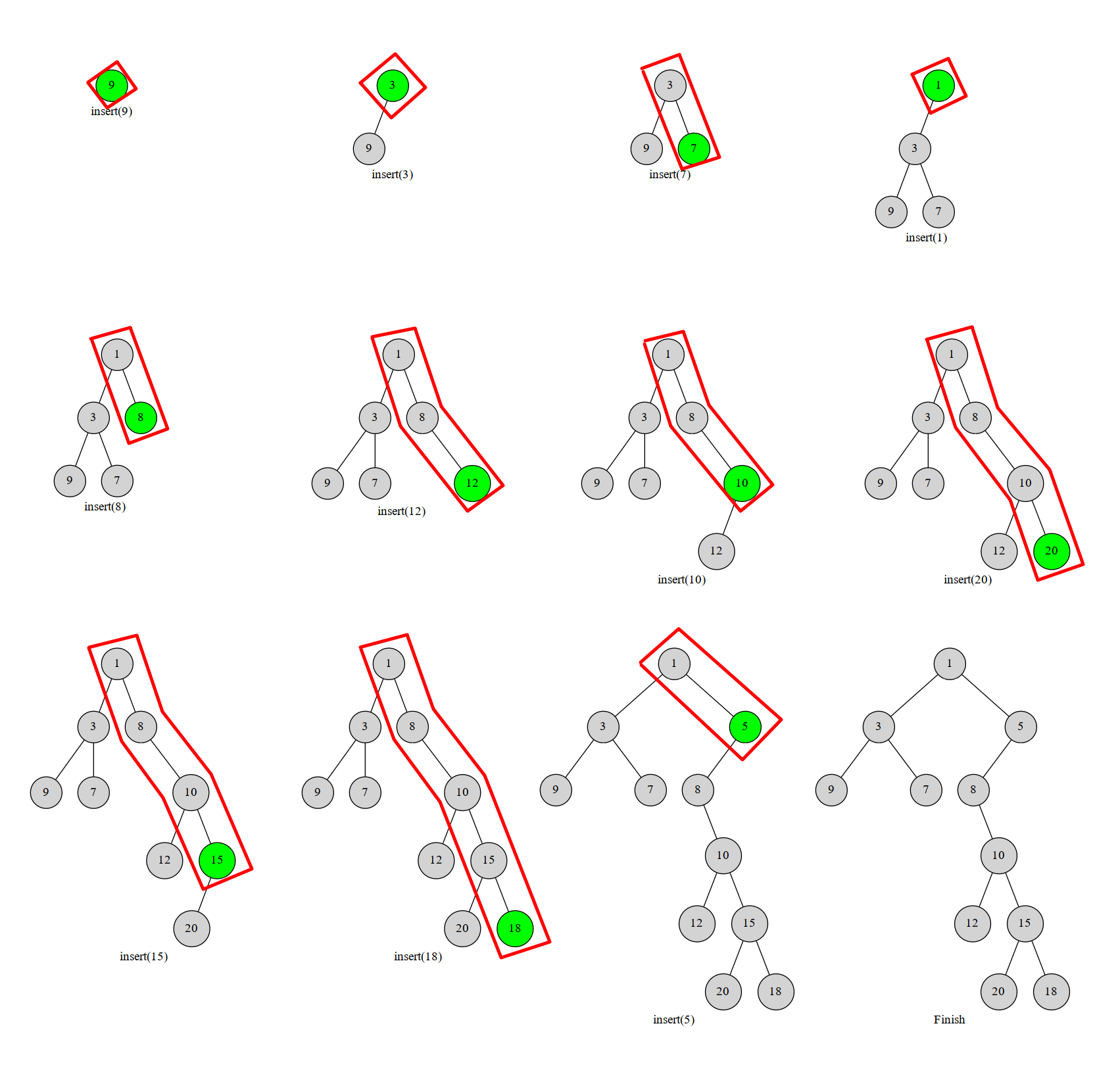
（图源自OI-wiki）

luogu模板题核心代码：
（为了卡常手写了栈

for(int i=1;i<=n;++i)
{
    a[i]=read();
    pos[a[i]]=i;
    if(!top){st[++top]=a[i];continue;}
    int lasttop=0;
    while(top&&a[i]<st[top])lasttop=st[top--];
    if(top)rs[pos[st[top]]]=pos[a[i]];
    st[++top]=a[i];
    ls[pos[a[i]]]=pos[lasttop];
}