平衡树——旋转treap，AVL树和WBLT

fhq_treap 和 Splay 之外的平衡树的代码是不可能写的。仅供学术研究，所以只有口胡，没有代码。

1. 旋转treap

学过 fhq_treap 的都知道 treap 是啥吧（
但是 treap 也可以用旋转来维护。

插入操作：
这是显然的，找到位置插入以后，把结点一路转上去，直到父亲结点的 key 值小于当前结点的 key 值就行了。
容易发现这样旋转没有破坏堆的性质。

删除操作：
如果只有一个儿子那就把儿子转上来，然后到子树进行操作。两个儿子转较小的那个。
配几张图。图中结点处标的都是 key 值。

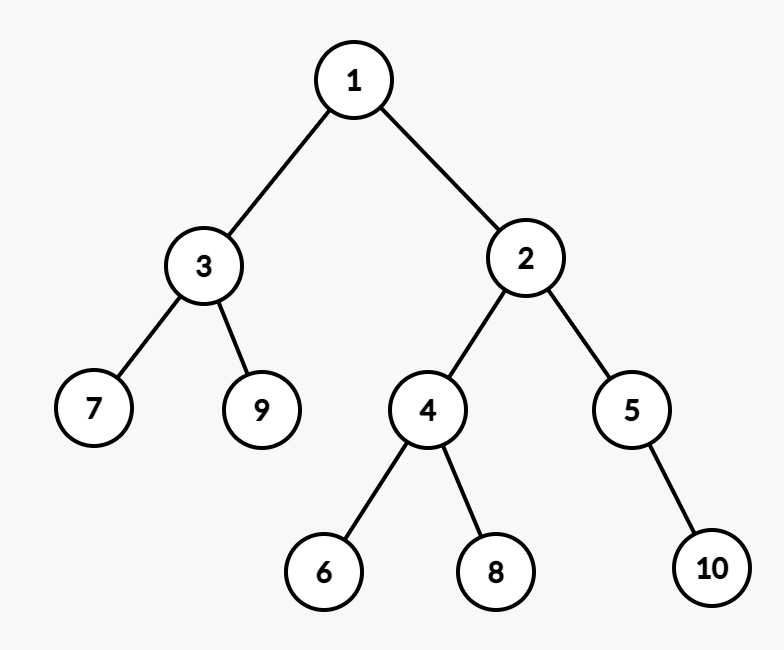
好的我们要删除 2 这个结点。4<5，把 4 旋转上去。

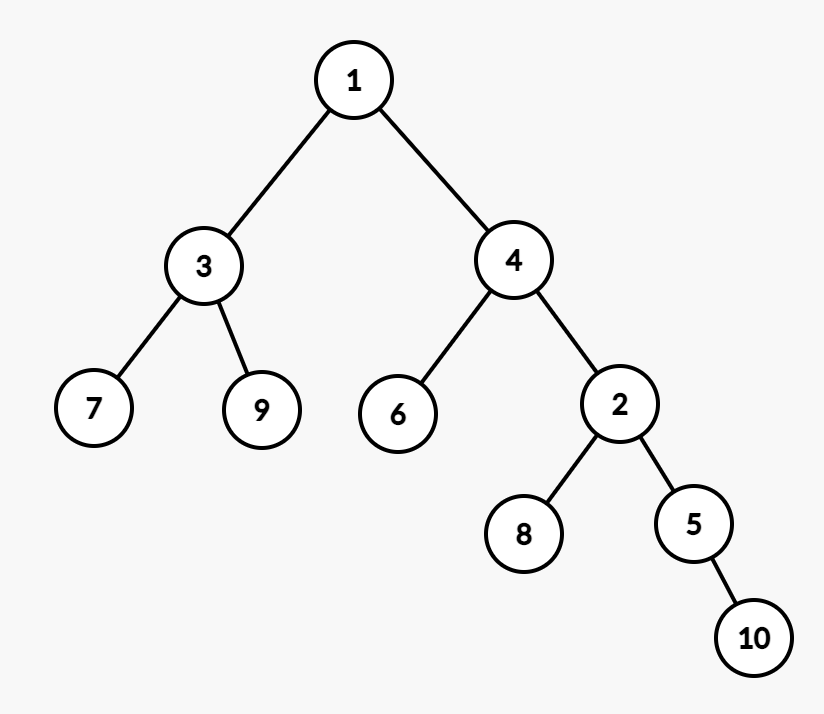
这样 2 就往下了一些。同理，5<8，把 5 转上去。

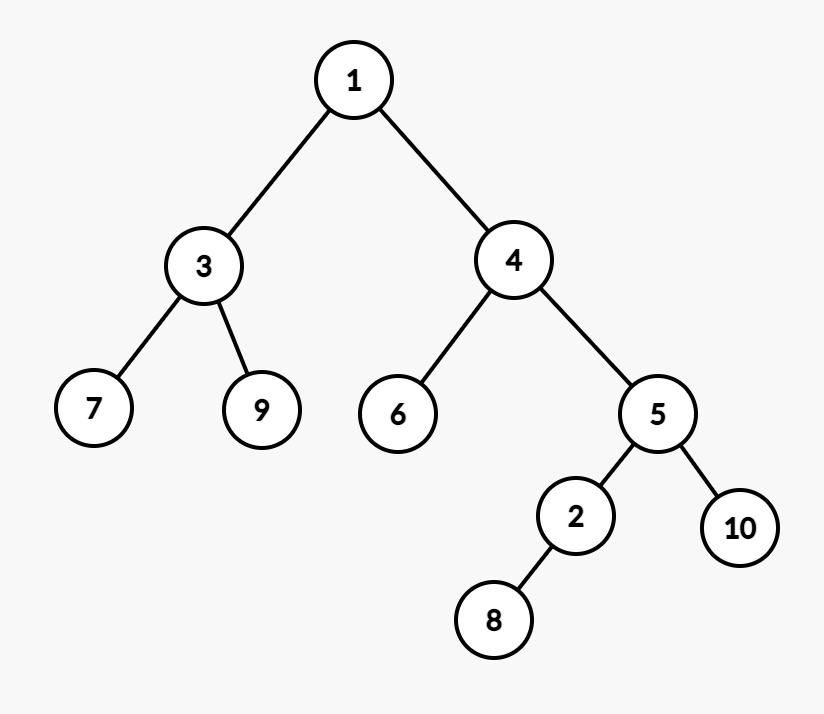
只有一个儿子了。只能转 8。

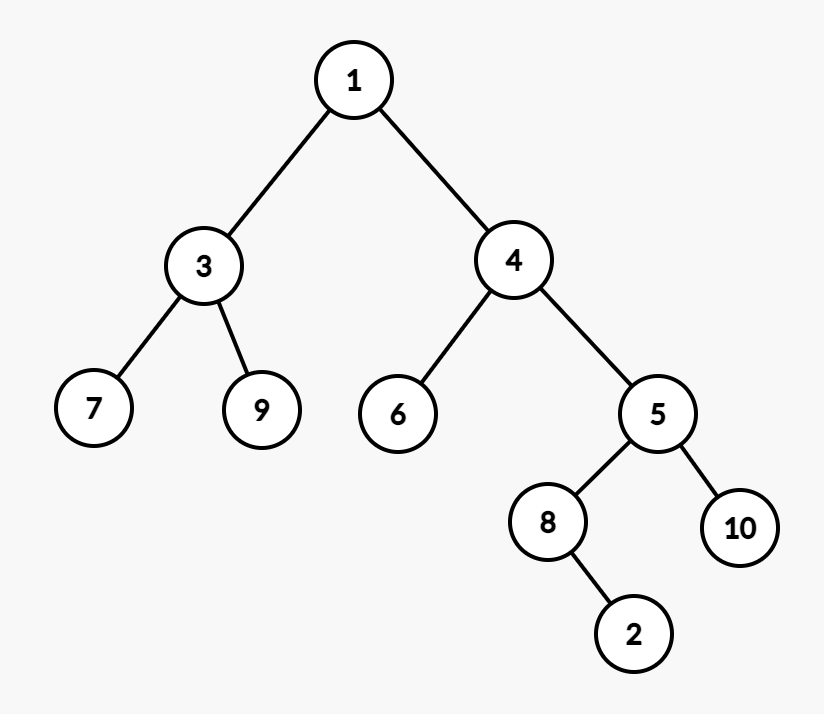
没有儿子结点了。那就可以直接删掉了。

剩下的操作和普通的平衡树就没什么差别了，略。

2. AVL树

这时最古老的一种平衡树，不过因为没什么用所以没人写。
AVL树的思路是让每个结点的两棵子树的高度差的绝对值不超过 1，所以也被叫做高度平衡树。
也就是说，当出现子树高度差的绝对值大于等于 2，即有一个子树过高时，我们就要通过旋转保持树的平衡。
具体分类如下：
LL：左子树过高且左子树的左子树比较高
LR：左子树过高且左子树的右子树比较高
RL：右子树过高且右子树的左子树比较高
RR：右子树过高且右子树的右子树比较高
这里只介绍 LL 和 LR 的处理，剩余两种同理。

LL：

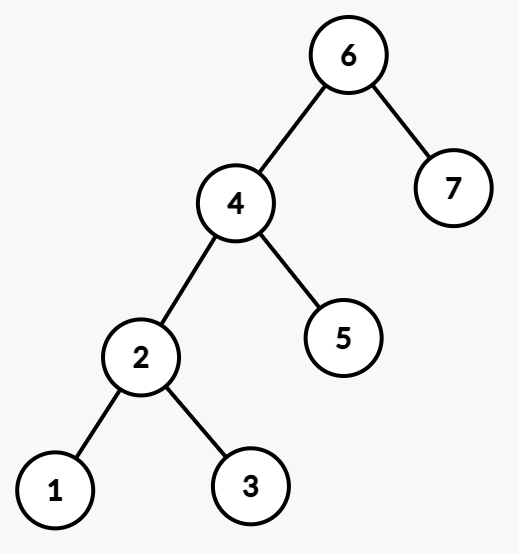
如图所示，6 的左子树就过高了，并且 4 的左儿子比较高。因此这是 LL 的情况。
解决方法非常简单，只需把 4 旋转上去。

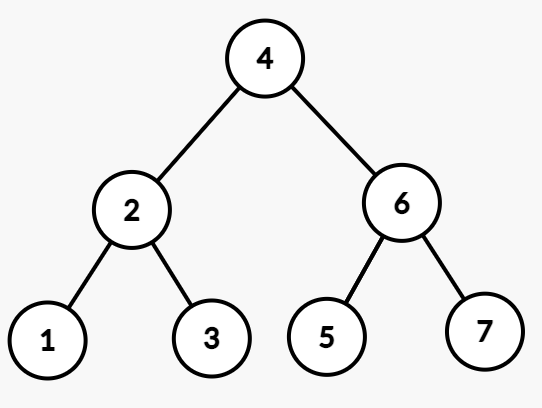
于是就平衡了。

LR：

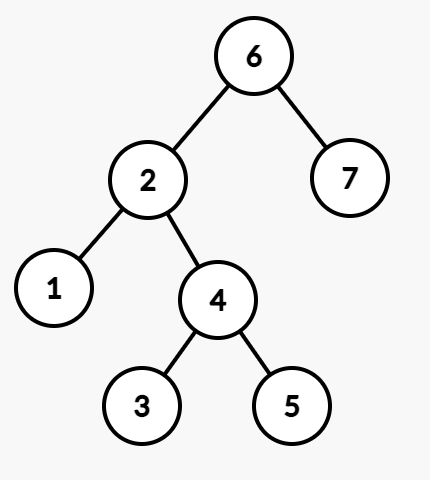
LR 就不能单旋了。方法是，左旋转化为 LL。

然后就简单了。

实际上AVL树就已经讲完了。插入删除等操作同BST，但是要通过上面的操作维护平衡。

3. WBLT

2018年的国集论文里有这个东西。还是非常 interesting 的。
WBLT 全名 Weight Balanced Leafy Tree。Weight Balanced Tree 是大家熟知的，但是这个 Leafy 就比较有趣了。
确切地说，Leafy 是对 BST 进行了一些爆改。
首先这棵树的非叶子结点都有两个儿子。原本的信息都存到叶子结点上，而非叶子结点存储的信息是它的两个儿子的合并。
具体到 WBLT 上，就是非叶子结点的权值和它的右儿子相同。（当然存 size 的时候还是要存子树中有效结点的多少，即叶子结点的个数
但是 BST 的性质还是保留，也就是左子树的叶子结点的值都小于右子树的叶子结点的值。
画个图：

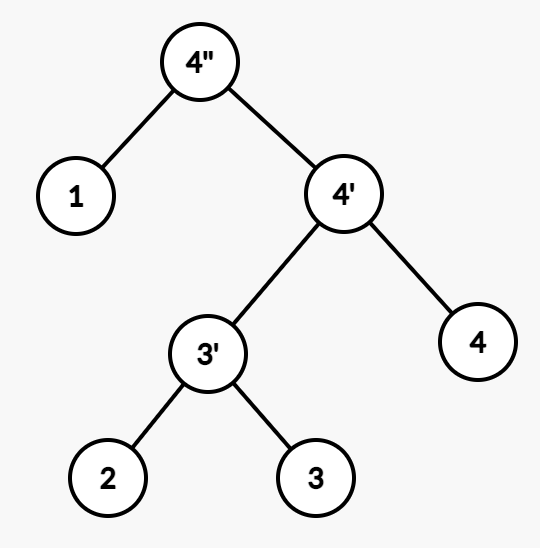
其中 1 2 3 4 就是存储的信息。

接下来我们看这棵树怎么旋转。
还是以上面的树为例，我们做一个左旋，把 4 转上去的操作是这样的：

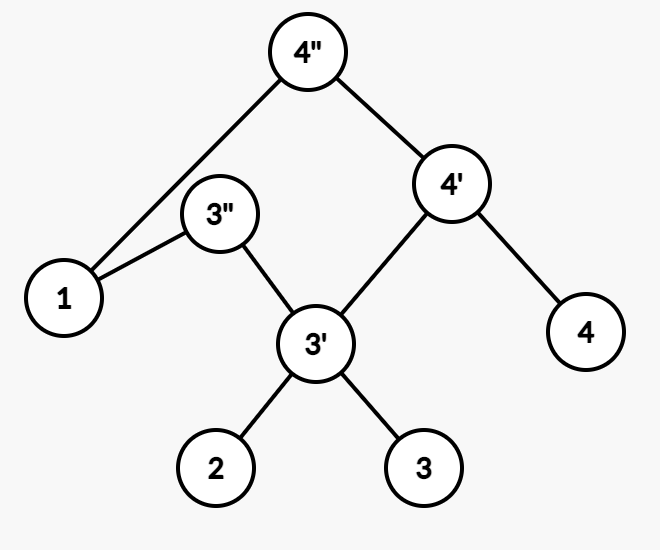
记此时进行旋转的根结点为 x（这里是 4''），左儿子记作 l(x)， 右儿子记作 r(x)。
首先我们新建一个结点合并 l(x) 和 l(r(x))。

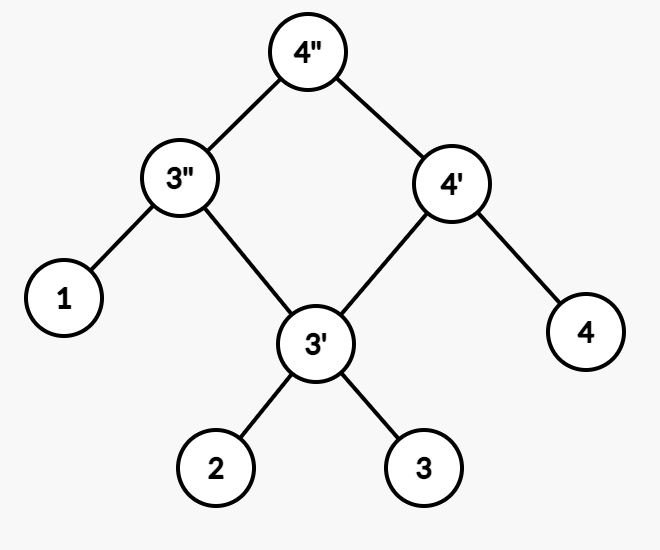
将 l(x) 设为新建的结点。

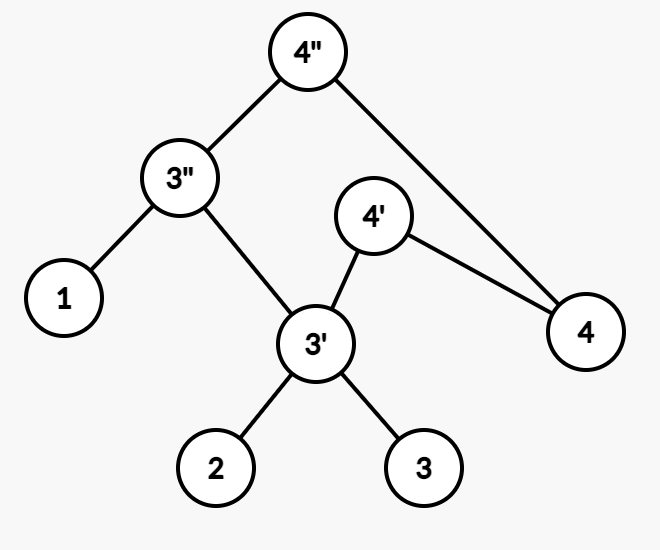
将 r(x) 设为 r(r(x))。
这样就完成了左旋。原来的 r(x) 是不可能被遍历到的，和已经删除无异。（WBLT 中不储存父亲结点）
右旋同理。

然后我们就能用旋转来维护树的平衡了。如果左右子树存储的有效结点个数的比例失调，那么我们就可以通过旋转保持树的平衡。
注：事实上双旋的复杂度才是正确的，但是单旋好像也不容易卡的样子，不过我又不写这个数据结构（

介绍插入删除之前提一嘴，WBLT 的 find 操作和普通的平衡树有一点不一样，那就是要和当前结点的左儿子进行比较，这样才能找到正确的结点。

插入删除：
插入就是递归到叶子结点插进去就行了，然后建立兄弟结点，最后要像线段树一样 pushup 让结点满足 Leafy Tree 的性质。
以上面旋转之后的树为例，我们要插入结点 5。最终结果如下图：

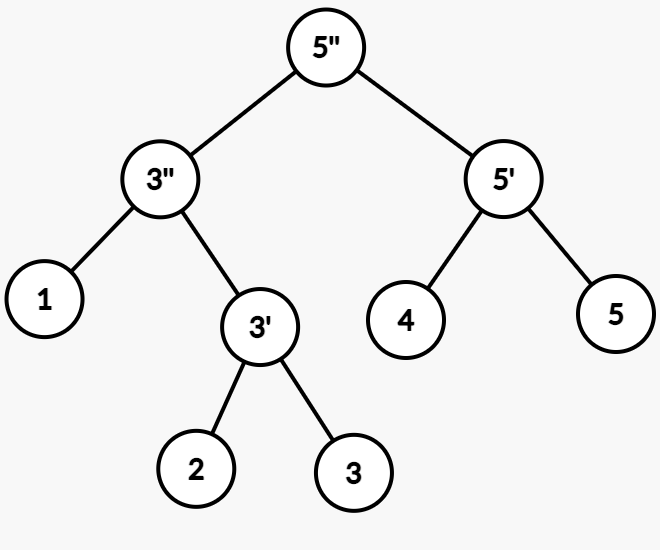
事实上我们就是插入了 5，把 4 挪到 5 的兄弟的位置，然后 pushup 的时候把上面的值都改成了 5。
删除也差不多。注意维护好 Leafy Tree 的性质就行。

剩下的操作略，注意结点存的 size 是子树中叶子结点的多少。