回文自动机

1. 回文自动机介绍和结构

回文自动机，又称回文树，是一个能够存储字符串中所有回文子串的数据结构。
首先放一张图来感受回文自动机的总体结构。这是对字符串 \(\texttt{eertree}\)构建的回文自动机。
（eertree是回文自动机最初提出时的名字，图片来自于原论文）

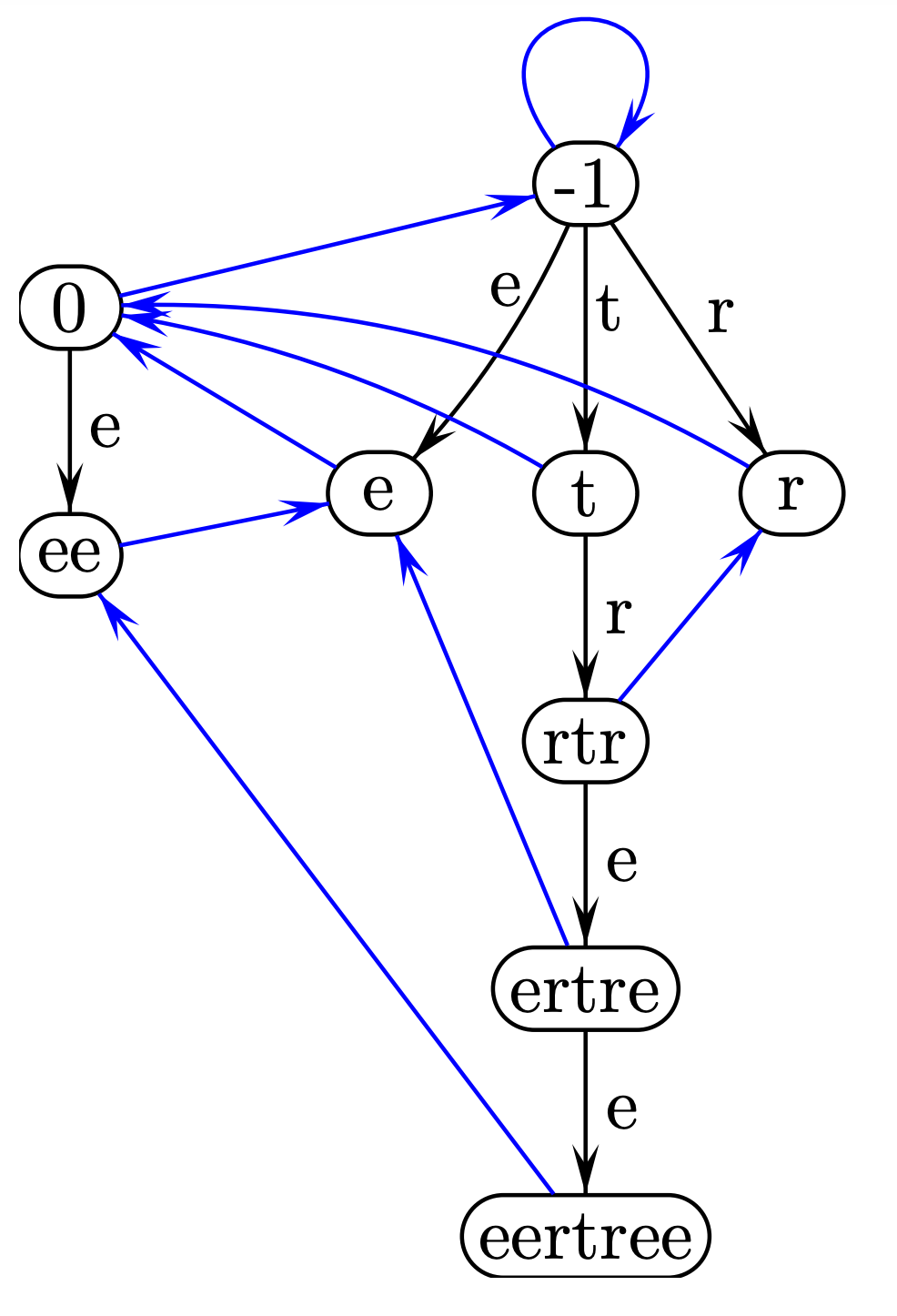
可以看出，有以下几个特点：

回文自动机由两棵树和一堆fail边组成。
一棵树的根的长度是 \(0\)，称为偶根；另一棵树的根的长度是 \(-1\)，称为奇根。（这样定义当然是为了方便）
回文自动机中每个结点表示一个回文串（奇根和偶根除外）。
奇回文串在奇根所在树上，偶回文串在偶根所在树上（废话
从上往下，回文自动机中普通边的意义为在字符串两侧各加入的字符。（奇根与其儿子之间的边除外）
fail指向结点所表示的回文串的最长回文真后缀的对应结点。这一条与AC自动机中的fail边有异曲同工之妙。
人为规定没有最长回文真后缀的fail指向 \(0\)，\(fail(0)=-1\)，\(fail(-1)\) 意义不大。
从本质上来说，应该有 \(fail(-1)=0\)。这样我们才能够将回文自动机定义为DFA，具体如下：

回文自动机是一个接受且仅接受某个字符串的所有回文子串的中心及右半部分的DFA。
“中心及右边部分”在奇回文串中就是字面意思，在偶回文串中定义为一个特殊字符加上右边部分。
这个定义看起来很奇怪，但它能让 PAM 真正成为一个自动机，而不仅是两棵树。
......
为了让 PAM 符合自动机的定义，可以在概念上从-1到0连一条特殊字符边，然后以-1作为起始状态。然而在代码实现里没有人会这么做。
——ouuan

原论文中定义 \(fail(-1)=-1\) ~~是因为原论文并没有将其视为自动机。~~
但是在我们眼中它确实是一个自动机，所以说接下来我们都会以自动机的语言进行叙述。

2. 回文自动机的基础构建法

这里我们介绍回文自动机的基础构建法，并且只介绍基础构建法。
基础构建法的时间复杂度是均摊的，但是已经够用了。
CTSC2017国家候选队论文集《回文树及其应用翁文涛》中对构建法有更深入的讨论。

首先我们给出字符串回文子串的一个性质：
字符串 \(s\) 最多有 \(|s|\) 个本质不同回文子串。
我们可以这样考虑：每次在字符串之后增加一个字符，最多会增加一个本质不同回文子串。
如果增加了多个，取最长的一个回文子串，将剩下的回文子串按照其中心对称一下，就得到了已经在原字符串中出现过的回文子串，矛盾。
这就说明了回文自动机的状态数是 \(O(|s|)\) 的。
另外，在原字符串之后增加一个字符，如果增加一个本质不同回文子串，那么这个子串一定由原字符串的一个回文真后缀向两侧扩展这个字符得到（显然）。
这对应到回文自动机上，就是向下进行了一次转移，增加了一个新的状态。
有了这个性质，我们就可以给出我们的基础构建法了。

基础构建法是一种增量构造法，即每次我们新向回文自动机中添加一个字符进行处理。
首先我们明确，在回文自动机中fail边也组成了fail树。我们接下来的操作大部分都与fail树紧密相关。
假设在添加这个字符前，上一次的状态为 \(u\)，现在轮到字符 \(s_i\)。我们规定在第一个字符上一次的状态为偶根。
记状态 \(v\) 对应回文子串的长度为 \(l_v\)。
我们接下来就根据上面的性质，尝试向 \(u\) 及其回文真后缀前后添加字符 \(s_i\)。
也就是说，我们在 \(u\) 的fail链上，从下往上找到第一个满足 \(s_i=s_{i-l_v-1}\) 的状态 \(v\)，则当前状态为 \(\delta(v,s_i)\)。
如果这个状态不存在，我们还需要连fail边。
连fail边的操作是相似的。我们从 \(fail(v)\) 开始沿fail链寻找第一个满足 \(s_i=s_{i-l_w-1}\) 的状态 \(w\)，则有 \(fail(\delta(v,s_i))=\delta(w,s_i)\)。
若 \(l_u=-1\)，我们还需要特判一下，令fail边指向偶根。

上面的文字描述十分抽象，我们还是要画图来进行理解。以字符串 \(\texttt{aabbaabaa}\) 对应的回文自动机的构建为例。
主要注意右边的fail树，左边回文自动机（省略fail边）跟随其更新。fail树上绿色表示上一次的状态；红色表示当前。

初始：

插入第一个字符。偶根前后加 \(\texttt{a}\) 被否，跳fail到奇根。

发现奇根满足要求，插入结点。fail指针根据特判指到偶根上，同时更新fail树。

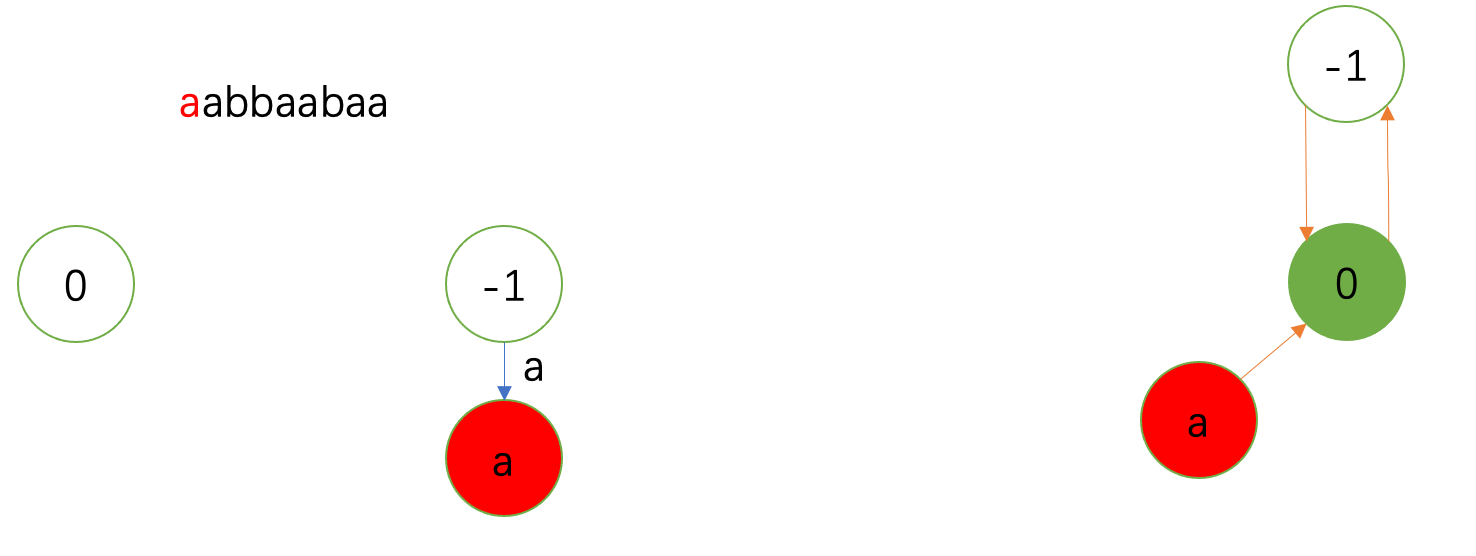
插入第二个字符。\(\texttt{a}\) 前后加 \(\texttt{a}\) 被否，跳到偶根发现成立，插入结点。

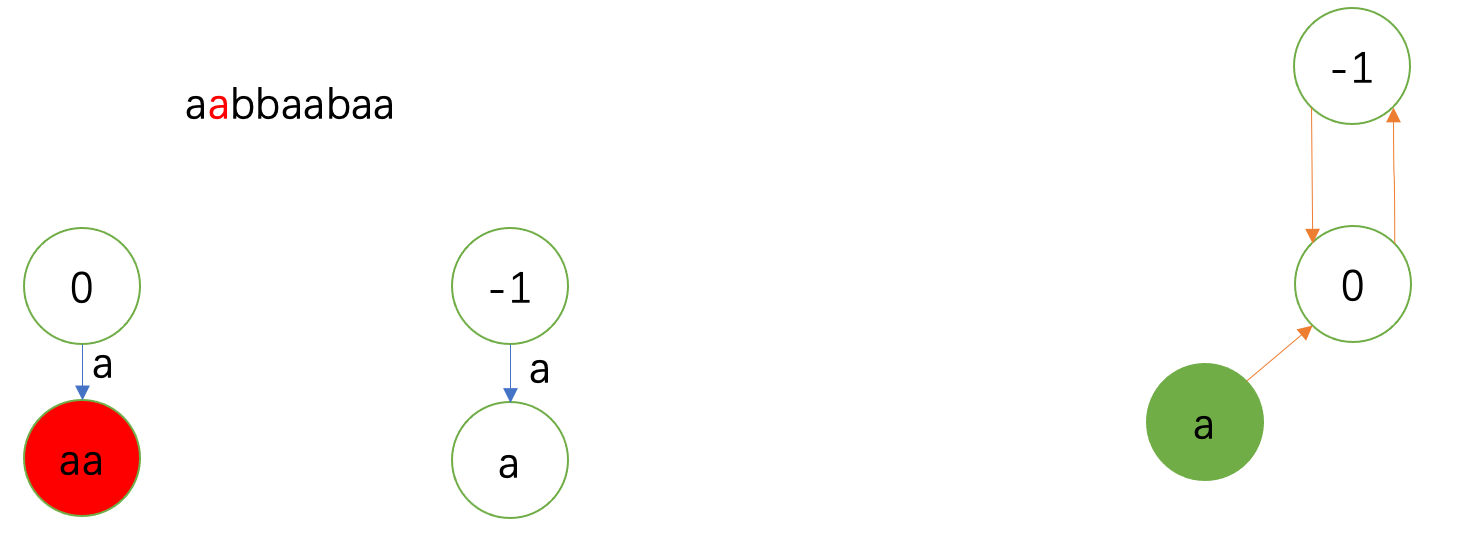
沿 \(0\) 开始第一个满足的就是 \(0\)。于是 \(fail(\texttt{aa})=\delta(0,\texttt{a})=\texttt{a}\)。

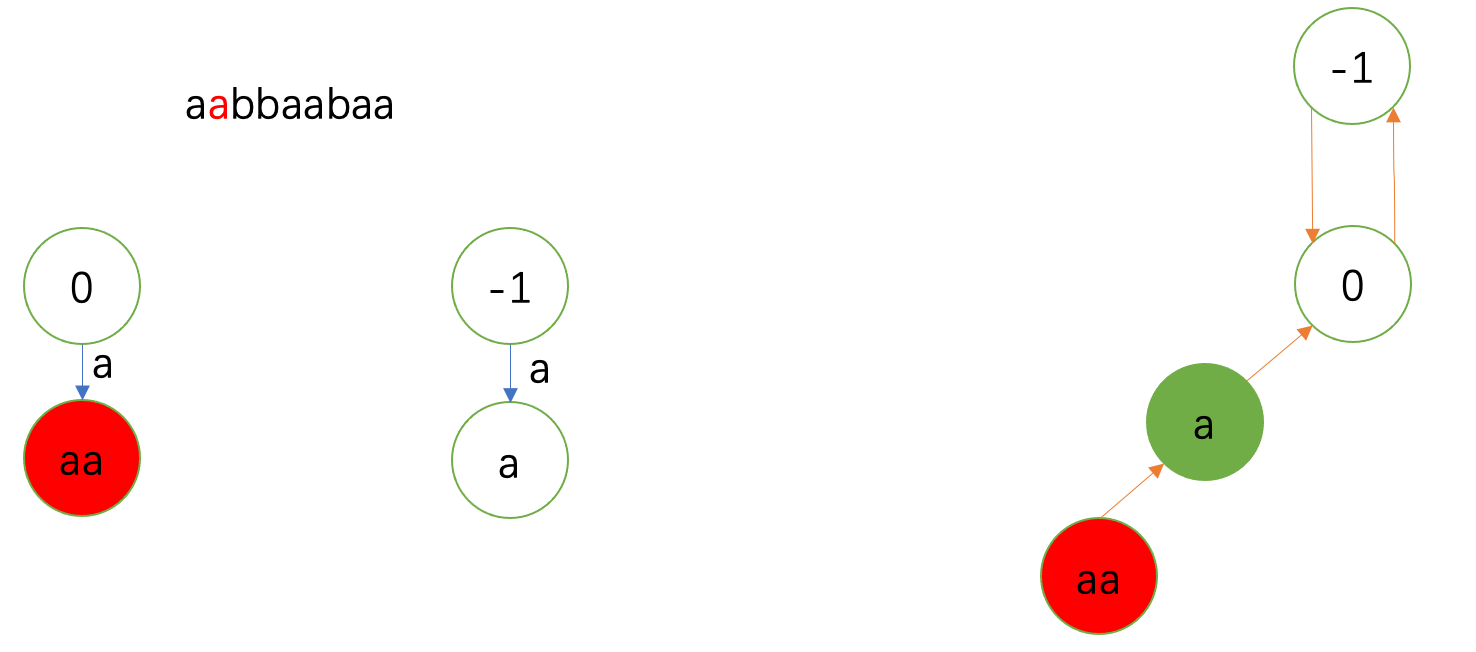
新插入的 \(\texttt{b}\) 一路失配到 \(-1\)，fail边连 \(0\)。

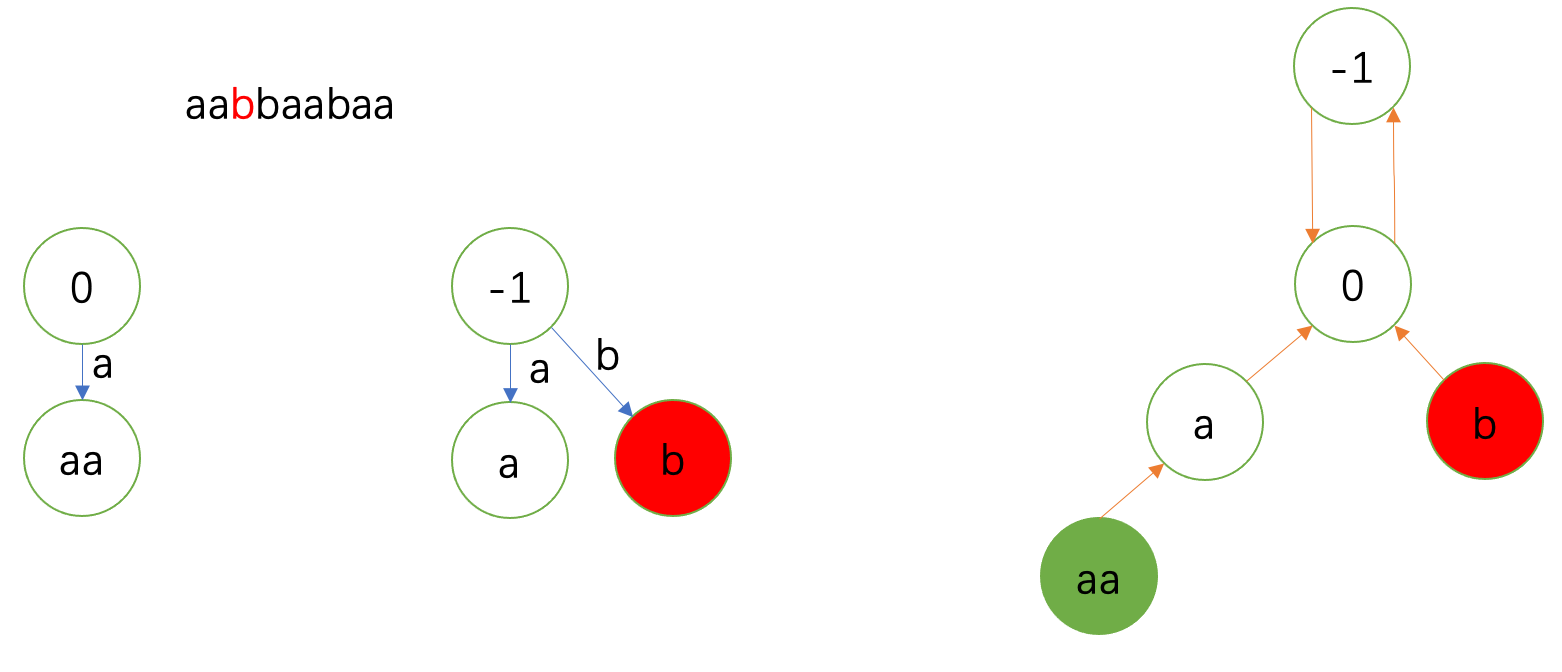
下一个 \(\texttt{b}\) 和第二个 \(\texttt{a}\) 差不多。

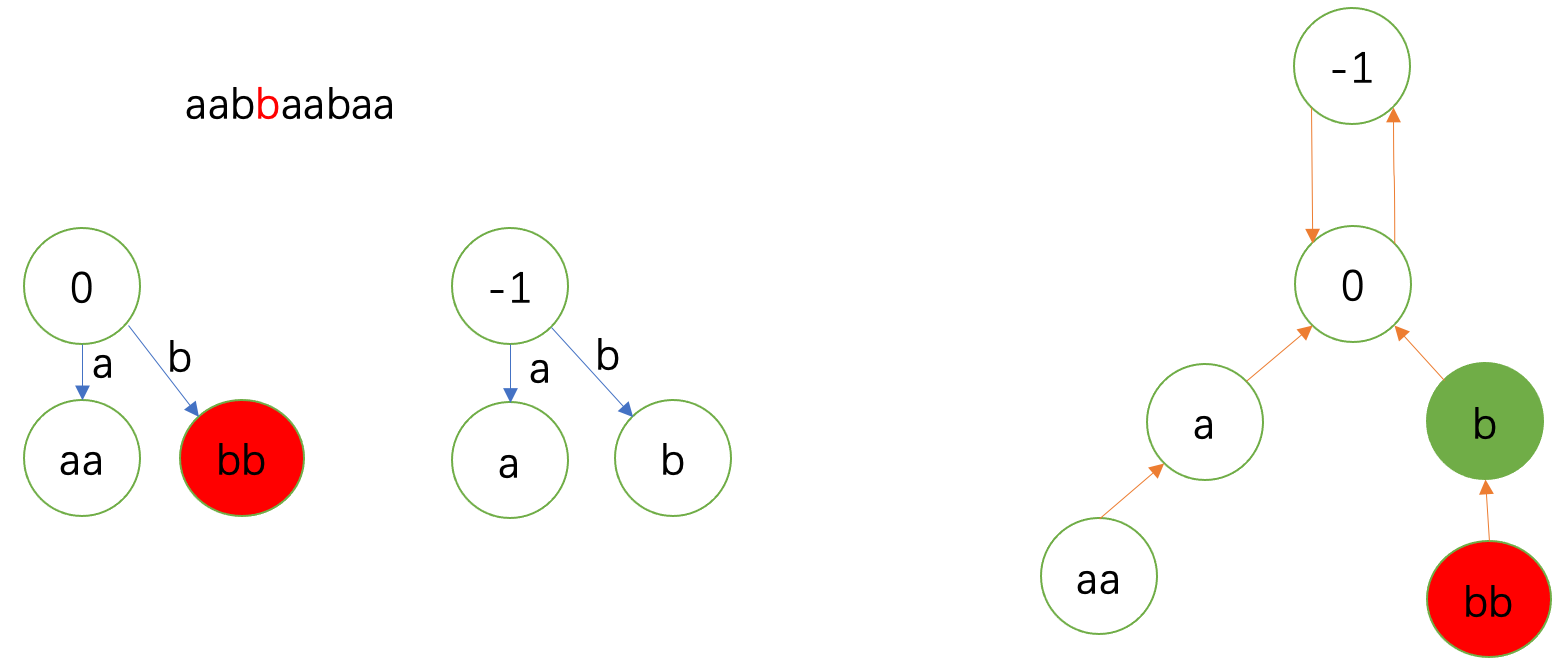
接下来的 \(\texttt{a}\) 分成两张图。
首先是插入，显然在 \(\texttt{bb}\) 就匹配上了。

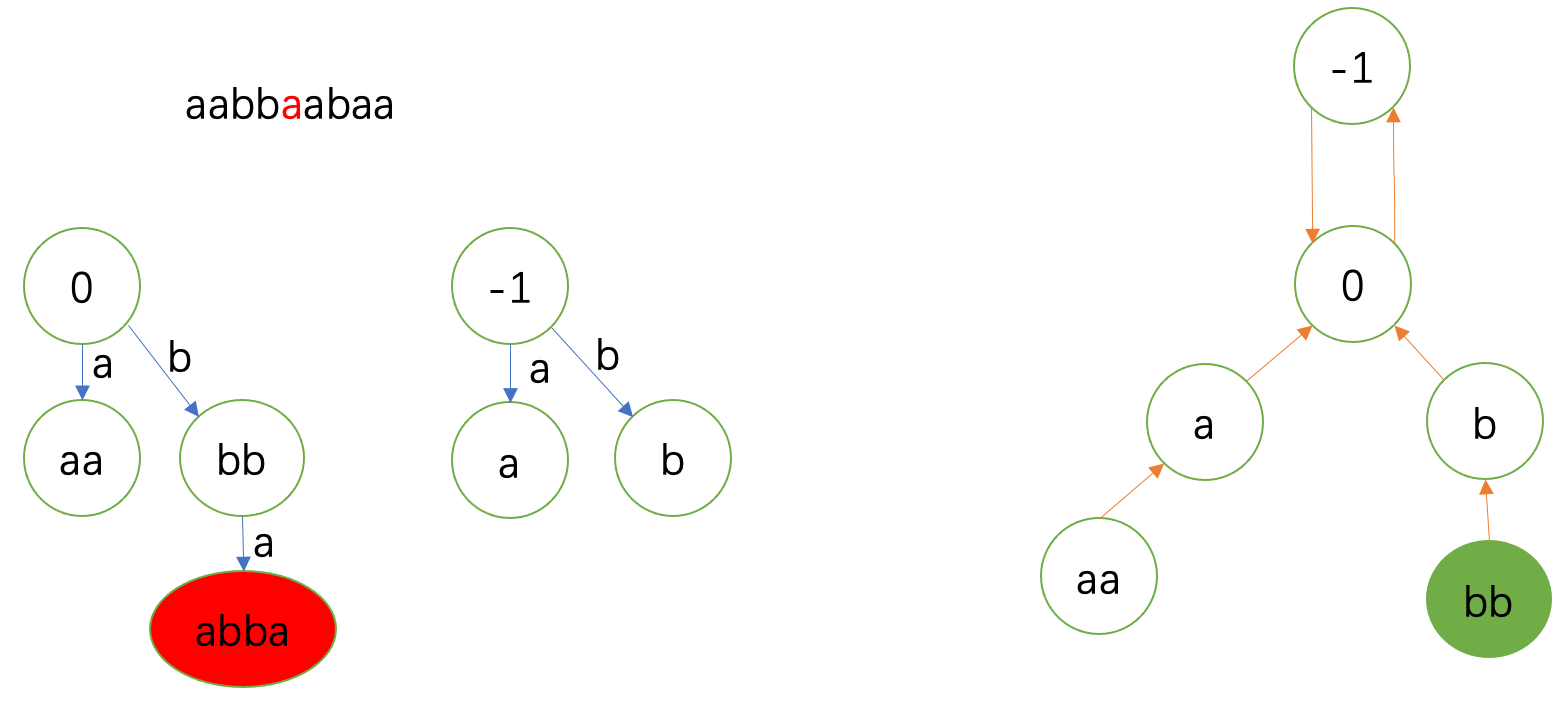
fail指针到 \(-1\) 才实现匹配。于是连到 \(\delta(-1,\texttt{a})=\texttt{a}\)。

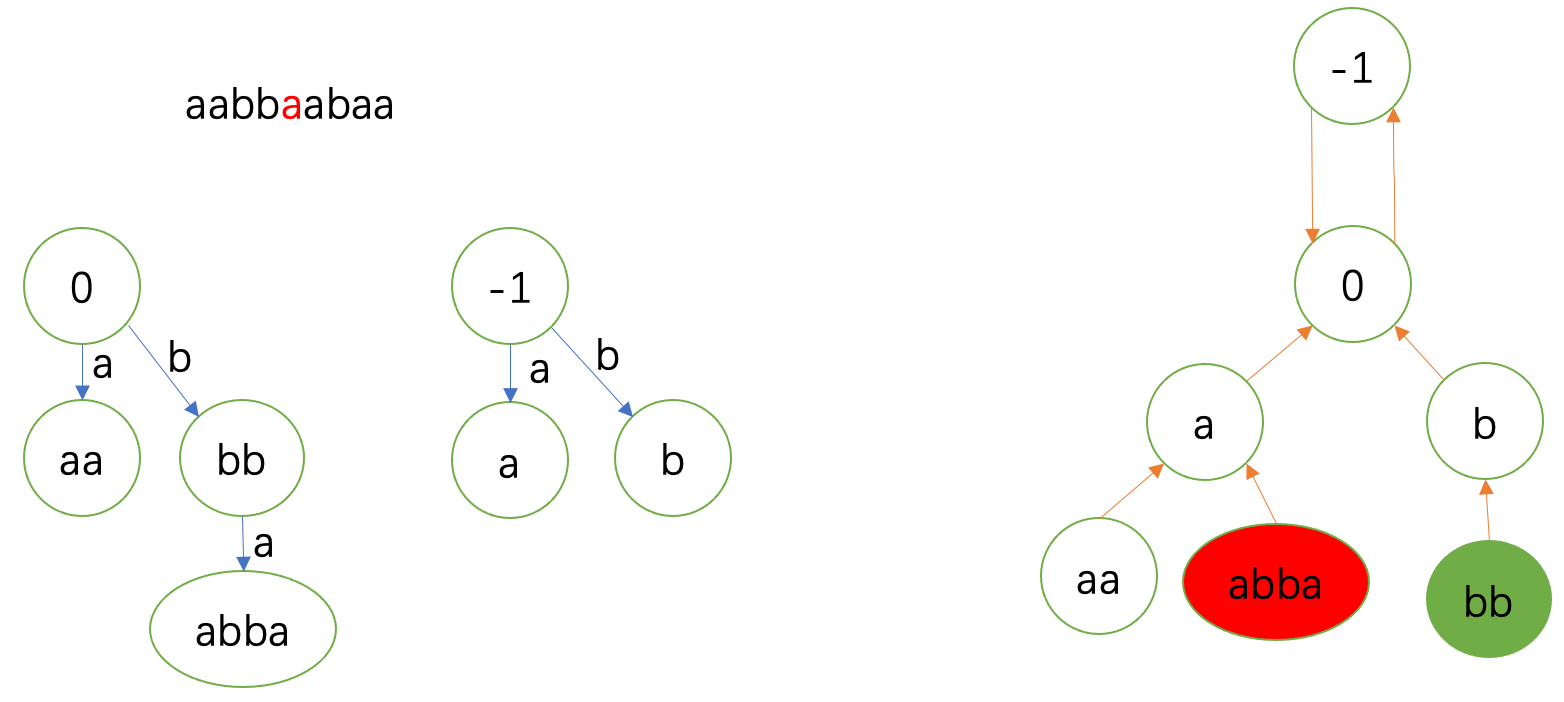
第四个 \(\texttt{a}\) 一开始就匹配上了。

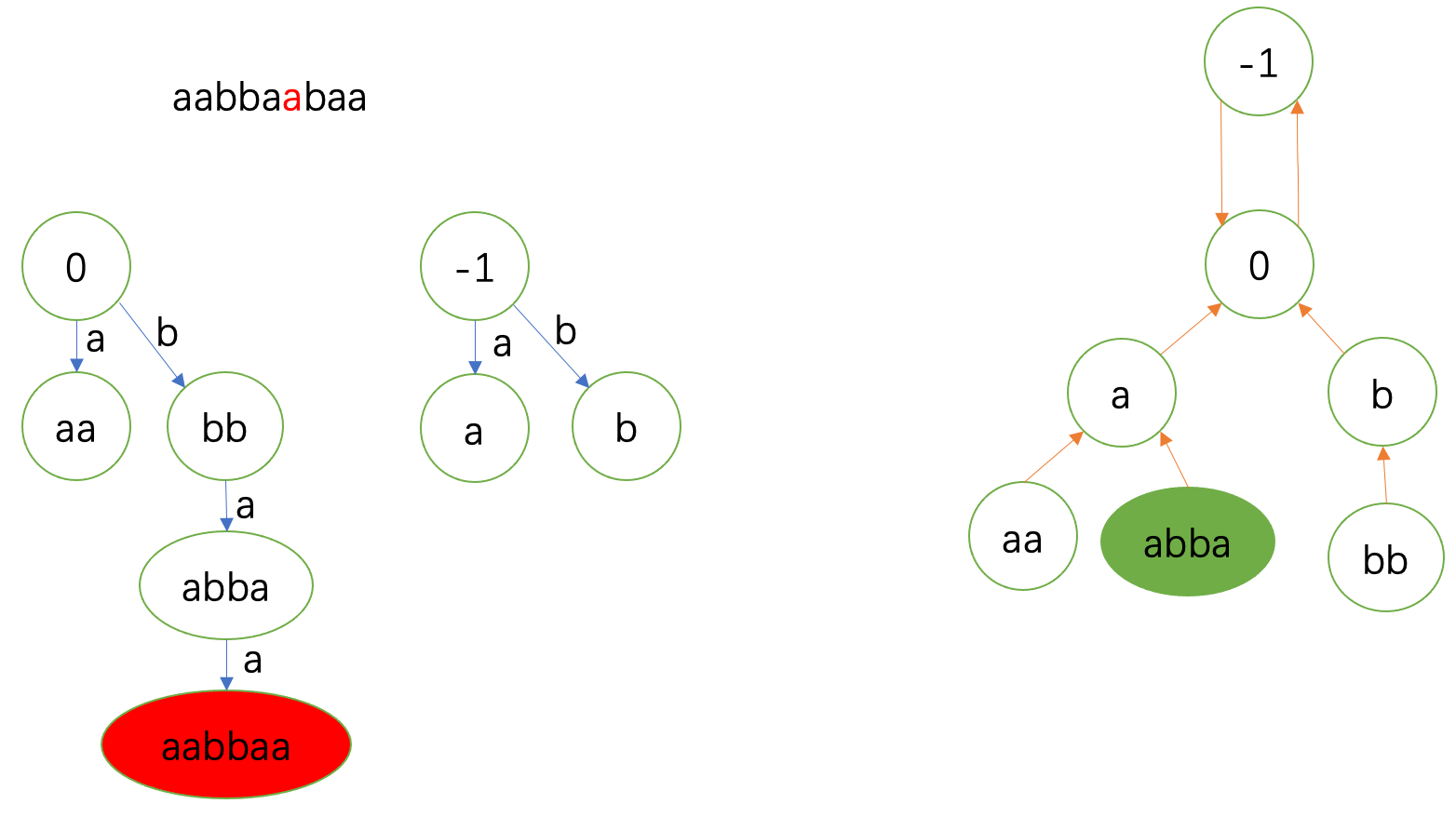
fail指针到 \(0\) 就实现匹配。于是连到 \(\delta(0,\texttt{a})=\texttt{aa}\)。

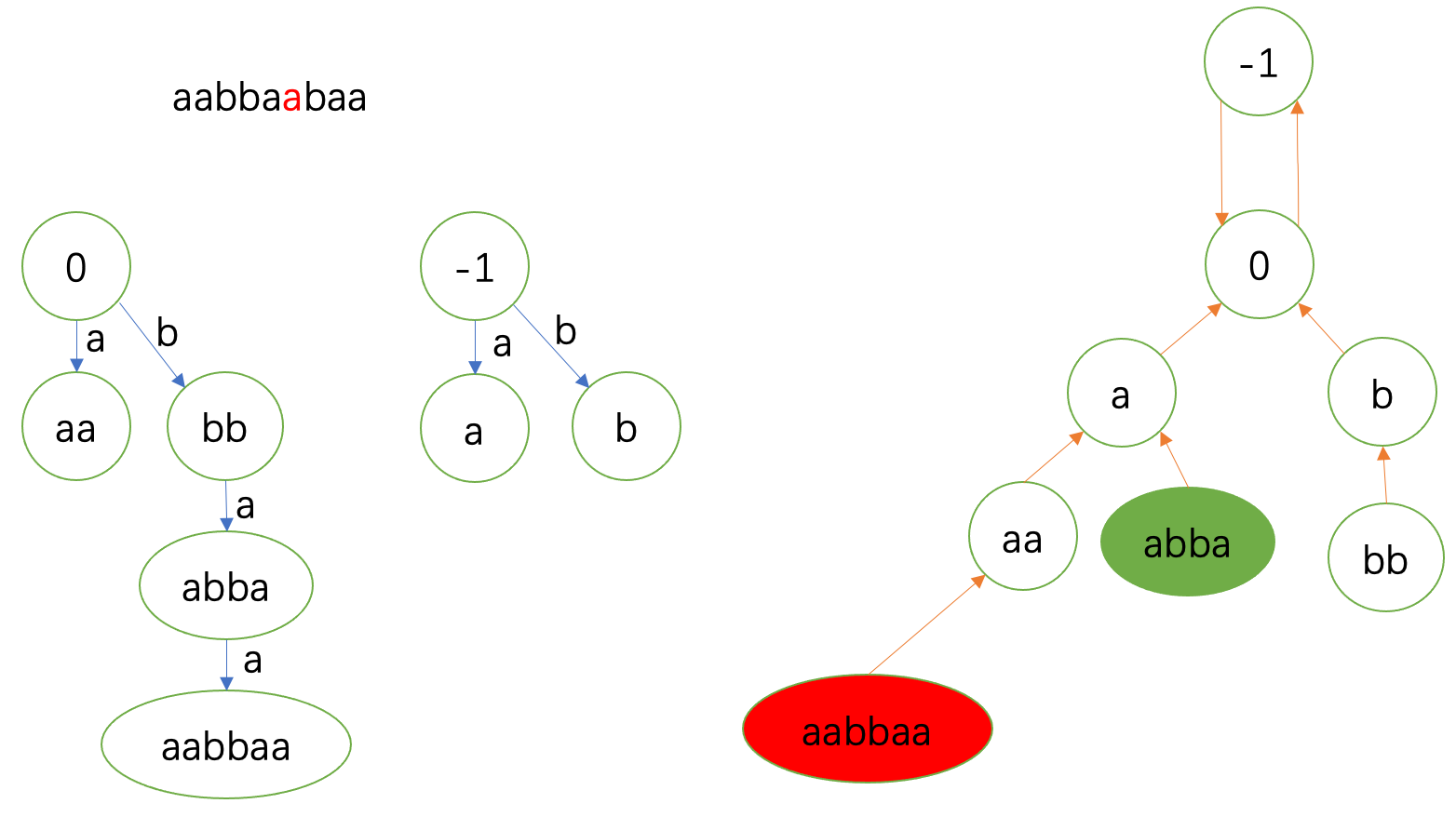
下一个 \(\texttt{b}\) 在 \(\texttt{aa}\) 处匹配。

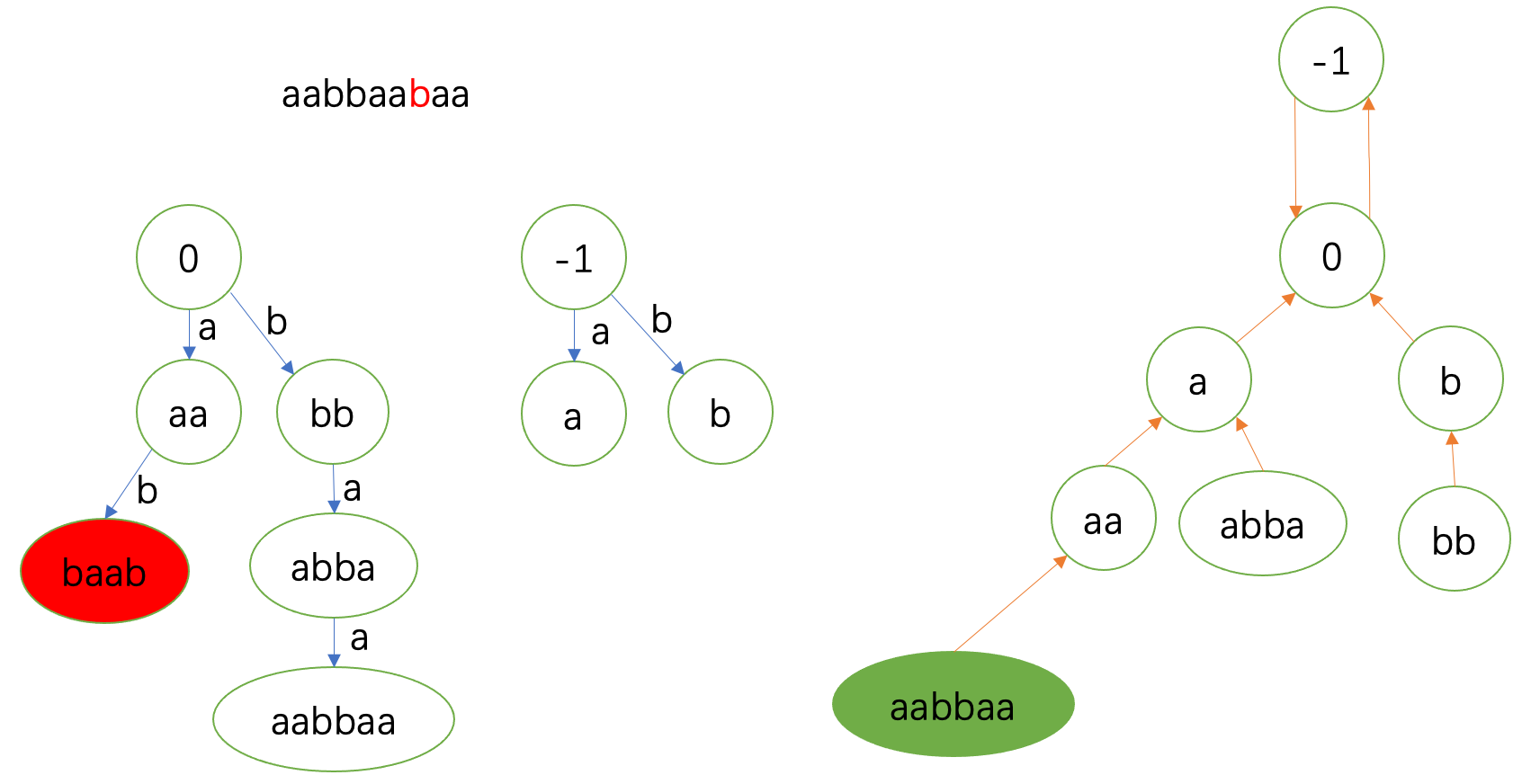
注意了，上面说过连fail边的操作是从 \(fail(v)\) 开始的。
也就是说，我们这一轮跳fail是从刚刚匹配到的 \(\texttt{aa}\) 的fail开始，也就是从 \(\texttt{a}\) 开始。

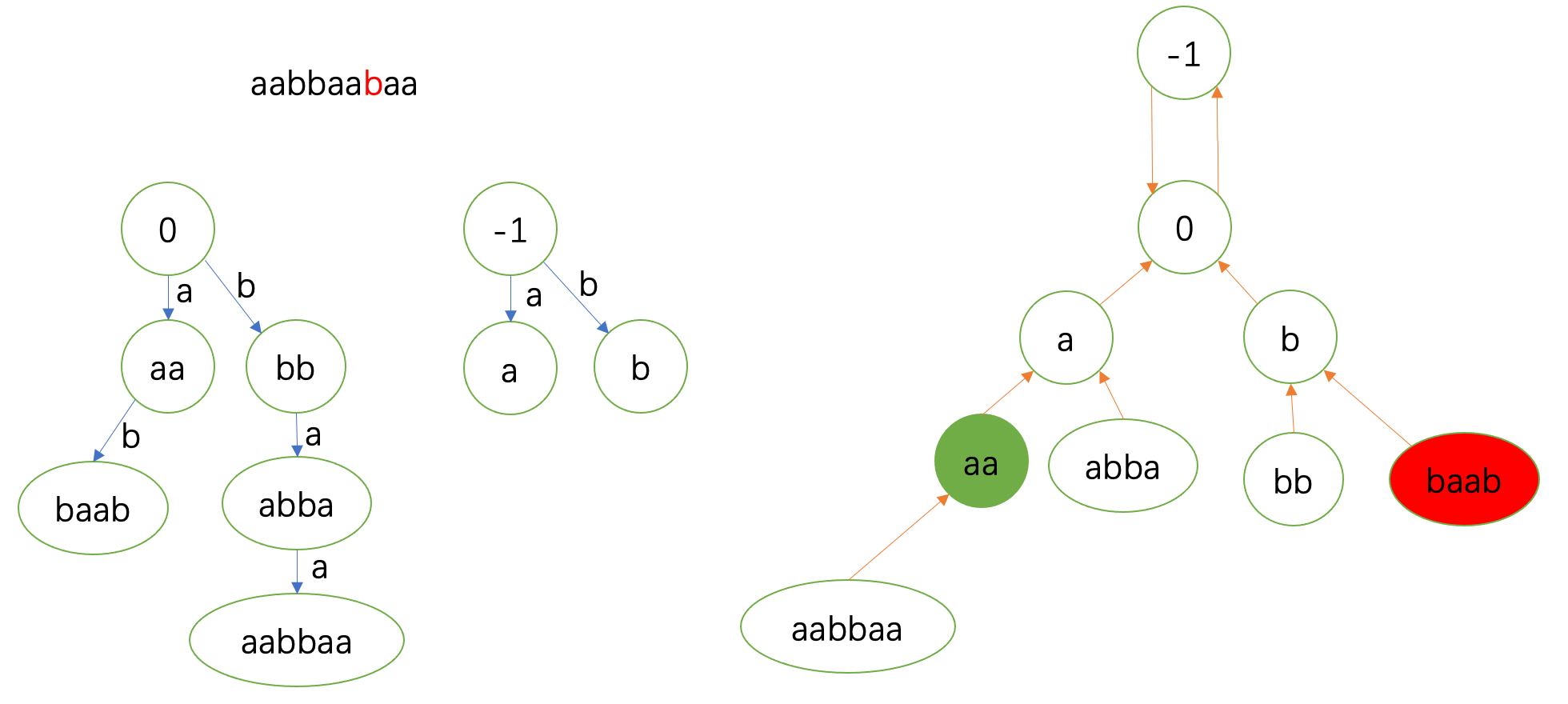
接下来的 \(\texttt{a}\) 在 \(\texttt{b}\) 处匹配。

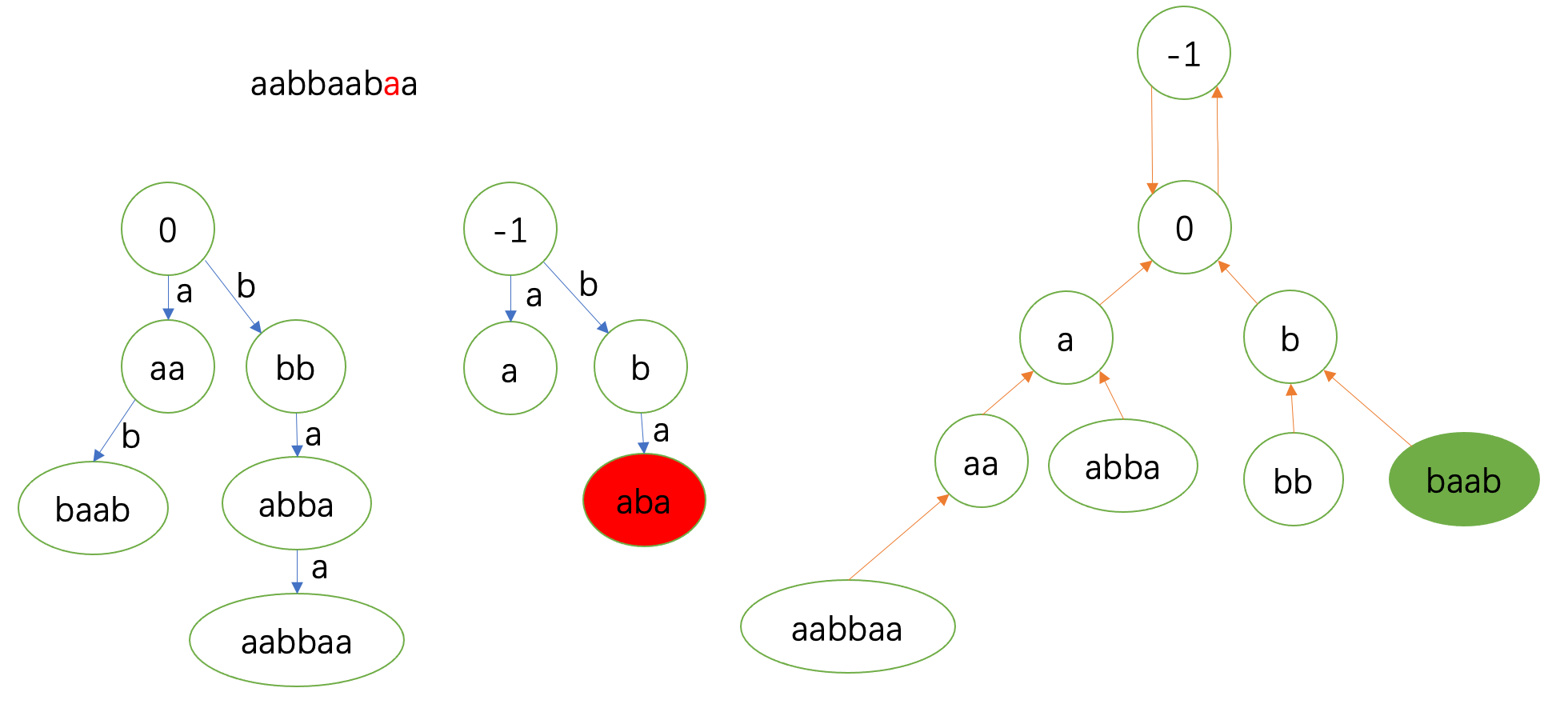
需要注意的和上面相同。这一轮跳fail是从 \(0\) 开始的，到 \(-1\) 匹配。

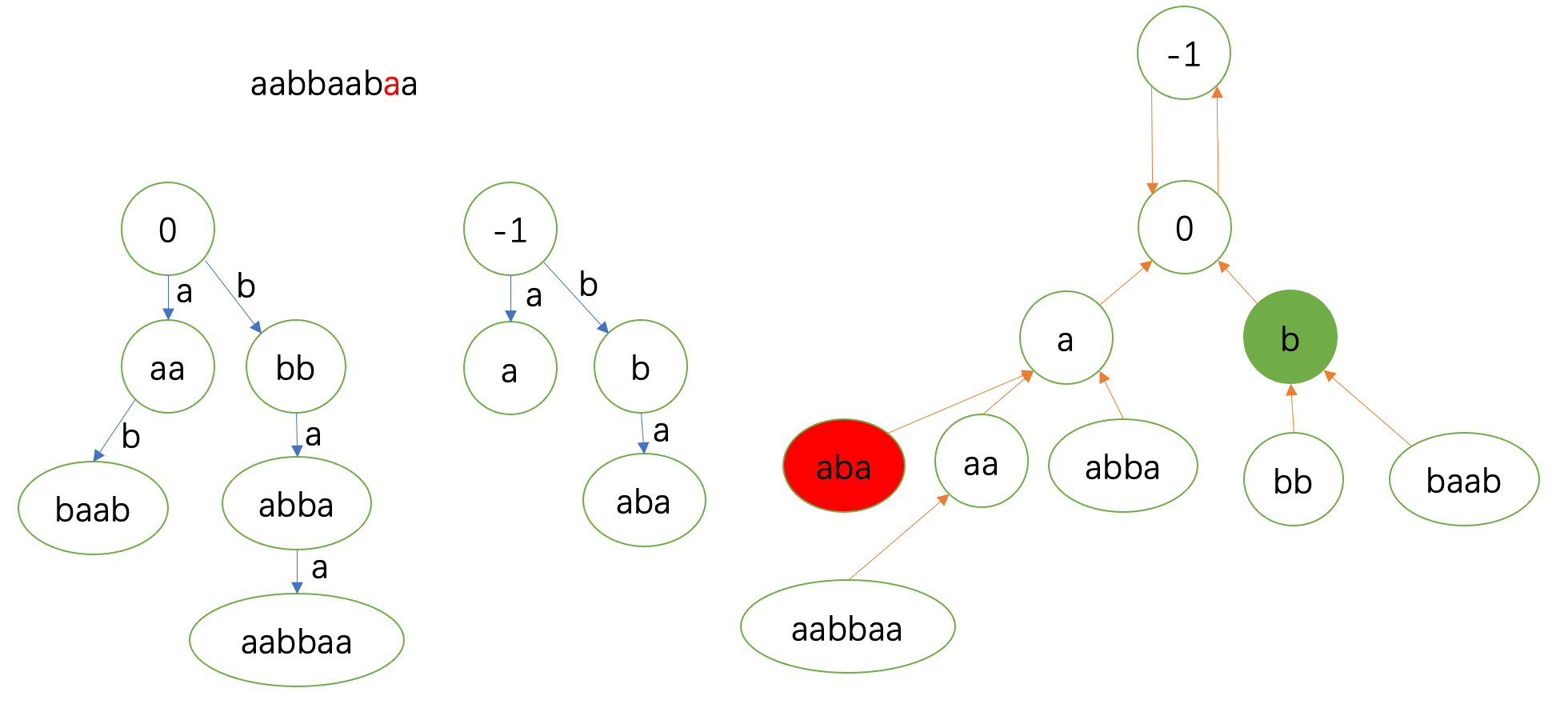
最后一个 \(\texttt{a}\)。

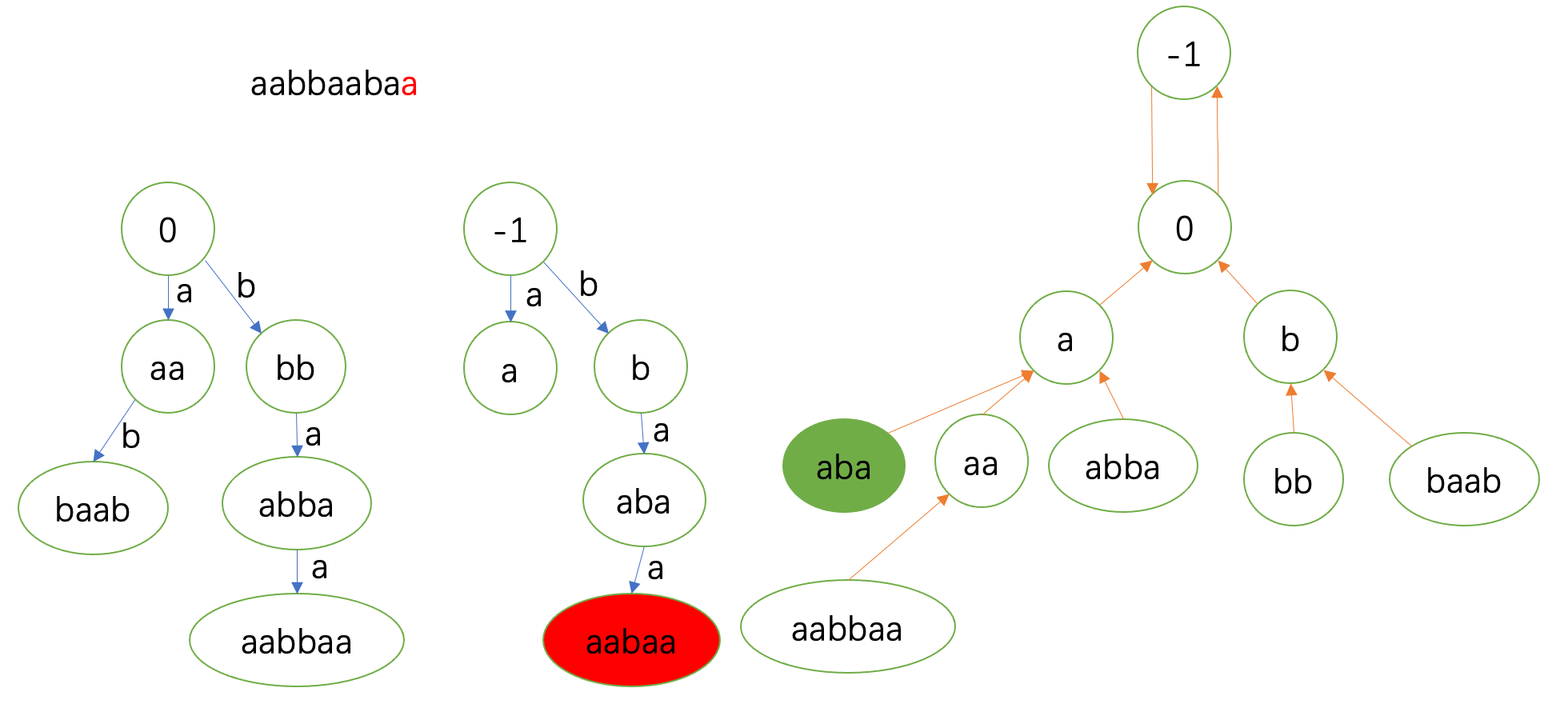
连fail边时在 \(0\) 处匹配。

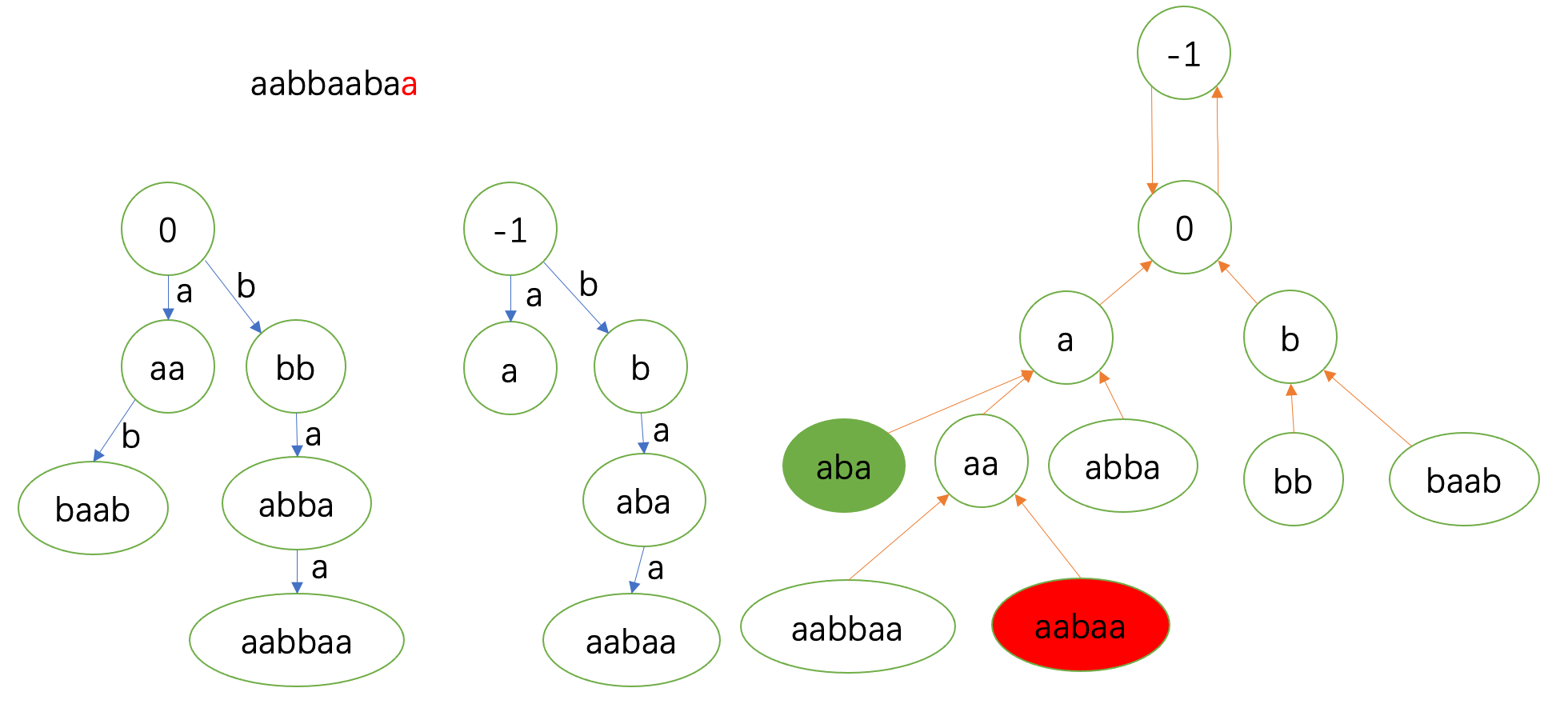
最后的结果：

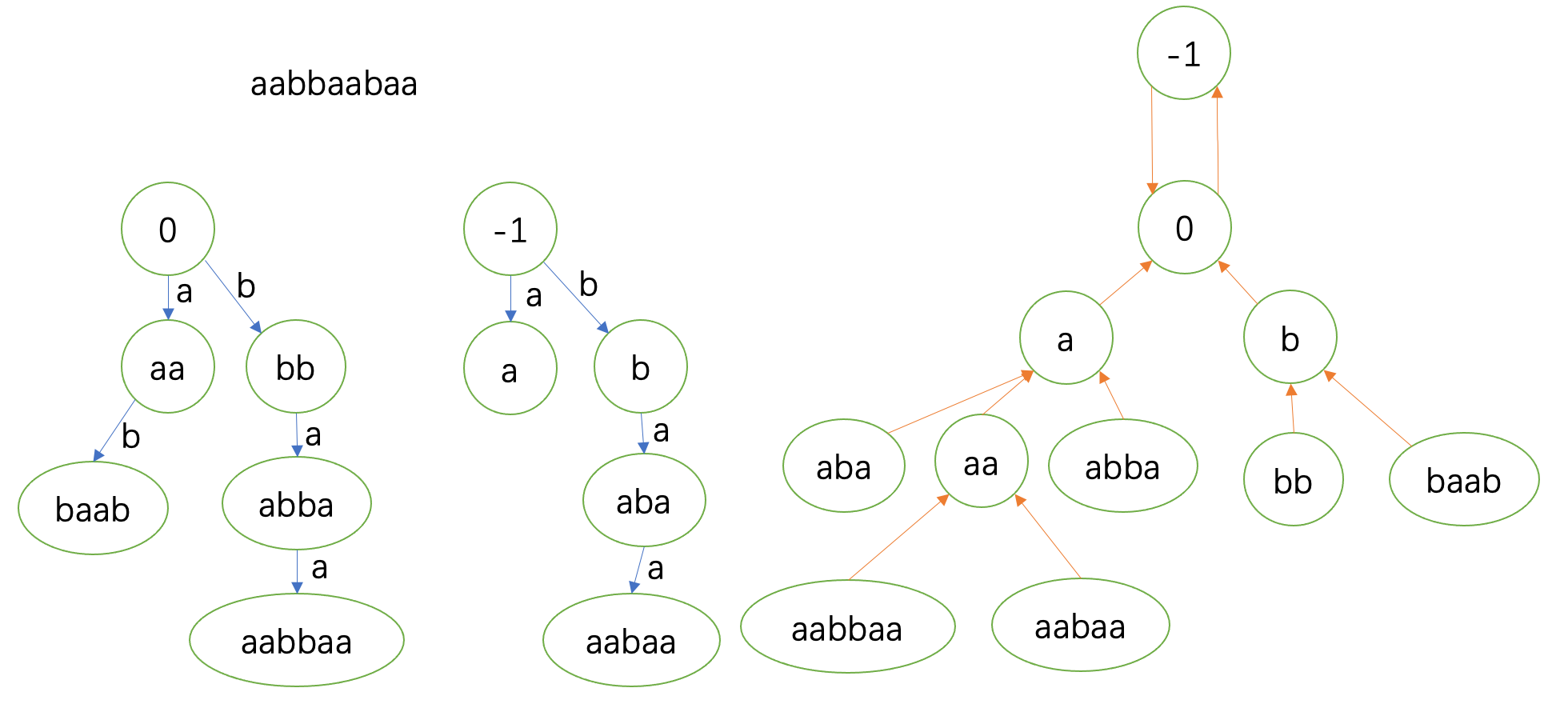
这就完成了对回文自动机的构建。