自动机初步
0. 约定
字符串的下标从 \(0\) 开始。\(|s|\) 表示字符串 \(s\) 的长度。
对于字符串 \(s\),记其每一个字符分别为 \(s_0, s_1, \cdots, s_{|s|-1}\)。
子串 \(s_l, s_{l+1}, \cdots, s_{r-1}, s_r\) 简记为 \(s[l:r]\)。特别地,若 \(l=0\),可记作 \(s[:r]\);若 \(r=|s|-1\),可记作 \(s[l:]\)。
对于字符串 \(a, b\),\(a+b\) 表示拼接操作,即将字符串 \(b\) 拼接到字符串 \(a\) 之后,构成新的字符串。
记构成的新字符串为 \(c\),则上述拼接操作记为 \(c\gets a+b\)。
其中符号 \(x\gets y\) 表示将 \(y\) 的值赋给 \(x\)。
不论是字符还是字符串,皆不加引号。
1. 自动机
首先,我们需要明确自动机的概念。一般来说,OI中我们会接触到的都是确定有限状态自动机(DFA)。
DFA可以看成一张有向图,图上的节点称为状态(\(Q\)),而从一个状态到另一个状态的有向边称为转移。转移方式由转移函数(\(\delta\))进行规定。
DFA有一个起始状态(\(start\))和若干个接受状态(\(F\))。当我们把规定字符集(\(\Sigma\))中字符组成的字符串输入该DFA时,DFA会从起始状态开始,依照转移函数,逐个字符进行转移。
若最终停在了接受状态,称该DFA接受该字符串;否则称该DFA不接受该字符串。
从这里可以看出,DFA就是用来识别字符串的。
接下来我们对转移函数进行形式化定义。转移函数的形式为 \(\delta(u,c)=v\)。其中 \(u,v\) 都是状态,而 \(c\) 代表字符串中的字符。
如果我们不能从 \(u\) 状态由字符 \(c\) 转移到任何一个状态,我们称 \(\delta(u,c)=\text{null}\)。\(\text{null}\) 不是接受状态,且不能转移到接受状态,只能转移到 \(\text{null}\)。
我们还可以扩展转移函数的定义,让其第二个参数称为字符串,此时转移函数的意义就为从 \(u\) 状态开始,依次按照字符串中字符进行转移,最终到达的状态。
形式化地,\(\delta(u,s)=\delta(\delta(u,s_0),s[1:])\)。
2. 一些简单的DFA
然而DFA理论并没有帮助我们解决问题。
因此这里我们讨论一些实际应用中简单的DFA。
2.1. Trie树
Trie树就是最简单的DFA。
初始状态就是Trie树的根,转移就是Trie树中的边,而接受状态就是你把字符串存进去后打了标记的点。
Trie树的作用就是识别字符串是否在字典中。
2.2. KMP自动机
KMP算法也可以视作一个自动机。
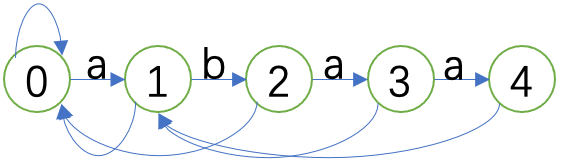
如图,我们对字符串 \(\texttt{abaa}\) 建立了一个自动机,其中 \(0\) 是起始状态,最后的 \(4\) 是接受状态。
可以看出,整个自动机的结构分为两部分,一部分是上面的链,另一部分是下面的失配指针。失配指针就是由 \(i\) 指向 \(\pi(i-1)\) 的指针。
形式化地,转移函数定义为:
\(\delta(i,c)=\begin{cases}0&s_0\ne c\land i=0\\i+1&s_i=c\\ \delta(\pi(i-1),c)&s_i\ne c\land i>0\end{cases}\)
可以自己尝试举例,如 \(\texttt{aaabaaabaa}\),这个自动机应当给出 \(\texttt{abaa}\) 在其中的全部出现。
2.3. 子序列自动机
顾名思义,子序列自动机就是识别字符串子序列的自动机。
也就是说,这个自动机要能够表示原字符串所有的子序列。
一个显然的构造方法是令 \(\delta(u,c)\) 为字符 \(c\) 在 \(u\) 之后第一次出现的位置。
如下图,我们对 \(\texttt{abcba}\) 建立子序列自动机:
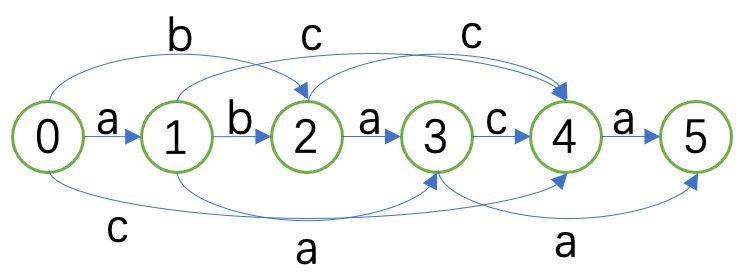
意义如上。可以看出这就包含了原字符串所有的子序列。另外需要注意的是,图中的 \(0\) 为起始状态,而任意一个节点都可以是接受状态。
一个简单的构造方法是,从后往前扫,记录每个字符当前最靠前的出现位置就可以了。
不幸的是,对于这道模板题,我们并不能直接按照上述方式进行构建。
因为按照上述方式进行构建的时间复杂度高达 \(O(n|\Sigma|)\),再加上自动机识别的 \(O(\Sigma L)\),显然不能通过本题。
事实上一般情况下这样已经够用了,因为 \(|\Sigma|\) 通常不会太大。
我们还是需要挖掘 \(\delta\) 的性质。通过观察我们可以发现,相邻两个状态的转移函数对于相同的字符集,每次只会有一个值发生变化。
对于上面的例子,我们把 \(\delta(i,\texttt{a}),\ \delta(i,\texttt{b}),\ \delta(i,\texttt{c})\) 用三元组表示:
\((1,2,4)\leftarrow(3,2,4)\leftarrow(3,-1,4)\leftarrow(5,-1,4)\leftarrow(5,-1,-1)\leftarrow(-1,-1,-1)\)
并且发生修改的数值也很容易确定,就是字符 \(s_i\) 对应的值被修改为了 \(i+1\) 而已。
建立自动机时修改创建新版本,每次自动机进行识别的时候需要访问历史版本;
我们自然想到可以使用可持久化线段树来进行优化。时间复杂度 \(O((n+\Sigma L)\log|\Sigma|)\)。
code:
const int maxn=100010;
int type,n,q,m,cnt,rt[maxn],a[maxn],s[maxn];
struct node{int l,r,val;}tree[maxn*20];
void build(int &x,int l,int r)
{
x=++cnt;
if(l==r){tree[x].val=a[l];return;}
int mid=(l+r)>>1;
build(tree[x].l,l,mid);
build(tree[x].r,mid+1,r);
}
void modify(int &k,int ver,int x,int l,int r,int val)
{
k=++cnt;tree[k]=tree[ver];
if(l==r){tree[k].val=val;return;}
int mid=(l+r)>>1;
if(x<=mid)modify(tree[k].l,tree[ver].l,x,l,mid,val);
else modify(tree[k].r,tree[ver].r,x,mid+1,r,val);
}
int query(int k,int x,int l,int r)
{
if(l==r)return tree[k].val;
int mid=(l+r)>>1;
if(x<=mid)return query(tree[k].l,x,l,mid);
else return query(tree[k].r,x,mid+1,r);
}
//----------以上为可持久化线段树板子----------
//main函数内
for(int i=0;i<n;i++)s[i]=read();//从0开始读入是字符串的习惯
memset(a,-1,sizeof(a));//初始时要赋成-1
build(rt[n],1,m);//m是字符集大小
for(int i=n-1;i>=0;i--)modify(rt[i],rt[i+1],s[i],1,m,i+1);//建立子序列自动机
for(int i=1;i<=q;i++)
{
int l=read(),c,p,now=0,flag=1;
for(int j=0;j<l;j++)
{
c=read();
if(!flag)continue;
p=query(rt[now],c,1,m);//p为指针
if(p==-1){flag=0;continue;}//如果失配说明一定不是子序列;但是我们还是把剩下的读完,所以不能退出循环。
now=p;//转移
}
if(!flag)printf("No\n");
else printf("Yes\n");
}


