单调队列与单调栈
感觉自己对这种数据结构理解的一直不是很好……
于是就有了这一篇。相信所有人都能看懂（
符号约定：
- 对于队列，使用[表示队首，使用]表示队尾。
- 对于栈，使用<表示栈顶，使用]表示栈底。
1. 单调队列
1.1 什么是单调队列
顾名思义，“单调队列”就是队列内元素满足单调性的队列。
比如下面这三个队列：
[3 6 9 10] [90 4 2 -1] [6 4 2 5]
显然前两个队列满足单调性，而最后一个不满足。不妨称第一个队列为单调递增的，而第二个为单调递减的。
1.2 如何满足队列的单调性
这个非常简单。比如说我们遇到了一个单调递增的队列：
[1 4 6]
但是这个时候我们要插入2。于是为了满足队列的单调性，我们将4和6从队尾移除，并从队尾插入2。
最后队列就变成了：
[1 2]
有一句著名的话就体现了单调队列的性质（当然此处说的应是单调递减的单调队列）：
如果一个人比你小，又比你强，那你就打不过他了。
但是这里有两个需要注意的点。
- 这个队列是可以从队尾移除元素的，所以这并不是一个我们一般所说的队列。
方便起见，我们会使用STL中的deque来模拟单调队列。 - 为什么不把4和6再push回去？
这保证了单调队列的时间复杂度。
如果像刚刚这样做，那么对于一个单调递增的队列，插入倒序的数列时间复杂度直接\(O(n^2)\)。如：
1000000 999999 999998 ...... 2 1
但是，如果我们将元素pop出之后就不再将其push进队列，
那么容易发现每个元素最多进队一次，出队一次，
如此时间复杂度达到了优秀的\(O(n)\)。
1.3 单调队列的应用两例
单调队列中的元素都是具有单调性的，于是我们用单调队列来维护具有单调性的数据（废话
1.3.1 维护定长区间最值
题意：
有一个长为 \(n\) 的序列 \(a\)，以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。
这里只分析最大值，最小值同理可得。
注意到，答案所对应的数组下标是满足单调递增的。
举个具体的例子（取\(k=3\)）：
i 1 2 3 4 5 6 7 8
a[i] 1 9 2 6 0 8 1 7
写下对应的答案所对应的数组下标：（遇到重复的\(a[i]\)时，令答案为下标大的）
ans 2 2 4 6 6 6
的确是单调递增（当然并不严格递增）的。
为什么呢？
直接凭直觉是显然的，毕竟如果出现一个答案更早的，那它也应该出现在ans数组的更早位置上。
这样，我们就可以考虑构造一个存储数组下标的单调队列。每次从队头取答案。
我们从1开始，依次插入数组下标。对应地，窗口也进行滑动。
将要插入的数字位于插入滑动窗口移动后的最右端。
如果此时队头超出了窗口范围，那么就将其弹出。
如果此时将要插入的数字比队尾大，那就弹出队尾，直到队尾大于要插入的数或队列为空。
（因为此时滑动窗口已经滑到了这个将要插入的数字，前面的数字已经不可能再为答案了）
文字描述过于抽象？实际模拟一遍。还是用之前的例子。
这次ans数组就直接表示答案而不是下标了，最后一行代表单调队列，\(k=3\)。
i 1 2 3 4 5 6 7 8
a[i] [1] 9 2 6 0 8 1 7
ans
[1]
i 1 2 3 4 5 6 7 8
a[i] [1 9] 2 6 0 8 1 7
ans
[2] //a[2]>a[1]，将1弹出
i 1 2 3 4 5 6 7 8
a[i] [1 9 2] 6 0 8 1 7//滑动窗口初始化完成，接下来向右移动
ans 9
[2 3]
i 1 2 3 4 5 6 7 8
a[i] 1 [9 2 6] 0 8 1 7
ans 9 9
[2 4]//a[4]>a[3]，将3弹出
i 1 2 3 4 5 6 7 8
a[i] 1 9 [2 6 0] 8 1 7
ans 9 9 6
[4 5]//2超出范围被弹出
i 1 2 3 4 5 6 7 8
a[i] 1 9 2 [6 0 8] 1 7
ans 9 9 6 8
[6]//a[6]>a[5]，a[6]>a[4]故4、5被弹出
i 1 2 3 4 5 6 7 8
a[i] 1 9 2 6 [0 8 1] 7
ans 9 9 6 8 8
[6 7]
i 1 2 3 4 5 6 7 8
a[i] 1 9 2 6 0 [8 1 7]
ans 9 9 6 8 8 8
[6 7 8]
非常完美。那接下来就是最大值的(部分)代码：
const int maxn=1000010;
int n,k,cnt,a[maxn],maxans[maxn];
deque<int> maxint;//用deque模拟单调队列
void push(int pos)
{
//访问front和back之前先判空是个好习惯
while(!maxint.empty()&&maxint.front()<=pos-k)maxint.pop_front();//将超出窗口范围的弹出(其实最多只弹一次，不用写while循环)
while(!maxint.empty()&&a[maxint.back()]<=a[pos])maxint.pop_back();//将队尾小于要插入的数的都弹出
maxint.push_back(pos);
}
int main()
{
//......
for(int i=1;i<k;i++)push(i);//前(k-1)个不取答案
for(int i=k;i<=n;i++)
{
push(i);
maxans[k]=a[maxint.front()];
}
}
1.3.2 单调队列优化dp
以luoguP2627 Mowing the Lawn为例。
首先写出状态转移方程。
令\(dp_i\)表示第\(i\)头奶牛能得到的最大效率。
有\(dp_i=\max\{dp_{j-1}+\sum\limits_{k=j+1}^{i}E_k\},\ i-K\leqslant j\leqslant i\)
预处理前缀和进行优化。令\(S_i=\sum\limits_{k=1}^iE_k\)，
则原dp方程可以化为：
\(dp_i=\max\{dp_{j-1}-S_j\}+S_i,\ i-K\leqslant j\leqslant i\)
那接下来应该怎么办呢……
考虑之前的滑动窗口问题。我们不妨也将要求的写成dp方程的形式。
令\(dp_i\)表示滑动窗口以\(a[i]\)为结尾取得的最大值。
\(dp_i=\max\{a[j]\}\ ,i-k+1\leqslant j\leqslant i\)
可以说是几乎完全一致了。
原题目中dp方程最后的\(S_i\)没有什么影响，单调队列优化的是取\(\max\)；
\(\max\)里的\(dp_{j-1}\)也没有影响，因为我们是顺推，\(dp_{j-1}\)已经算完了。
这样原题目就可以看成是一个大小为\(K+1\)的窗口依次向右滑了。
于是只要简单对应一下就行了ヽ(°▽°)ノ
附完整代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <deque>
#define int long long//不开long long见祖宗
using namespace std;
int n,k,sum[100010],dp[100010];
deque<int> q;
inline int posval(int pos){return dp[pos-1]-sum[pos];}
void push(int pos)
{
while(!q.empty()&&q.front()<pos-k)q.pop_front();
while(!q.empty()&&posval(q.back())<=posval(pos))q.pop_back();
q.push_back(pos);
}
signed main()
{
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++)
{
int xx;scanf("%lld",&xx);
sum[i]=sum[i-1]+xx;
}
for(int i=1;i<=k;i++)
{
push(i);
dp[i]=sum[i];
}
for(int i=k+1;i<=n;i++)
{
push(i);
dp[i]=posval(q.front())+sum[i];
}
printf("%lld\n",dp[n]);
return 0;
}
当然这道题算是单调队列优化dp模板中的模板，所以说思考起来比较简单。
再难了我也不会了qaq
2. 单调栈
2.1 单调栈的认识
单调栈与单调队列十分类似，就是栈内元素满足单调性的栈。
相比于单调队列，单调栈的应用没有那么广泛。
对于以下两个单调栈：
<1 5 10 11] <60 23 4 2]
称前一个是单调递增栈，后一个是单调递减栈。
要满足栈的单调性也很简单。只要在插入的时候，将不满足单调性的元素都弹出就可以了。
举个例子，对于以下的单调递增栈：
<1 5 6]
此时要将元素4压入栈。
<4 5 6]
原来的1被弹出了。
同样地，因为每个元素最多入栈一次、出栈一次，因此总的时间复杂度为\(O(n)\)。
2.2 单调栈的应用
2.2.1 基础应用：求第一个比\(a_i\)大的元素
luoguP5788
题意：对于数组中每一个元素，求第一个大于它的元素的下标。不存在则答案为0。
算法：
构造一个单调递增栈。因为要求的是下标，所以从后往前依次插入元素的下标。每次当该可以合法插入时栈顶即为答案。
同样地我们来模拟一下。不妨使用题目中的样例。
i 1 2 3 4 5
a[i] 1 4 2 3 5
ans 0//5插入时栈为空，故答案为0
<5]
i 1 2 3 4 5
a[i] 1 4 2 3 5
ans 5 0//4插入时栈顶为5，故答案为5
<4 5]
i 1 2 3 4 5
a[i] 1 4 2 3 5
ans 4 5 0//3插入时栈顶为4，故答案为4
<3 4 5]
i 1 2 3 4 5
a[i] 1 4 2 3 5
ans 5 4 5 0//2插入时栈顶为5，故答案为5
<2 5]//a[2]>a[3]，a[2]>a[4]，故将3、4出栈
i 1 2 3 4 5
a[i] 1 4 2 3 5
ans 2 5 4 5 0//1插入时栈顶为2，故答案为2
<1 2 5]
可以看出，单调栈算法的确帮助我们\(O(n)\)时间解决了该问题。
其实正确性也很显然。
假设将要插入的下标为\(i\)，目前(不合法的)栈顶为\(j\)，第一个合法栈顶为\(k\)。
首先\(a[k]\)一定是\(a[i]\)的第一个大于它的元素。
这个应该很好理解，毕竟是从后往前扫，所以离\(a[i]\)越近的就越靠近栈顶；
同时根据单调栈的入栈方法，一定有\(a[k]>a[i]\)。
而目前不合法的栈顶应被弹出也是显然的。
毕竟如果有一个数\(x<a[j]\)，那就必然有\(x<a[i]\)，因此这个\(j\)也就没有存在的必要了，之后的答案里一定不会再有它了。
根据这个原理，我们还可以\(O(n)\)对于每一个数求出第一个小于，向前第一个大于，向前第一个小于它的数。
最后是原题核心部分代码：
for(int i=n;i>=1;i--)
{
while(!st.empty()&&a[st.top()]<=a[i])st.pop();
if(!st.empty())ans[i]=st.top();
st.push(i);
}
2.2.2 进阶应用：柱状图中最大的矩形
单调栈也能用来优化dp。以LeetCode84为例。
LeetCode上的题确实简单，这种题就已经算是"困难"了
做这道题需要之前那道题的基础。(毕竟单调栈就是用来干这个的)
题面：
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
看上去好像要统计的矩形个数至少能有\(O(nh)\)的级别。
但是真的有必要统计那么多吗？
用\(f_i\)表示完全包含第\(i\)个柱能取到的最大面积。
则\(f_i\)的值就是以第\(i\)个柱为高度，左右能扩展出的最大的矩形。
显然最终的答案\(ans=\max\{f_i\},\ 1\leqslant i\leqslant n\)
具体实现方法：
记第\(i\)个柱的高度为\(h_i\)。
然后令\(l_i\)为向前第一个小于\(h_i\)的数的下标，不存在则设为\(-1\)；(这里赋\(-1\)和\(n\)是因为LeetCode上输入数据为vector，下标从\(0\)开始)
令\(r_i\)为向后第一个小于\(h_i\)的数的下标，不存在则设为\(n\)。
则\(f_i=(r_i-l_i-1)h_i\)。然后套用之前的模板就行了。
不够直观？我们用样例的图片来研究一下。
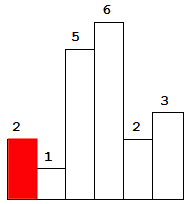
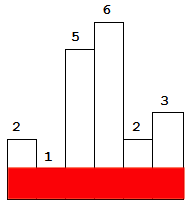
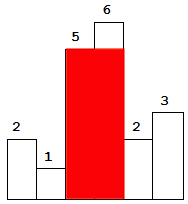
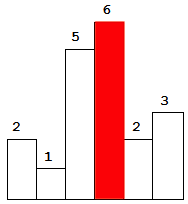
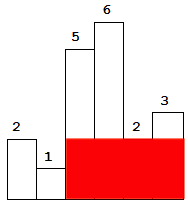
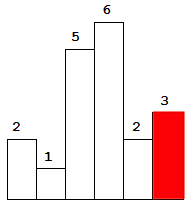
所以说其实我们只需要统计\(n\)个矩形。
最终代码：
stack<int> st;
int largestRectangleArea(vector<int>& heights)
{
int ans=0,n=heights.size();
vector<int> l,r;
for(int i=0;i<=n-1;i++)
{
l.push_back(-1);
r.push_back(n);
}
for(int i=0;i<=n-1;i++)
{
while(!st.empty()&&heights[st.top()]>=heights[i])st.pop();
if(!st.empty())l[i]=st.top();
st.push(i);
}
while(!st.empty())st.pop();
for(int i=n-1;i>=0;i--)
{
while(!st.empty()&&heights[st.top()]>=heights[i])st.pop();
if(!st.empty())r[i]=st.top();
st.push(i);
}
while(!st.empty())st.pop();
for(int i=0;i<=n-1;i++)ans=max(ans,(r[i]-l[i]-1)*heights[i]);
return ans;
}
