ST表与树状数组
一、ST表
最没用的一种，一般只用于静态区间RMQ（无修改，查询区间最大/最小值）。
(gcd 也能做, 只要能重复贡献就行 (也就是重复计算不会影响结果) )
但是ST表的查询操作复杂度异常优秀，能做到\(O(1)\)，这是其它数据结构难以做到的。
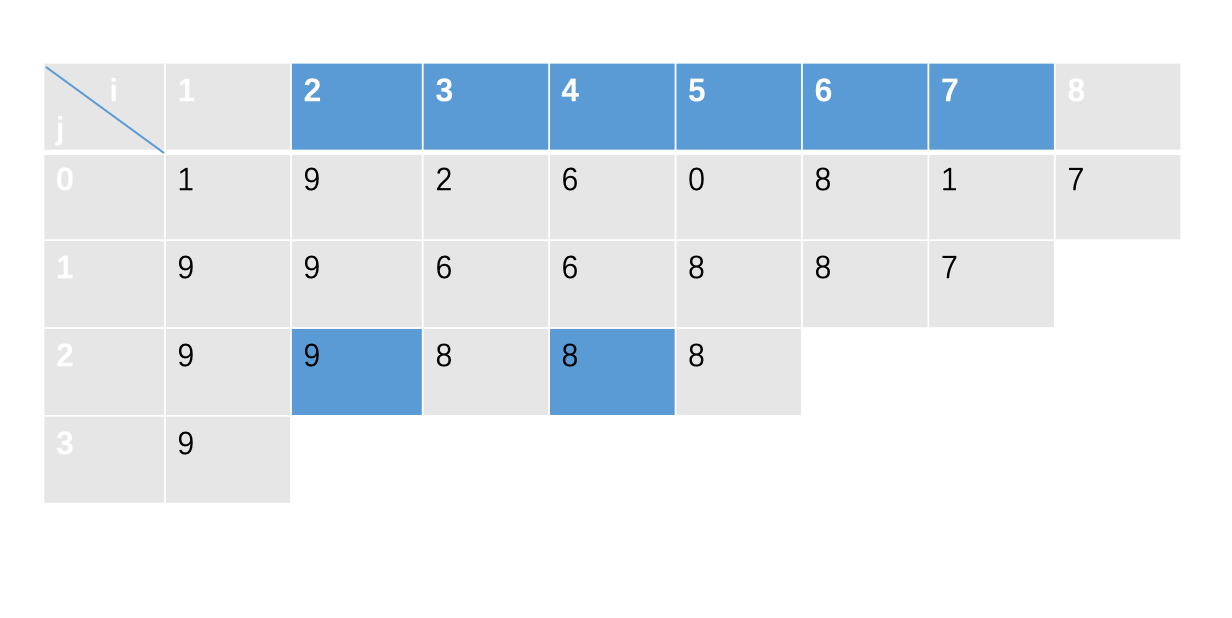
ST表的思路大致就是用一个二维数组\(f[i][j]\)来表示\(a[i], a[i+1], \cdots a[i+2^j-1]\)，也就是从\(i\)开始的长为\(2^j\)的序列的最大值。
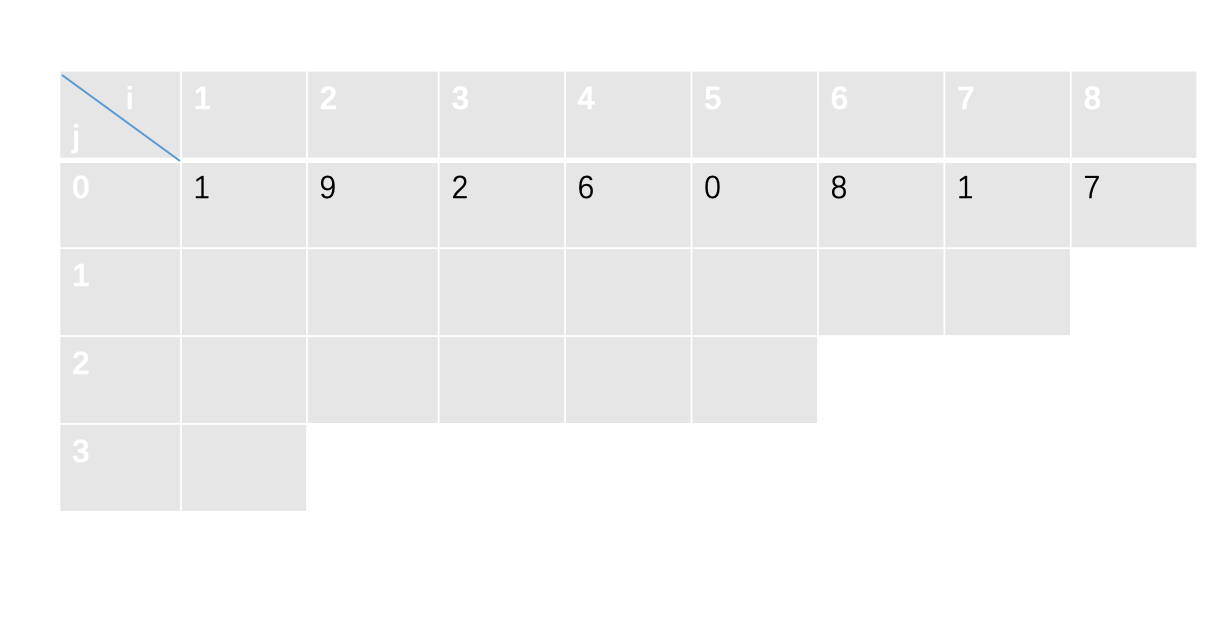
我们以一个长为8的数列作为例子：（取最大值）
首先我们将原数列的数字放到\(f[i][0]\)中：
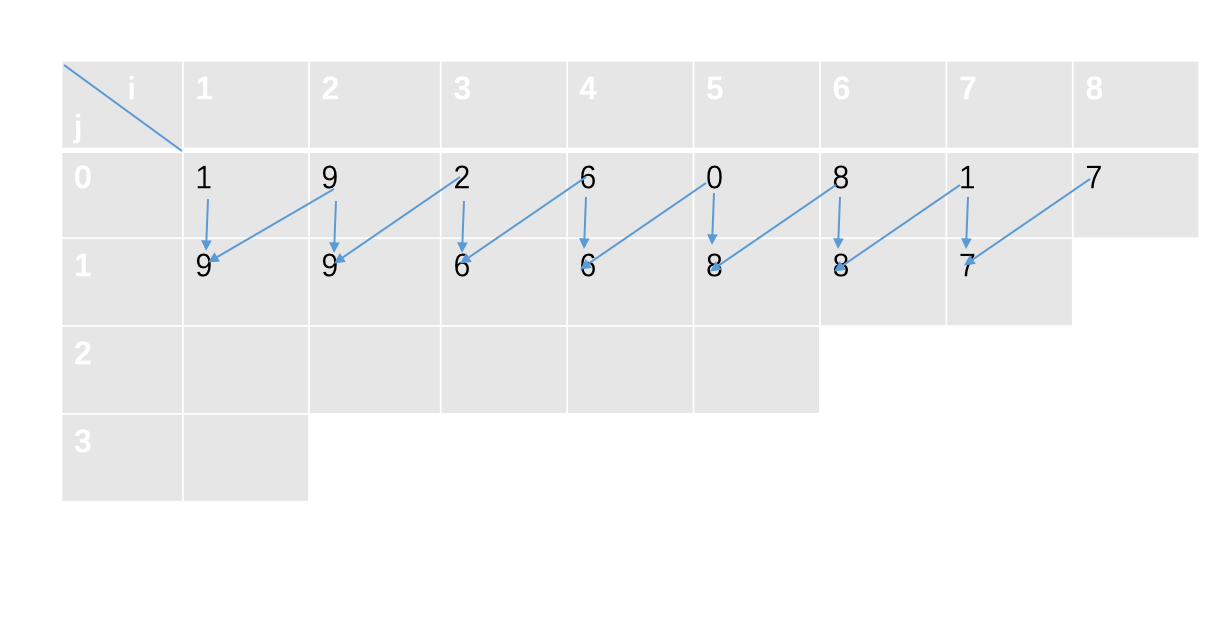
接下来开始刷表。
我们将现在需要处理的序列分成前后两半，这当中的每一半都已经处理完成了。
于是我们只需要调用对应这两半的两个值再取最大/最小就可以啦qwq
容易发现，对于\(f[i][j]\)来说对应的这两个值就是\(f[i][j-1]\)和\(f[i+2^{j-1}][j-1]\)。
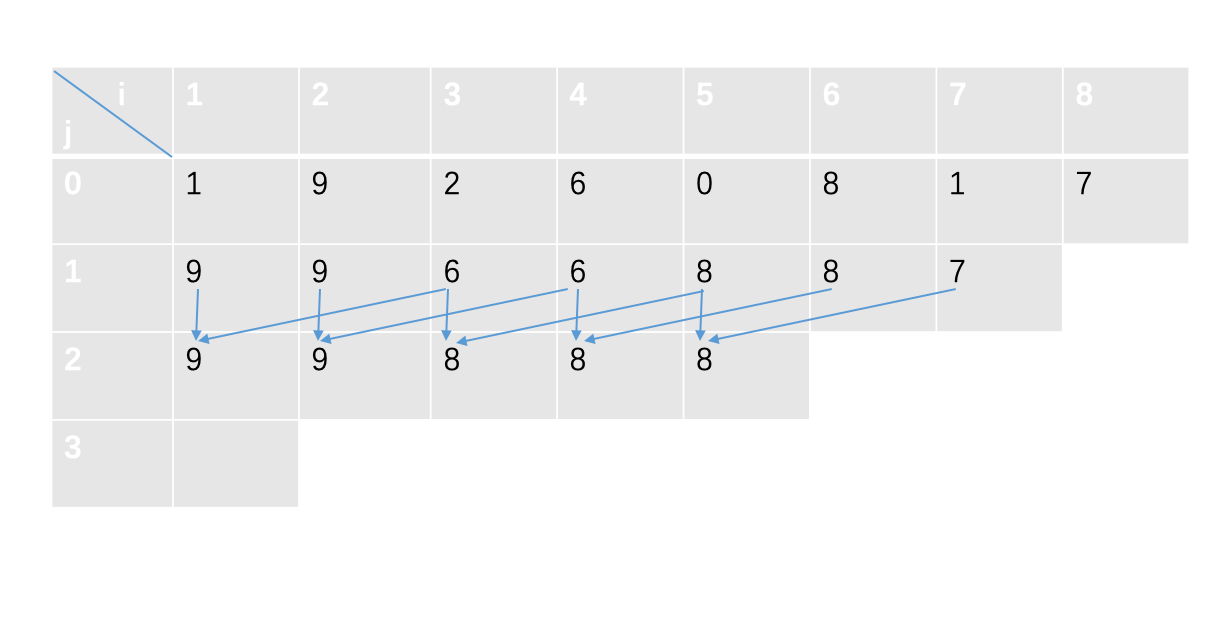
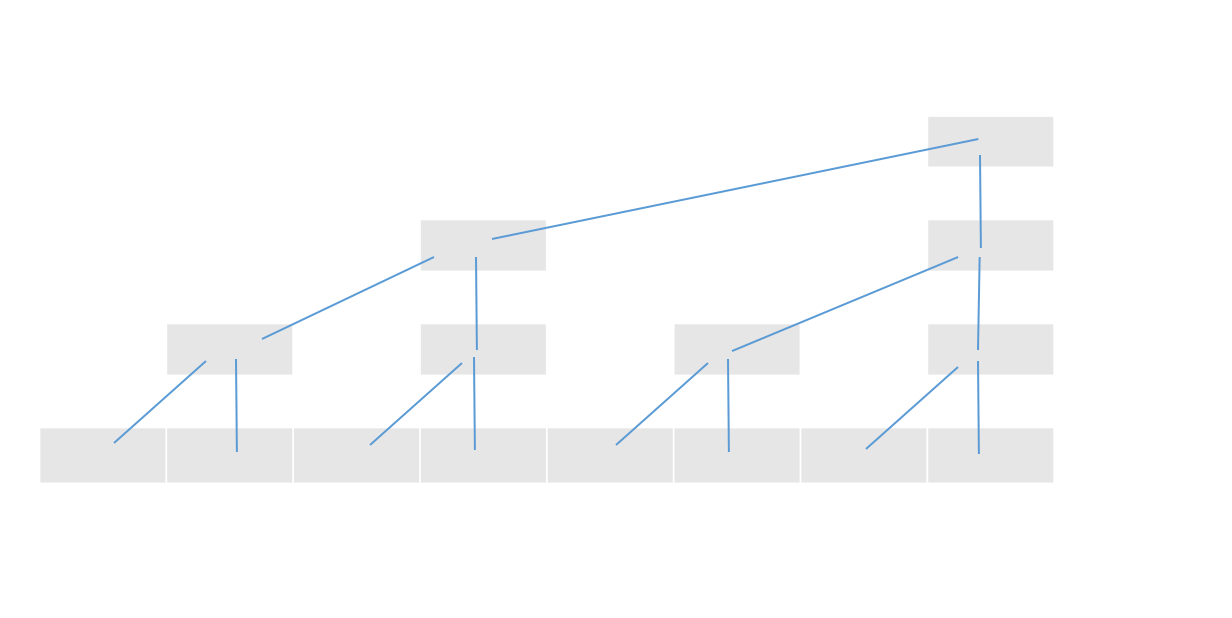
接下来就是刷表的图示，箭头表示是当前值是由哪两个值处理的。
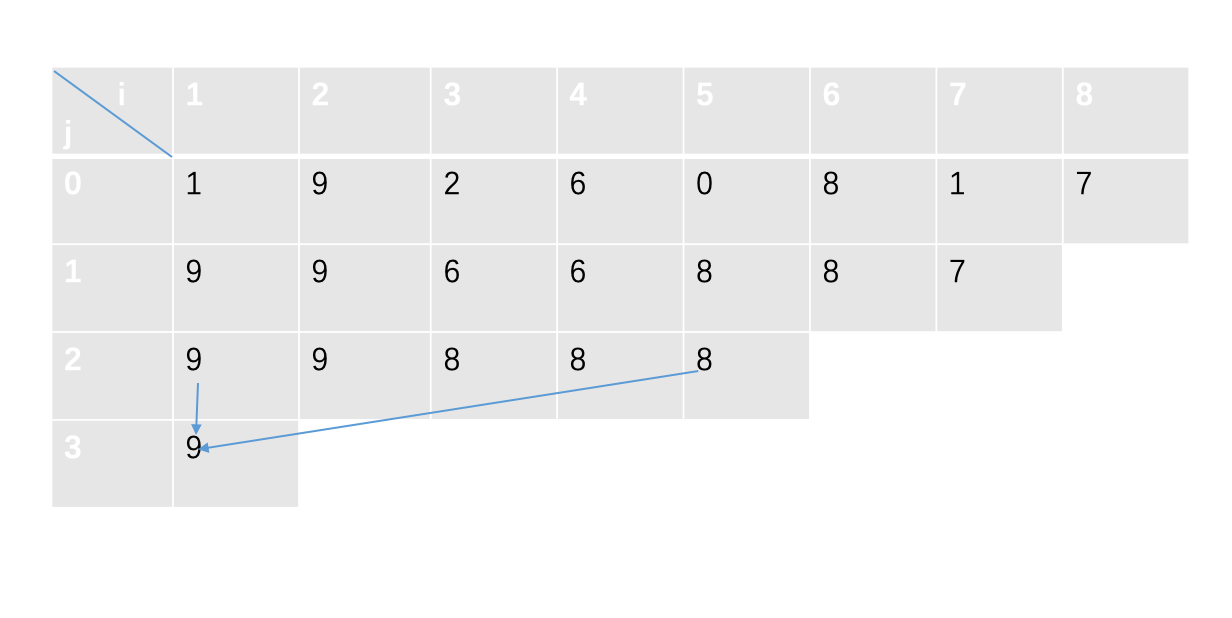
接下来是查询。
我们将需要查询的区间拆成已经有表示的前后两部分，再取最大值即可。
比如在刚刚的ST表中查询区间[2,7]:
只需拆成[2,5], [4,7]两个就行了。
我们记区间长度为\(k\)，则\([l,r]\)可拆成\(f[l][log_2k]\)和\(f[r-2^{log_2k}+1][log_2k]\)两个询问。（注意log要下取整）
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m,ans,l,r,k,lg2[100010],st[100010][20];
int main()
{
for(int i=2;i<100010;i++)lg2[i]=lg2[i/2]+1;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&st[i][0]);
for(int j=1;j<=lg2[n];j++)
for(int i=1;i+(1<<(j-1))<=n;i++)
st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&l,&r);
k=lg2[r-l+1];
ans=max(st[l][k],st[r-(1<<k)+1][k]);
printf("%d\n",ans);
}
return 0;
}
二、树状数组
我们来考虑这样一个问题：给定一个数组，每次有单点修改，区间查询和两种操作。
这时候因为有修改，前缀和不怎么管用了。当然，将区间[l,r]的和拆成[1,r]和[1,l-1]两个询问的思路还是很有用处的。
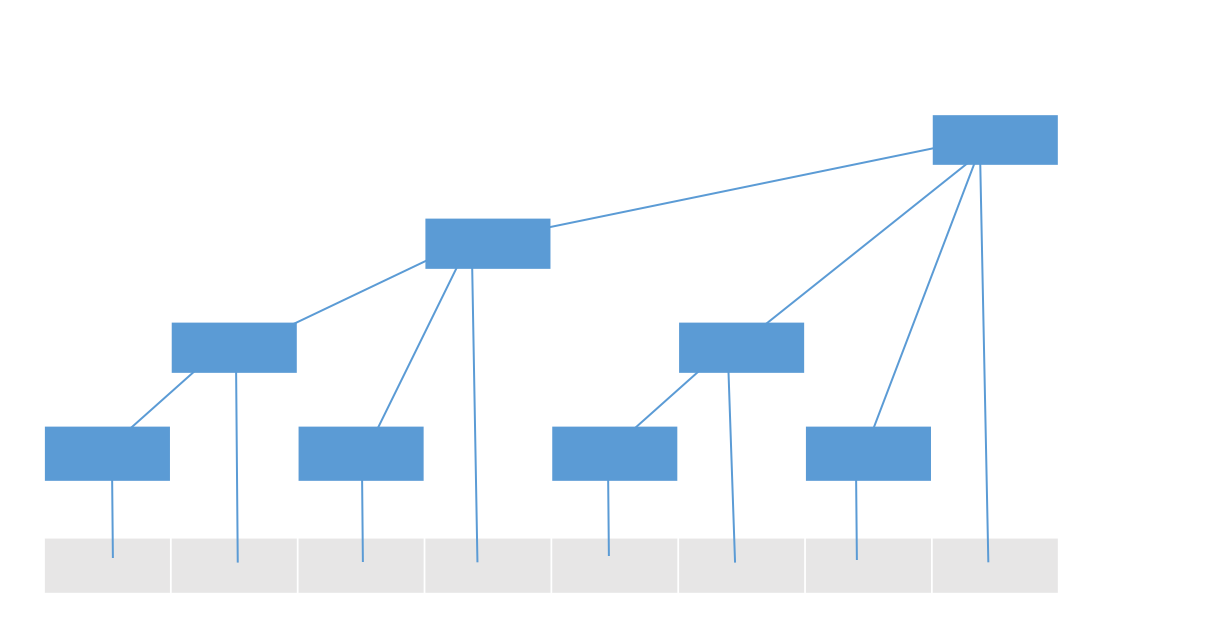
我们尝试来根据数组的节点建一棵二叉树来解决问题：（二叉树的每个节点表示他所对应的子树的和）
但这样就成一棵线段树了太麻烦了，我们尝试着将它简化一下。变成这个样子：
可以看到，我们将这棵二叉树拎了出来，并且让数组中的那个值对应它所能达到的最高的节点。节点意义同上。
但这个样子看上去就破坏了原有树的性质了。我们要从这棵奇怪的树里找出点规律来。
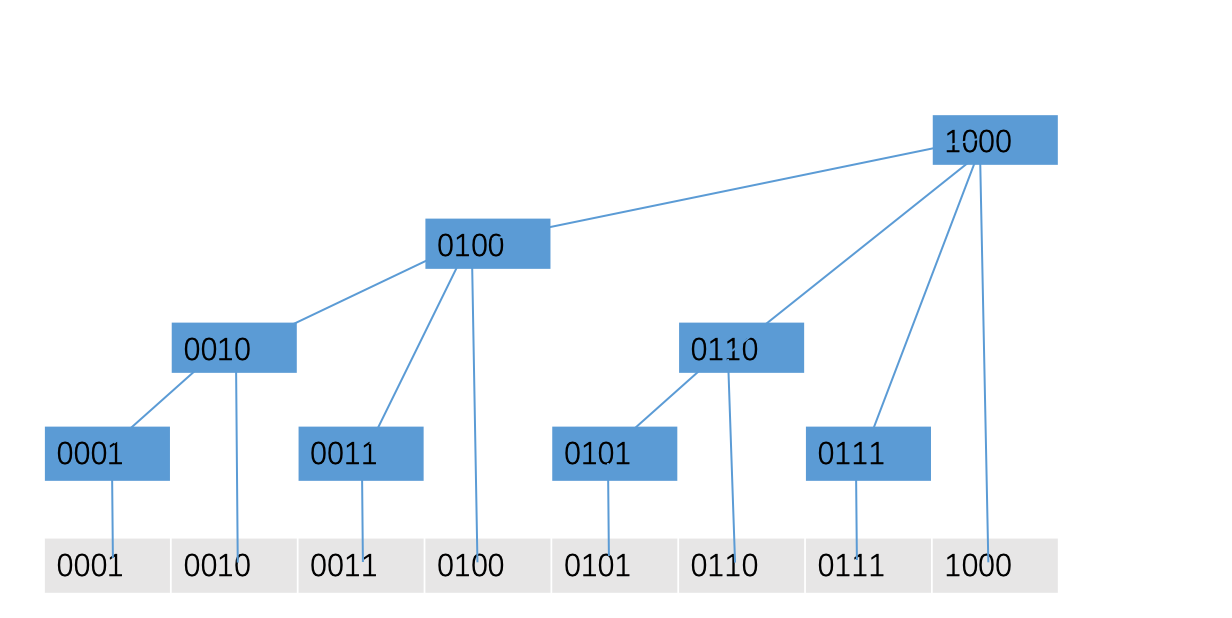
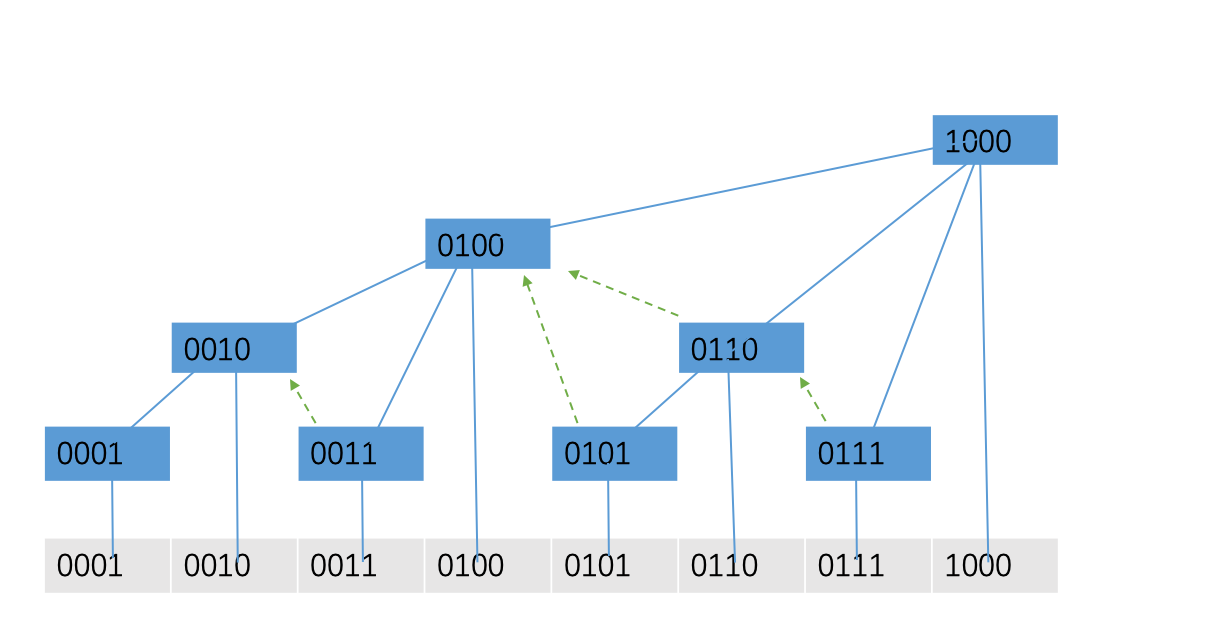
我们对树中的每个节点进行二进制标号：
可能还是比较抽象，我们可以定义一个函数lowbit(x)表示x的二进制表示中最低的1所对应的数。比如\((1110)_2\)的lowbit为\((10)_2\)。
当然这个函数可以简便地进行计算：
int lowbit(int x){return x&(-x);}
十分玄学。如果知道一点原反补码，模拟一下应该就能明白了（
那现在知道了这个函数，规律也很显然了：将下面的数加上这个数的lowbit，就得到了它的父亲的编号。
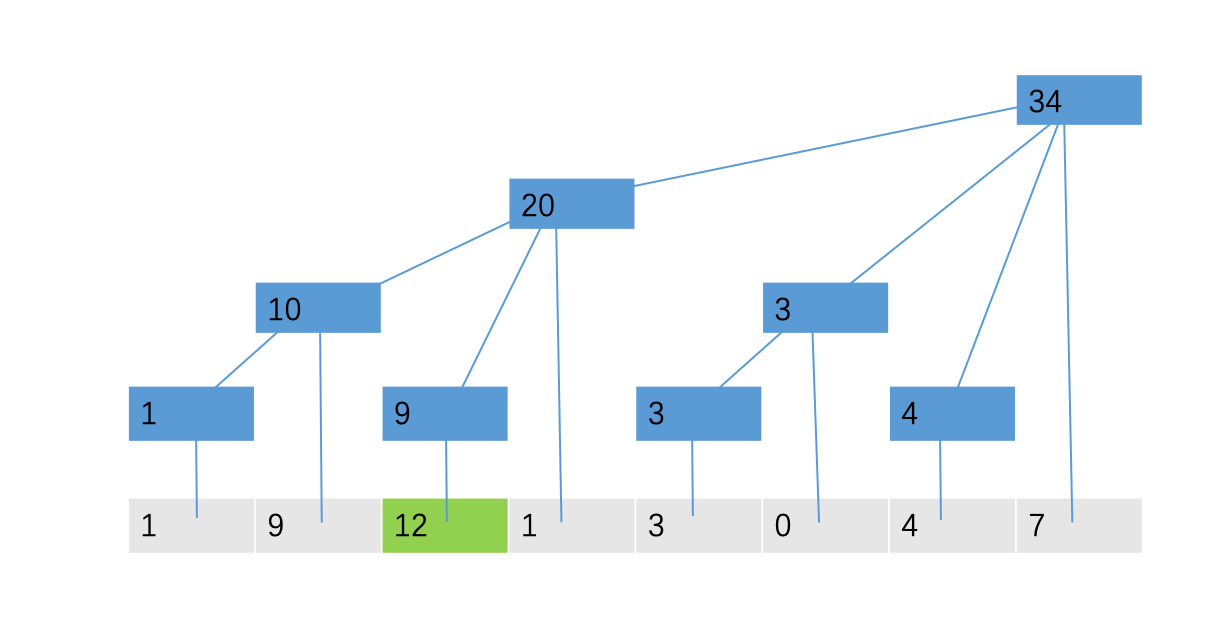
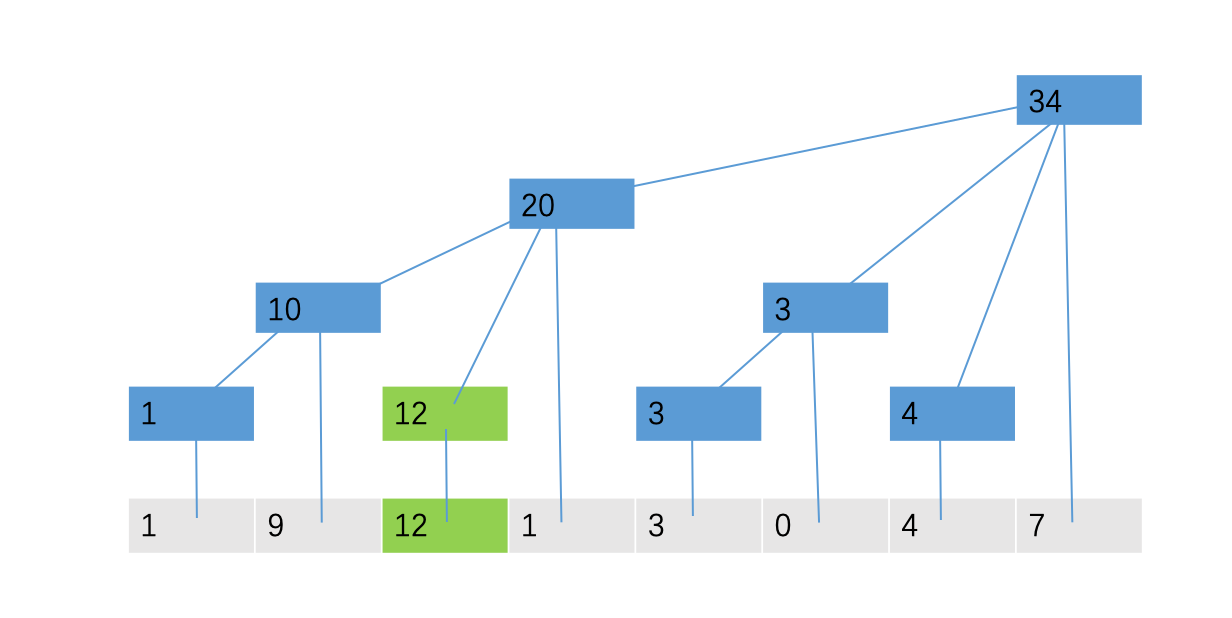
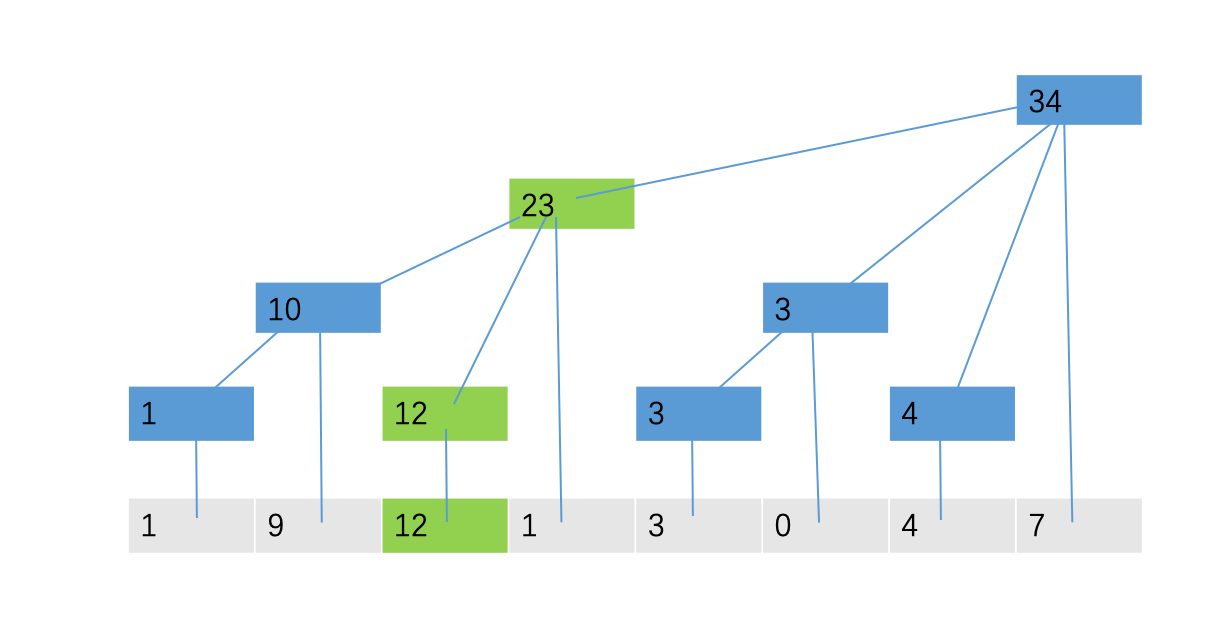
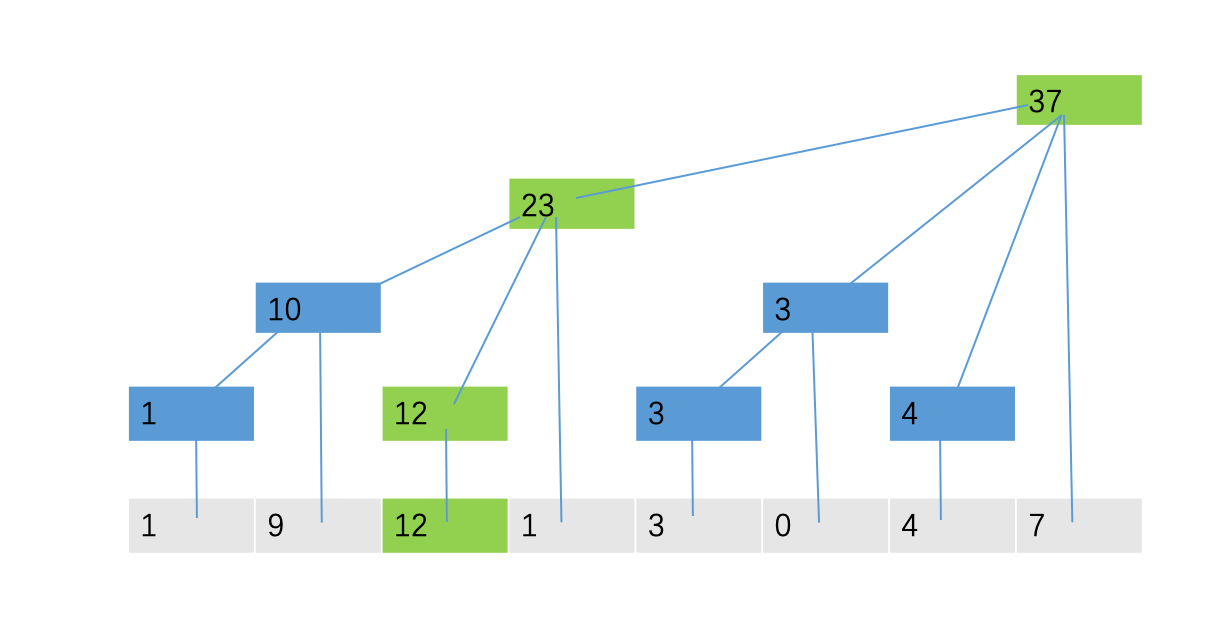
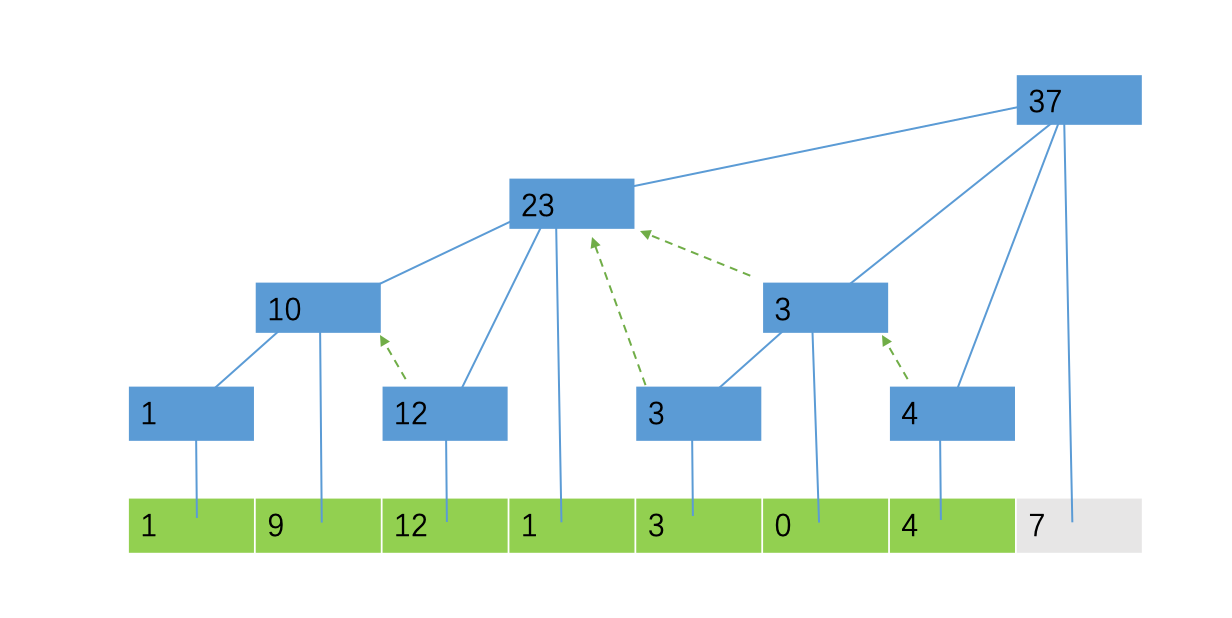
我们根据这个性质便可以进行单点修改的操作了。还是刚才的例子，我们尝试将第三个位置对应的9增加为12：
very simple.
实现代码：
void add(int x,int k){while(x<=n)a[x]+=k,x+=lowbit(x);}
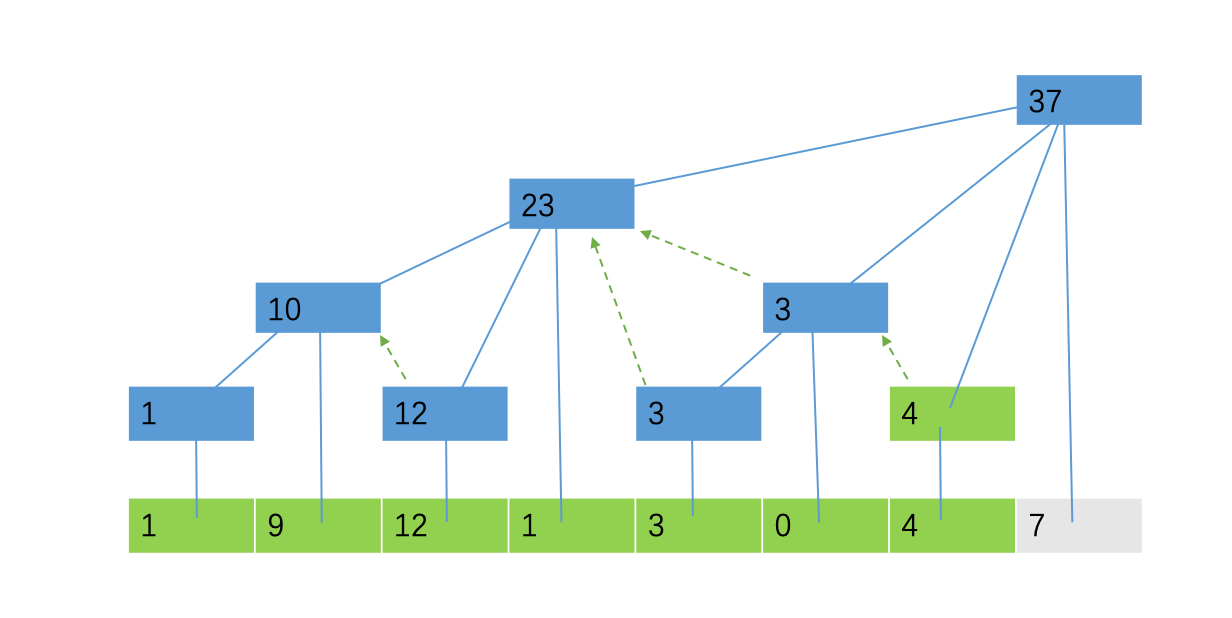
接下来是查询。由前面的思路，我们只需查从1开始的区间和即可。
在做这个操作之前，我们先引入树状数组的另一性质。
之前的规律是不停地加lowbit，那不停地减去lowbit会发生什么呢？
我们得到了这样一张图：
绿色虚线箭头表示减去lowbit的情况。
可以看出，这个操作相当于是跳到了它左边的那个兄弟子树上。（实际上如果我们画出0000节点，那么这些绿色箭头将会形成另一个树状数组）
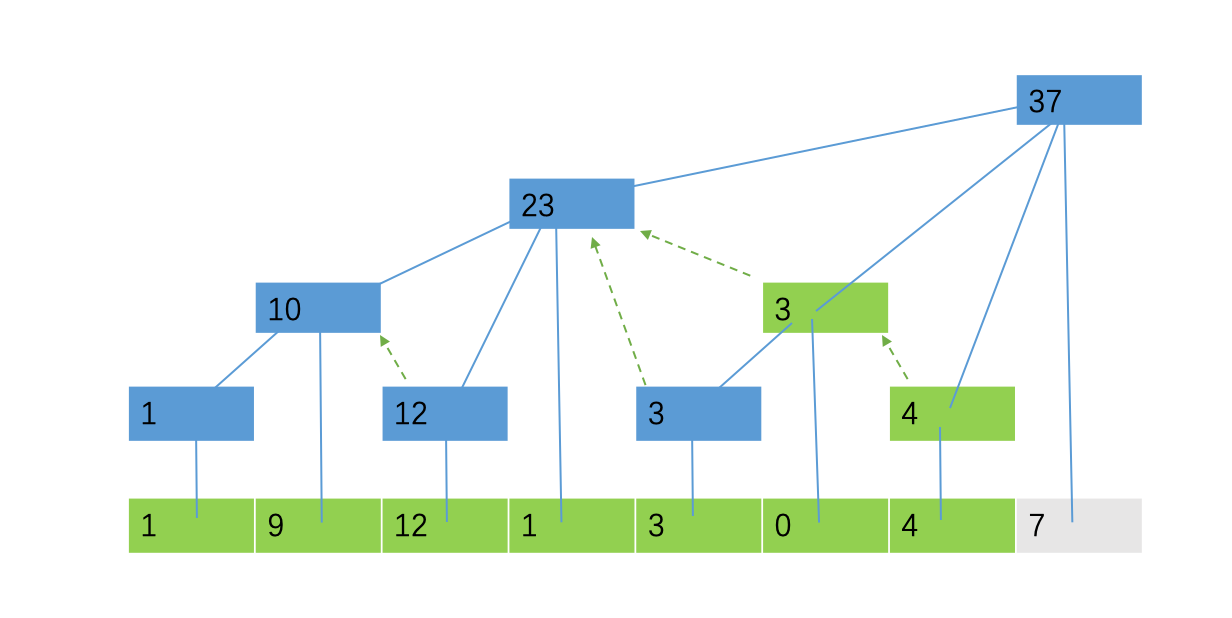
那么查询也显而易见了。不停地向左跳直到0即可。接下来是一个查询[1,7]的例子：
然后是查询的代码：
int query(int pos)
{
int ans=0;
while(pos)ans+=a[pos],pos-=lowbit(pos);
return ans;
}
0. 简单优化
(1)建树优化
普通的进行\(n\)次插入的方法会达到\(O(n\log n)\)，这种方法可以达到\(O(n)\)。
也可以认为，这是一种「部分插入」的方法。
for(int i=1;i<=n;i++)
{
int nxt=i+lowbit(i),xx;scanf("%d",&xx);
a[i]+=xx;if(nxt<=n)a[nxt]+=a[i];
}
(2)查询优化
就是分别跳l,r。（其实没什么用
inline int query(int l,int r)
{
int ans=0;l--;
while(r>l)ans+=a[r],r-=lowbit(r);
while(l>r)ans-=a[l],l-=lowbit(l);
return ans;
}
1. 单点修改区间查询
就是上面所说的。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m,a[500010];
inline int lowbit(int x){return x&(-x);}
inline void add(int x,int k){while(x<=n)a[x]+=k,x+=lowbit(x);}
/*
inline int query(int l,int r)
{
int ans=0;l--;
while(r>l)ans+=a[r],r-=lowbit(r);
while(l>r)ans-=a[l],l-=lowbit(l);
return ans;
}*/
inline int query(int pos)
{
int ans=0;
while(pos)ans+=a[pos],pos-=lowbit(pos);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int nxt=i+lowbit(i),xx;scanf("%d",&xx);
a[i]+=xx;if(nxt<=n)a[nxt]+=a[i];
}
for(int i=1;i<=m;i++)
{
int opt,x,y;
scanf("%d%d%d",&opt,&x,&y);
if(opt==1)add(x,y);
else printf("%d\n",query(y)-query(x-1));
}
return 0;
}
2. 区间修改单点查询
我们需要一点前置知识：差分
对于原数组\(a\)，我们定义它的差分数组为\(b\)，使得\(b_i=a_i-a_{i-1}\)。
由于我们默认\(a_0=0\)，于是有\(\sum\limits_{i=1}^{n}b_i=a_i\)。
运用差分有什么好处呢？我们可以将区间修改转化为单点修改，将单点查询变为区间查询。
具体地说，若我们要将\(a_l\)到\(a_r\)之间所有的元素（包括端点）都加\(k\)，我们只需要将\(b_l\)加上\(k\)，\(b_{r+1}\)减去\(k\)就行了。
于是我们成功将其转化为了所熟知的问题，写起来也非常简单了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m,a[500010],b[500010];
inline int lowbit(int x){return x&(-x);}
inline void add(int x,int k){while(x<=n)b[x]+=k,x+=lowbit(x);}
inline int query(int pos)
{
int ans=0;
while(pos)ans+=b[pos],pos-=lowbit(pos);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
int nxt=i+lowbit(i),xx=a[i]-a[i-1];
b[i]+=xx;if(nxt<=n)b[nxt]+=b[i];
}
for(int i=1;i<=m;i++)
{
int opt,x,y,k;
scanf("%d",&opt);
if(opt==1)
{
scanf("%d%d%d",&x,&y,&k);
add(x,k);add(y+1,-k);
}
else
{
scanf("%d",&x);
printf("%d\n",query(x));
}
}
return 0;
}
3. 区间修改区间查询
难度一下子上升了。不过我们还是可以试着用上一题的方法：差分。
这样子我们就解决了修改的问题。那查询呢？
我们试着推一下式子：
\(\begin{aligned}\sum\limits_{i=1}^ka_i&=\sum\limits_{j=1}^k\sum\limits_{i=1}^jb_i\\&=k\cdot\sum\limits_{i=1}^kb_i-\sum\limits_{j=1}^k(j-1)b_j\end{aligned}\)
我们可以用另一个树状数组\(c\)来维护\((j-1)b_j\)的值。
对\(c\)的修改只需要把\(c_l\)加上\((l-1)k\)，\(c_{r+1}\)减去\(rk\)即可。（思考一下为什么）
把上面的全部综合起来（别忘了开long long），就大功告成了！
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define int long long
using namespace std;
int n,m,a[100010];
class Bittree
{
public:
int num,datas[100010];
int lowbit(int x){return x&(-x);}
void add(int x,int k){while(x<=num)datas[x]+=k,x+=lowbit(x);}
int query(int pos)
{
int ans=0;
while(pos)ans+=datas[pos],pos-=lowbit(pos);
return ans;
}
}tree1,tree2;//封装起来减少码量（懒
signed main()
{
scanf("%lld%lld",&n,&m);
tree1.num=tree2.num=n;
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)
{
tree1.add(i,a[i]-a[i-1]);
tree2.add(i,(a[i]-a[i-1])*(i-1));
}
for(int i=1;i<=m;i++)
{
int opt,x,y,k;
scanf("%lld",&opt);
if(opt==1)
{
scanf("%lld%lld%lld",&x,&y,&k);
tree1.add(x,k);tree1.add(y+1,-k);
tree2.add(x,(x-1)*k);tree2.add(y+1,-y*k);
}
else
{
scanf("%lld%lld",&x,&y);
printf("%lld\n",tree1.query(y)*y-tree1.query(x-1)*(x-1)-tree2.query(y)+tree2.query(x-1));//那一大堆询问拆开就长这样qwq
}
}
return 0;
}
4. 树状数组求逆序对
这里简单说一下思路。
首先我们发现逆序对只与相对大小有关，于是我们先对原数据离散化一下。
然后按照下标顺序依次加入元素, 每次查询已经放到树状数组里的值比它大的元素的个数就行了.
贴一下代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define int long long
using namespace std;
struct node{int pos,x;}a[500010];
int rk[500010];
bool cmp(node xx,node yy)
{
if(xx.x!=yy.x)return xx.x<yy.x;
return xx.pos<yy.pos;
}
class Bittree
{
public:
int num=500010,datas[500010];
int lowbit(int x){return x&(-x);}
void add(int x,int k){while(x<=num)datas[x]+=k,x+=lowbit(x);}
int query(int pos)
{
int ans=0;
while(pos)ans+=datas[pos],pos-=lowbit(pos);
return ans;
}
}tree;
int n,ans;
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i].x);
a[i].pos=i;
}
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)rk[a[i].pos]=i;
for(int i=1;i<=n;i++)
{
tree.add(rk[i],1);
ans+=i-tree.query(rk[i]);
}
printf("%lld",ans);
return 0;
}
另：鉴于树状数组求最大最小值要做到\(O(n\log^2n)\)，就不做介绍了。
