bzoj2376/poj3350 保龄球
单调队列优化DP和处理边界情况好题,模拟赛后挂了好几发才过(雾)
这是一篇不完全算题解的解题报告(雾)
Description
你一个人去保龄球馆去打保龄球。总共有 \(k\) 个球可用。每个球的宽度为 \(w\)。在你前方有 \(n\) 个球棒要打。这 \(n\) 球棒紧密的排成一行,且第 \(i\) 个球棒宽度为 \(1\),价值为 \(x_{i}\)。你的每个球恰能击中第 \(a\) 个 \(\sim\) \(a+w-1\) 个的球棒(如果此球棒存在的话)。球棒被打到就倒了,且互不影响。你可以向任意方向击球,甚至球的一部分可以越过最左、最右边球棒所构成的边界。求最大价值。
Constraints
\(1≤n≤10000\),\(1≤w≤100\),\(1≤k≤500\),\(x_{i}\) 会有负数。
Solution
不难想到用 DP 来做,设 \(f[i][j]\) 表示考虑前 \(i\) 个球棒至多用 \(j\) 个球(不一定全用完) 的最大价值,但由于打掉一些球棒后会出现后效性,需要修改状态设计。
如果我们强制要求第 \(i\) 个球棒必须在这一轮打掉,则前面的状态得以确定,并且不会影响这一次的状态。
所以状态设计改为:考虑 \(f[i][j]\) 表示考虑前 \(i\) 个球棒,且必要在这轮打倒第 \(i\) 个球棒,至多用 \(j\) 个球的最大价值。
枚举 \(k\),上一次打到了哪里,分与这一次的打没有或又重叠两部分(重叠的意思就是这一次打不到完整的 \(w\) 个球棒),分开转移。
-
如果 \(k \lt i - w\),无重叠,这次可以获得 \(sum(i - w, i)\) 的价值。
-
如果 \(k \ge i - w\),会有重叠,这次可以获得 \(sum(k, i)\) 的价值。
初始值一开始全为 \(-INF\), 对于每个位置 \(i\),如果只打一个球就是长度为 \(w\) 的一段,\(f[i][1] = sum[i] - sum[max(i - w, 0)]\)。
时间复杂度为:\(O(N^2K)\)。
主要代码如下:(题干中的 \(k\) 为 \(kk\)。注意,这个代码只有 \(0\) 分,因为还未考虑全)

但是,样例通过了,交上去:

我们开始思考,是哪里的边界没有处理好?
面向数据,看看第一组数据:
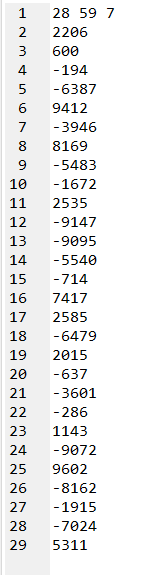
正解:\(17858\),输出:\(12547\)。
调试看出,程序只是计算出了前面的最大值,而最后单独从右边打掉 \(1\) 个的 \(5311\) 没有计算。
为了解决右边的极端情况,我们可以考虑右边再加 \(k\) 个虚拟球棒,价值均为 \(0\),转移时一起转移,最后取 \(\max\) 时也延长到 \(n + k\)即可。
scanf("%lld%lld%lld", &n, &kk, &w);
memset(f, ~0x3f, sizeof f);
for(int i = 1; i <= n; i++)
{
scanf("%lld", &a[i]);
sum[i] = sum[i - 1] + a[i];
f[i][1] = sum[i] - sum[max(i - w, (long long)0)];
}
for(int i = n + 1; i <= n + kk; i++)
{
sum[i] = sum[i - 1];
f[i][1] = sum[i] - sum[max(i - w, (long long)0)];//延长部分也要预处理
}
for(int j = 1; j <= kk; j++)
{
for(int i = 1; i <= n + kk; i++)//转移也要到 n + kk
{
f[i][j] = max(f[i][j], f[i][j - 1]);
for(int k = 0; k <= i - 1; k++)
{
if(k >= i - w)
f[i][j] = max(f[i][j], f[k][j - 1] + sum[i] - sum[k]);
else
f[i][j] = max(f[i][j], f[k][j - 1] + sum[i] - sum[i - w]);
}
}
}
int ans = 0;
rep(i, 1, n + kk)
rep(j, 0, kk)
ans = max(ans, f[i][j]);
printf("%lld", ans);
由于复杂度太大,还是在第 3 个点上 TLE 了。

考虑是否能优化。状态无法优化,只能考虑转移优化。
把方程写出来:
对于第一种转移,发现 \(sum[i] - sum[i - w]\) 为定值, \(k\) 只会影响 \(f[k][j -1]\),我们可以再设一个数组 \(maxn[i][j]\),表示 \(f[i][j-1](1 \le i \le i - w)\) 的最大值,转移时也带上 \(maxn\) 数组转移即可,这样这种转移复杂度为 \(O(1)\)。
对于第二种转移,\(k\) 会影响里面大多元素,但是,在 \(i\) 向后枚举递增时,我们需要的 \(k\) 的区间也在递增,不难啊想到用单调队列优化转移。
\(sum[i]\) 为定值,那我们把 \(f[k][j - 1] - sum[k]\) 放入单调队列里,我们需要的区间即为 \(k > i - w\),在转移时更新单调队列的头尾指针即可。
// by youyou2007 in 2022.
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#include <map>
#define int long long
#define REP(i, x, y) for(int i = x; i < y; i++)
#define rep(i, x, y) for(int i = x; i <= y; i++)
#define PER(i, x, y) for(int i = x; i > y; i--)
#define per(i, x, y) for(int i = x; i >= y; i--)
#define lc (k << 1)
#define rc (k << 1 | 1)
using namespace std;
/*
考虑 f[i][j] 表示前 i 个位置且 i 位置必打,用 j 个球打的最大分数
f[i][j] = max(f[k][j - 1]) + sum(j - k + 1 ~ k)
注意要到 n + k,因为考虑左右区间极端情况
*/
const int N = 10005 + 505;
const int K = 505;
int n, kk, w;
int f[N][K], maxn[N][K];
int sum[N], a[N];
int que[N * 2], head, tail;
signed main()
{
scanf("%lld%lld%lld", &n, &kk, &w);
memset(f, ~0x3f, sizeof f);
memset(maxn, ~0x3f, sizeof maxn);
for(int i = 1; i <= n; i++)
{
scanf("%lld", &a[i]);
sum[i] = sum[i - 1] + a[i];
f[i][1] = sum[i] - sum[max(i - w, (long long)0)];
maxn[i][1] = max(maxn[i - 1][1], f[i][1]);
}
for(int i = n + 1; i <= n + kk; i++)
{
sum[i] = sum[i - 1];
f[i][1] = sum[i] - sum[max(i - w, (long long)0)];
maxn[i][1] = max(maxn[i - 1][1], f[i][1]);
}
for(int j = 2; j <= kk; j++)
{
head = 0, tail = 1;
for(int i = 1; i <= n + kk; i++)
{
/* f[i][j] = max(f[i][j], f[i][j - 1]);
for(int k = 0; k <= i - 1; k++)
{
if(k >= i - w)
f[i][j] = max(f[i][j], f[k][j - 1] + sum[i] - sum[k]);
else
f[i][j] = max(f[i][j], f[k][j - 1] + sum[i] - sum[i - w]);
}*/
if(i <= w)
{
f[i][j] = sum[i];
}
else
{
f[i][j] = max(f[i][j], maxn[i - w][j - 1] + sum[i] - sum[i - w]);
while(head <= tail && que[head] < i - w)
{
head++;
}
while(head <= tail && f[i][j - 1] - sum[i] > f[que[tail]][j - 1] - sum[que[tail]])
{
tail--;
}
que[++tail] = i;
f[i][j] = max(f[i][j], f[que[head]][j - 1] + sum[i] - sum[que[head]]);
}
maxn[i][j] = max(maxn[i - 1][j], f[i][j]);
}
}
int ans = 0;
rep(i, 1, n + kk)
rep(j, 0, kk)
ans = max(ans, f[i][j]);
printf("%lld", ans);
return 0;
}



