P7074 [CSP-J2020] 方格取数
Description
给定一个 \(n*m\) 的矩阵，每个格子里有一个数，每次只能向上、下、右走一步，不能走走过的格子，问从左上角走到右下角可以取到的最大值。
Limit
\(n,m \le 1000\)。
Solution
Solution 1 DP
这题与某年前的方格取数很像，但由于这题可以上下走，所以有后效性，要转换思路。
发现虽然能上下乱跑，且走完一列之后只能向右走，所以可以把这个矩阵划分为 \(m\) 列，由此设方程。
又因为不能走回头路，所以在进入新的一列之后，要么只向上走，要么只向下走，要么再向右走一列。
设计状态:设 \(f[i][j]\) 表示在第i行，第j列的位置，且下一步必定向右走（即到 \((i,j+1)\)）可取到的最大价值。
很轻易地得到初始值：\(f[i][1] = \sum_{S=j}^{i} a[j][1]\)
考虑每个点如何从前一列转移来：
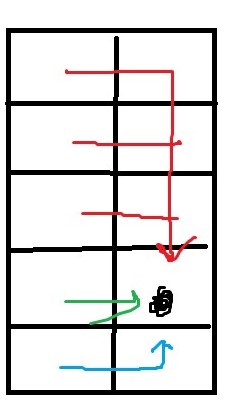
据这个图可知，每个点从左边来有三种方式：
-
直接从左边走过来。（绿）
-
先从左边跳到这一列，再从上面走下来。（红）
-
先从左边跳到这一列，再从下面走上来。（蓝）
对这几种情况分别转移，为了转移方便，我们可以把左边的那一种情况给并到其他两种情况，答案不会改变。
上面转移情况：
可以从第 \(1\) 行枚举到 \(n\) 行，维护这一列的前缀和，则上面每一个得到的值就是前面的列中且结束在第i行的最大值+这一列向下走的过程中取的数之和。
设现在要求第 \(j\) 列第 \(i\) 行，已经枚举到了第\(k\)行，\(temp\) 就表示 \(\max\){\(f[i][j - 1]\)} + \(\sum_{S=k}^{j} a[i][S]\)
即 \(temp = max(temp, f[i][j - 1]) + a[i][j]\)。
转移方程： \(f[i][j] = max(f[i][j], temp)\)。
下面转移情况：
同上面转移，只不过反过来枚举 \(i\)。
即 \(temp = max(temp, f[i][j - 1]) + a[i][j]\)
转移方程\(f[i][j] = max(f[i][j], temp)\)
Code：
// by youyou2007 Aug.
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#define REP(i, x, y) for(register int i = x; i < y; i++)
#define rep(i, x, y) for(register int i = x; i <= y; i++)
#define PER(i, x, y) for(register int i = x; i > y; i--)
#define per(i, x, y) for(register int i = x; i >= y; i--)
#define lc (k << 1)
#define rc (k << 1 | 1)
using namespace std;
#define int long long//会爆int
const int N = 1005;
int n, m;
int f[N][N], a[N][N];
signed main()
{
scanf("%lld%lld", &n, &m);
rep(i, 1, n)
{
rep(j, 1, m)
{
scanf("%lld", &a[i][j]);
}
}
memset(f, -0x3f, sizeof f);
f[1][0] = 0;
f[1][1] = a[1][1];
rep(j, 1, m)
{
int temp = -99999999999999999;
rep(i, 1, n)
{
// if(i == 1 && j == 1) continue;
temp = max(temp, f[i][j - 1]) + a[i][j];
f[i][j] = max(f[i][j], temp);
}
temp = -9999999999999999;
per(i, n, 1)
{
// if(i == 1 && j == 1) continue;
temp = max(temp, f[i][j - 1]) + a[i][j];
f[i][j] = max(f[i][j], temp);
}
}
cout << f[n][m];
return 0
}
Solution 2 记忆化搜索
既然DP是顺推的，当然可以记忆化搜索逆推！
设 \(f[i][j][0]\) 表示当前在第 \(i\) 行第 \(j\) 列且从格子上（0）/下（1）方走到该格子的最大价值。
则上下的这两种情况可以解决了。
现在要考虑从左边过来的情况，但由于左边没有限制，所以从左上或左下来的转移都是可以的。
所以
- \(f[i][j][0]=max(dfs(x - 1, y, 0), dfs(x, y - 1, 0), dfs(x, y - 1, 1)) + a[x][y]\)
这是上一步从上方转移的情况，由于不能走回头路，所以不能从下方转移。上面三个搜索分别是上方、左上方、左下方转移来。
- \(f[x][y][1] = max(dfs(x + 1, y, 1), max(dfs(x, y - 1, 0), dfs(x, y - 1, 1))) + a[x][y]\)
从下方转移同理，上面三个搜索分别是上方、左上方、左下方转移来。
Code
// by youyou2007 Aug.
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#define REP(i, x, y) for(register int i = x; i < y; i++)
#define rep(i, x, y) for(register int i = x; i <= y; i++)
#define PER(i, x, y) for(register int i = x; i > y; i--)
#define per(i, x, y) for(register int i = x; i >= y; i--)
#define lc (k << 1)
#define rc (k << 1 | 1)
using namespace std;
#define int long long
const int N = 1005;
const int MINN = -999999999999999;
int n, m;
int f[N][N][3], a[N][N];
int dfs(int x, int y, int from)
{
if(x <= 0 || y <= 0 || x > n || y > m) return MINN;
if(f[x][y][from] != MINN) return f[x][y][from];
if(from == 0)
{
return f[x][y][from] = max(dfs(x - 1, y, 0), max(dfs(x, y - 1, 0), dfs(x, y - 1, 1))) + a[x][y];
}
else
{
return f[x][y][from] = max(dfs(x + 1, y, 1), max(dfs(x, y - 1, 0), dfs(x, y - 1, 1))) + a[x][y];
}
}
signed main()
{
scanf("%lld%lld", &n, &m);
rep(i, 1, n)
{
rep(j, 1, m)
{
scanf("%lld", &a[i][j]);
f[i][j][0] = f[i][j][1] = MINN;
}
}
f[1][1][0] = f[1][1][1] = a[1][1];
dfs(n, m, 0);
cout << max(f[n][m][1], f[n][m][0]);
return 0;
}
