sd1

0、beit

vision Transform 用 dvae 做图像的编码和解码 

dvae：

 

 

1、beit2

linear probe ： 通过将最后一层替换成线性层，并只训练该线性层

vqkd：

如果仅仅 evaluate，则算完 cluster_size 之后，上面的（更新codebook）就不进行了。

 

 

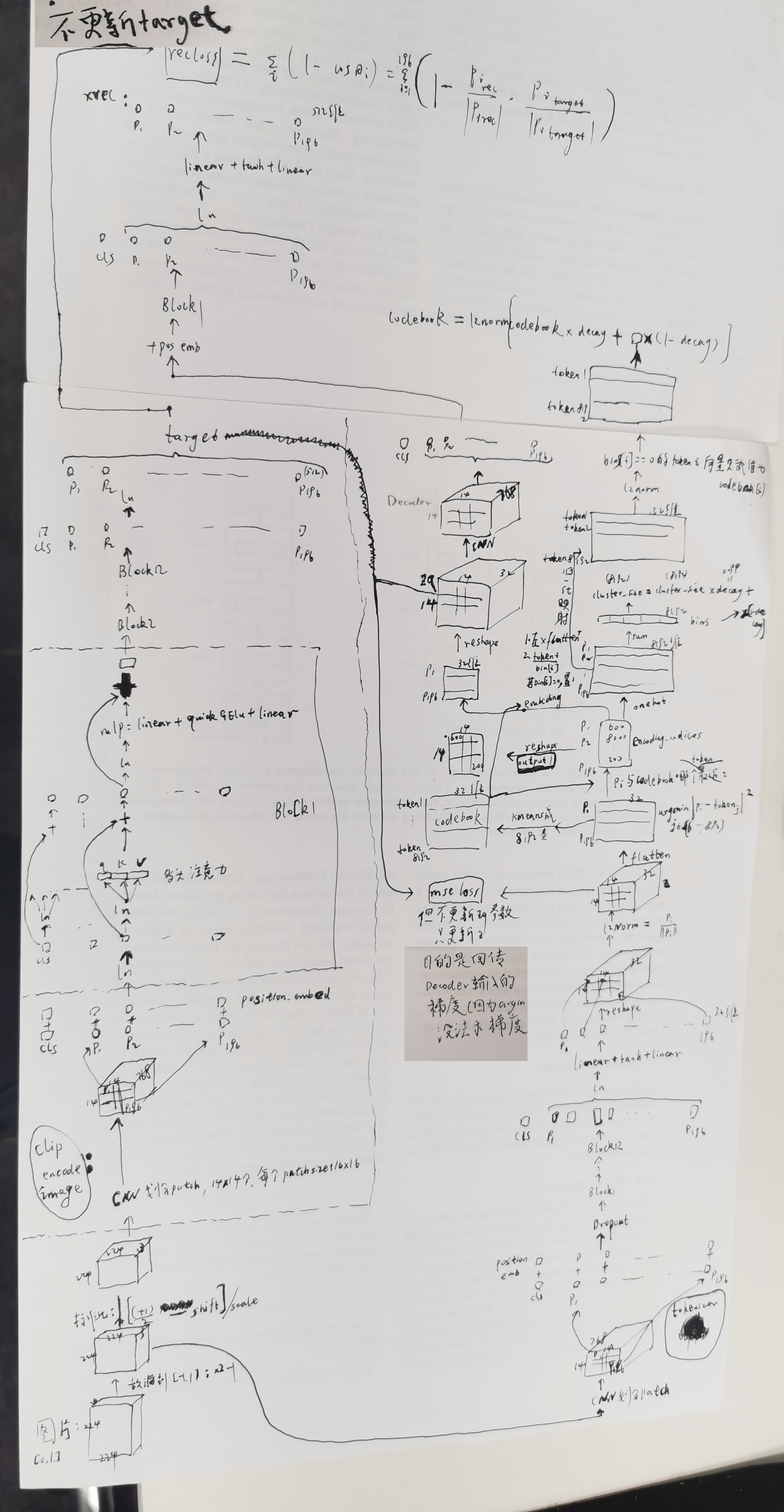
 beit2：

从CNN划分batch到block9出来，再去掉mask机制是原本纯粹的VIT结构，vit 中间的位置编码可以是相对位置，也可以是别的，vit 输入图片的patch们+1个cls，输出1个cls向量+patch们的向量

其中相对位置编码：

https://zhuanlan.zhihu.com/p/444807223

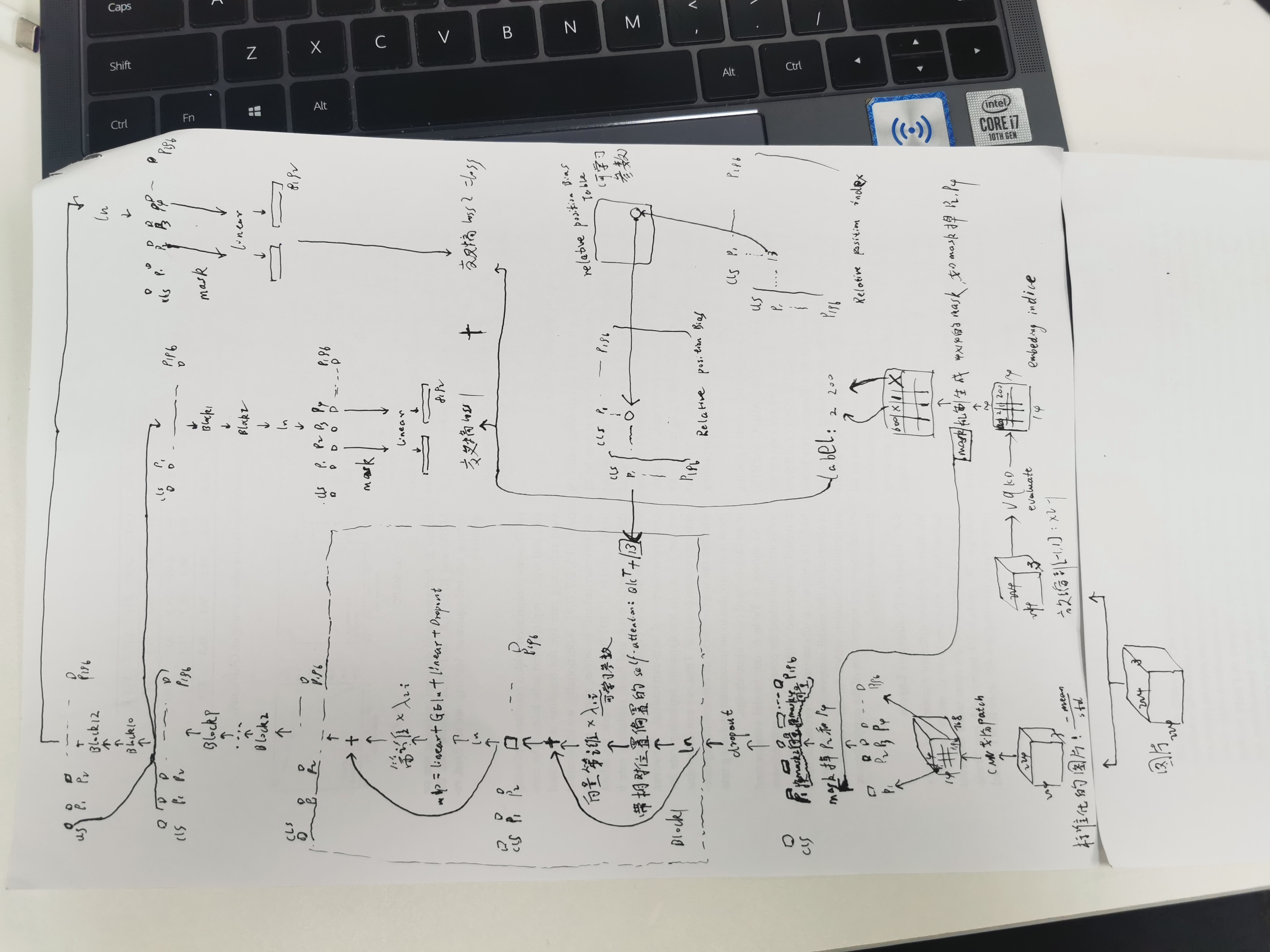
 分类和语义分割：

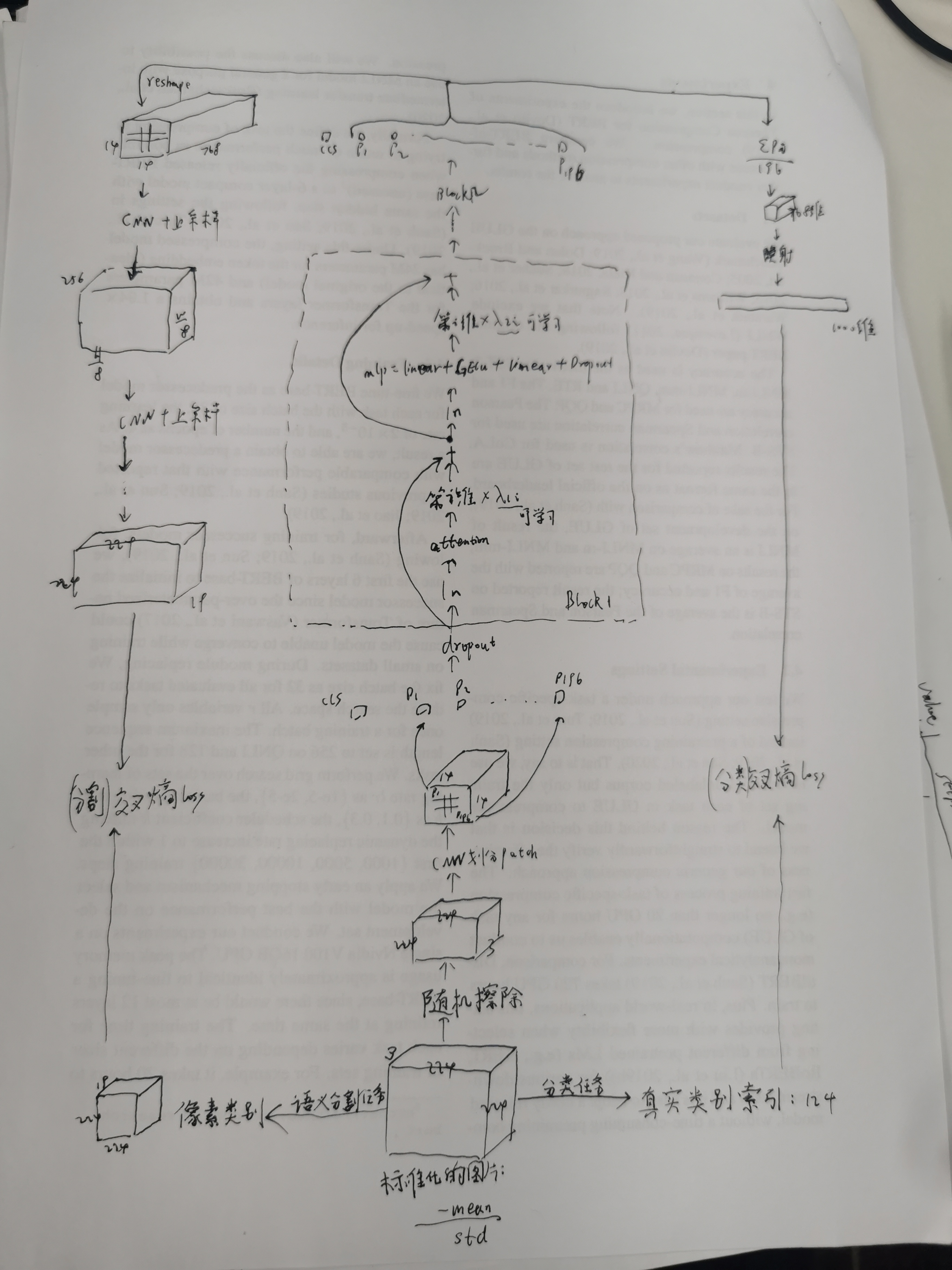
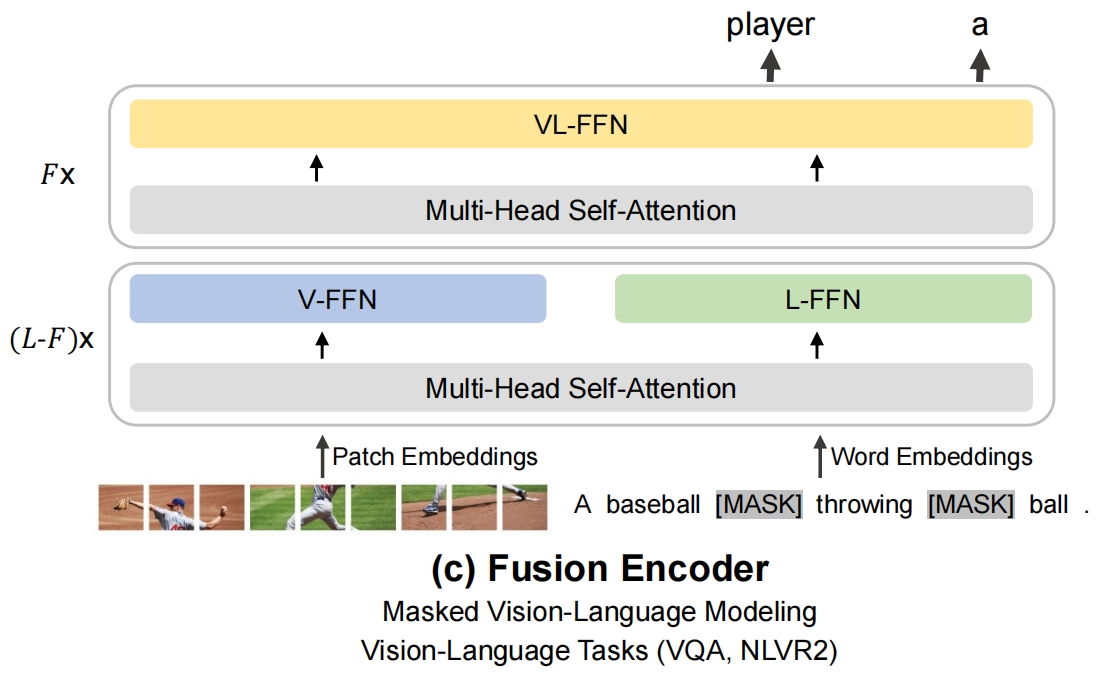
2、Beit3

tokenizer 用 Beit2的

 

 

 

3、ddpm

 包括：扩散过程（forward process，x0->xT,给图像加噪声，使得模型学会拆楼的能力）、逆扩散过程（reverse process，xT->x0，从噪声图像中生成图像，即使得模型学会建楼的能力）

假定扩散过程是马尔科夫过程，不含待求参数，αt和βt是提前定义好的超参数，βt从0.0001 线性增长到 0.02 ：

 

根据贝叶斯公式得到后验（抽了xt,x0以后再求的分布）分布q(xt-1|xt,x0)！该分布自然是不含参数的：

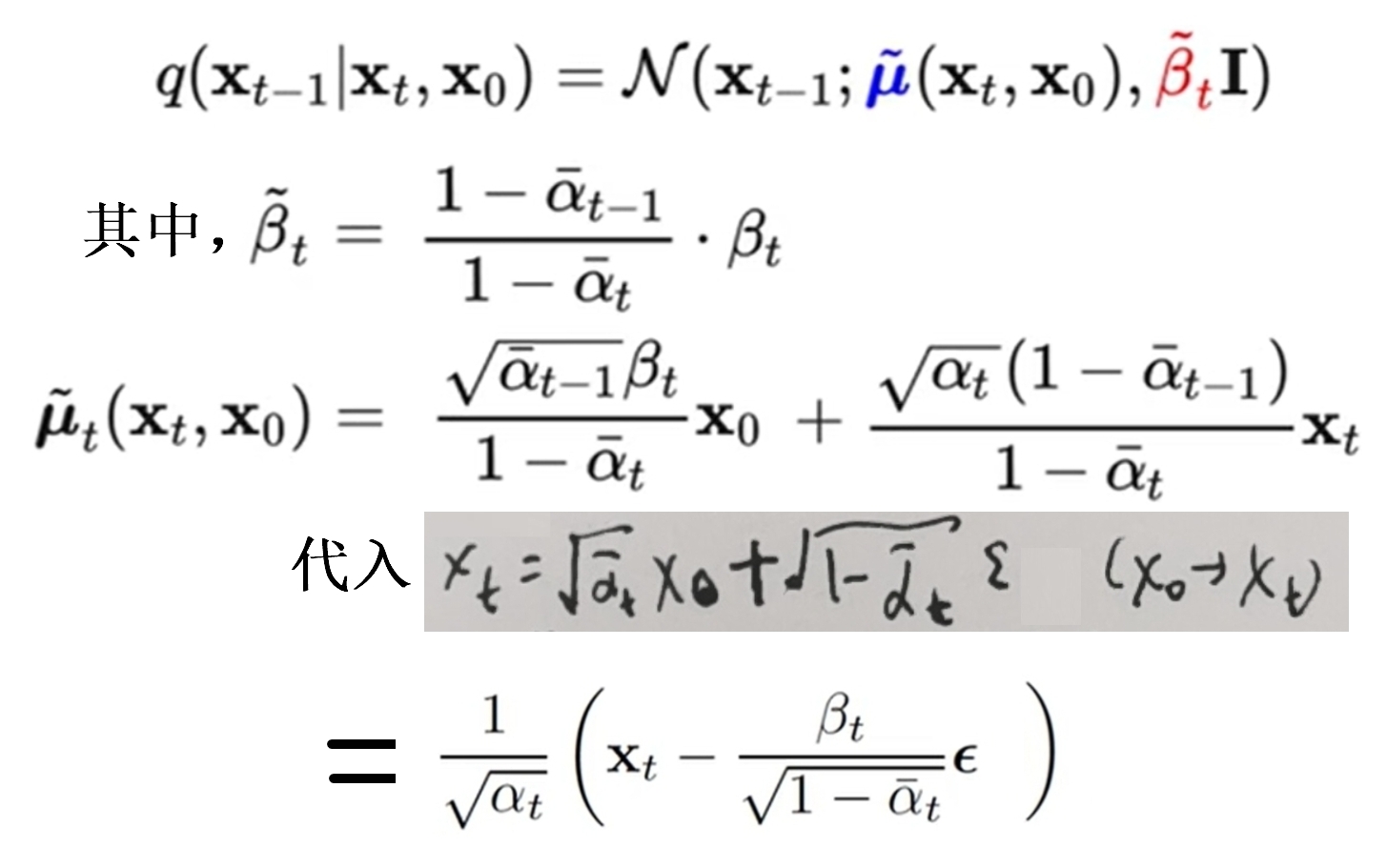
 最终得到的XT服从N(0,1)

根据贝叶斯公式，真实的逆分布q(xt-1|xt)在 当数据集X0只有1个样本时，该逆分布的方差是 βt~；当数据集服从标准正态分布，此时方差就是 βt

（1）第1种思路：

 假定逆扩散过程是马尔科夫过程， pθ(xt-1 | xt) 是高斯分布N(uθ，方差θ)，希望该分布能在各种时刻和已知的q(xt-1|xt,x0)的分布一样，所以令uθ形式上和u~一样，只不过把噪声eps换成epsθ，然后对任意时间从真实分布q(xt|x0)中采样到的xt，训练epsθ逼近和eps。直接令方差θ=βt~或者βt，不含参数θ。定义含参的均值表达式：

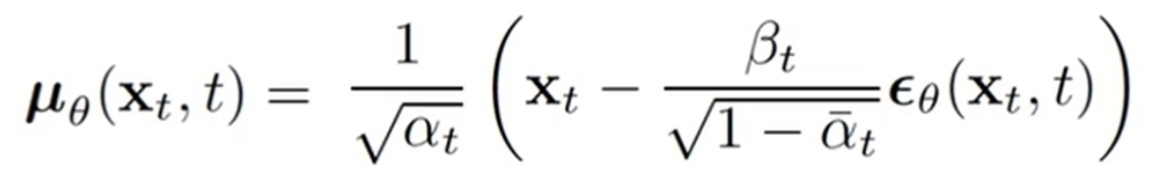
希望 pθ(xt-1 | xt)  和 后验分布q(xt-1 | x0,xt) 分布的均值一致，即噪声eps和人工噪声epsθ一致，从而得到最后的噪声差的损失函数，其中 t 的范围是{1,...,T}，X0是原始数据集，理论上要迭代够这三个大集合：

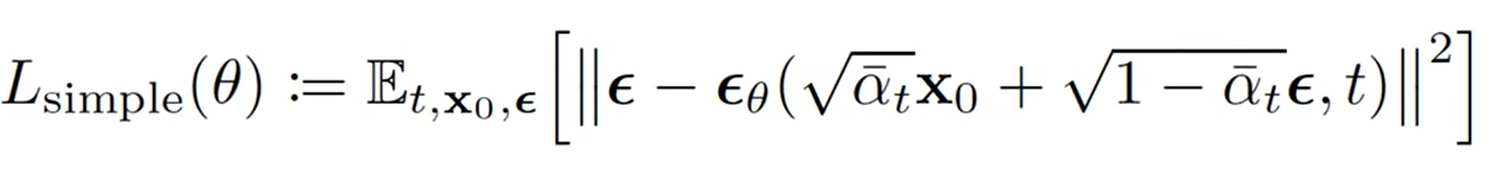
本质上是在让epsθ模型学会拟合扩散过程是怎么加噪的

（2）第2种思路：

假定逆扩散过程是马尔科夫过程， pθ(xt-1 | xt) 是高斯分布N(uθ，方差θ)，感觉该分布的均值能和 q(xt|xt-1)的xt-1类似， 所以定义均值θ为：

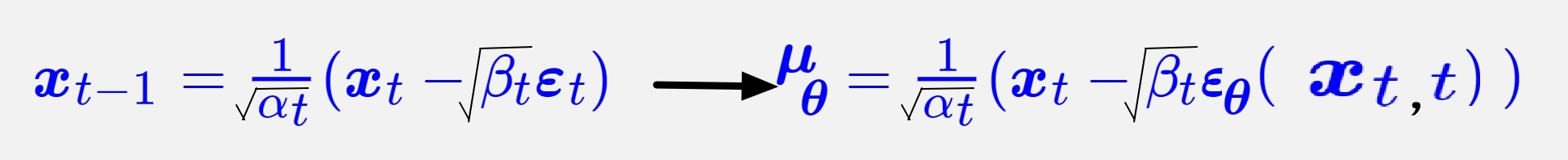
思路2.1：训练epsθ逼近和eps，直接令方差θ=βt~或者βt，可以得到Lsimple 表达式

思路2.2：

正向和逆向都有对应的联合分布：

加噪：q(x0,x1,x2,⋯,xT)=q(xT|xT−1)⋯q(x2|x1)q(x1|x0)q~(x0)，q~(x0)是原来数据集分布

解噪：pθ(x0,x1,x2,⋯,xT)=pθ(x0|x1)⋯pθ(xT−2|xT−1)pθ(xT−1|xT)pθ(xT)，p(xT)是N(0,1)正态分布

希望两者分布一致，所以令两者的KL散度逼近0，也能得到 Lsimple 的形式

（3）第3种思路：基于贝叶斯定理

只考虑1个前向的高斯分布，如果把 q(xt-1|xt,x0)的x0去掉，那就能直接代入该公式进行采样了。如果成功训练一个uθ(xt)能逼近x0，那么q(xt-1|xt,x0)≈q(xt-1|xt,uθ(xt))=q(xt-1|xt)，就能从 q(xt-1|xt) 中采样了

根据q(xt|x0)的x0的表达式定义uθ(xt)：

 

 定义损失函数 = ||x0-uθ||2，最后也能推出Lsimple

 

 

 

训练：目的是要训练出1个epsθ模型逼近随机噪声eps，过程是先要随机取个原始样本x0，然后在{1,2,3...,T}中随机取个时间 t，随机噪音eps，根据真实分布q(xt|x0)采样出对应的真实的xt，把xt和t传入到nn模型中输出人工噪声epsθ，两者求MSEloss并更新epsθ模型中的梯度，再随机取个原始样本...迭代，最终能定下来人工噪声epsθ模型，从而知道了pθ(xt-1 | xt) 的分布了

预测：随机取个二维向量噪声作为T时刻的数据，通过 分布 pθ(xt-1 | xt) 采样（利用重参数技巧）T-1时刻的样本，再T-2...直到X0，求出X0的分布后就不用采样了，直接拿x0的分布均值就当做预测的x0（没必要再偏移了）

 

预测噪声、原图、速度v都是等价的，不过在蒸馏时，采用v-prediction效果更好

4、iddpm

主要改进 ddpm： pθ(xt-1 | xt) 的方差可学习（新增1个VLB loss）、βt 由线性方案改为cos方案（在t=0和t=T的端点处加噪缓慢，在中间加噪是线性的，可以使得模型能看更看清图像）

训练过程：

 

 nn 模型采用Unet：

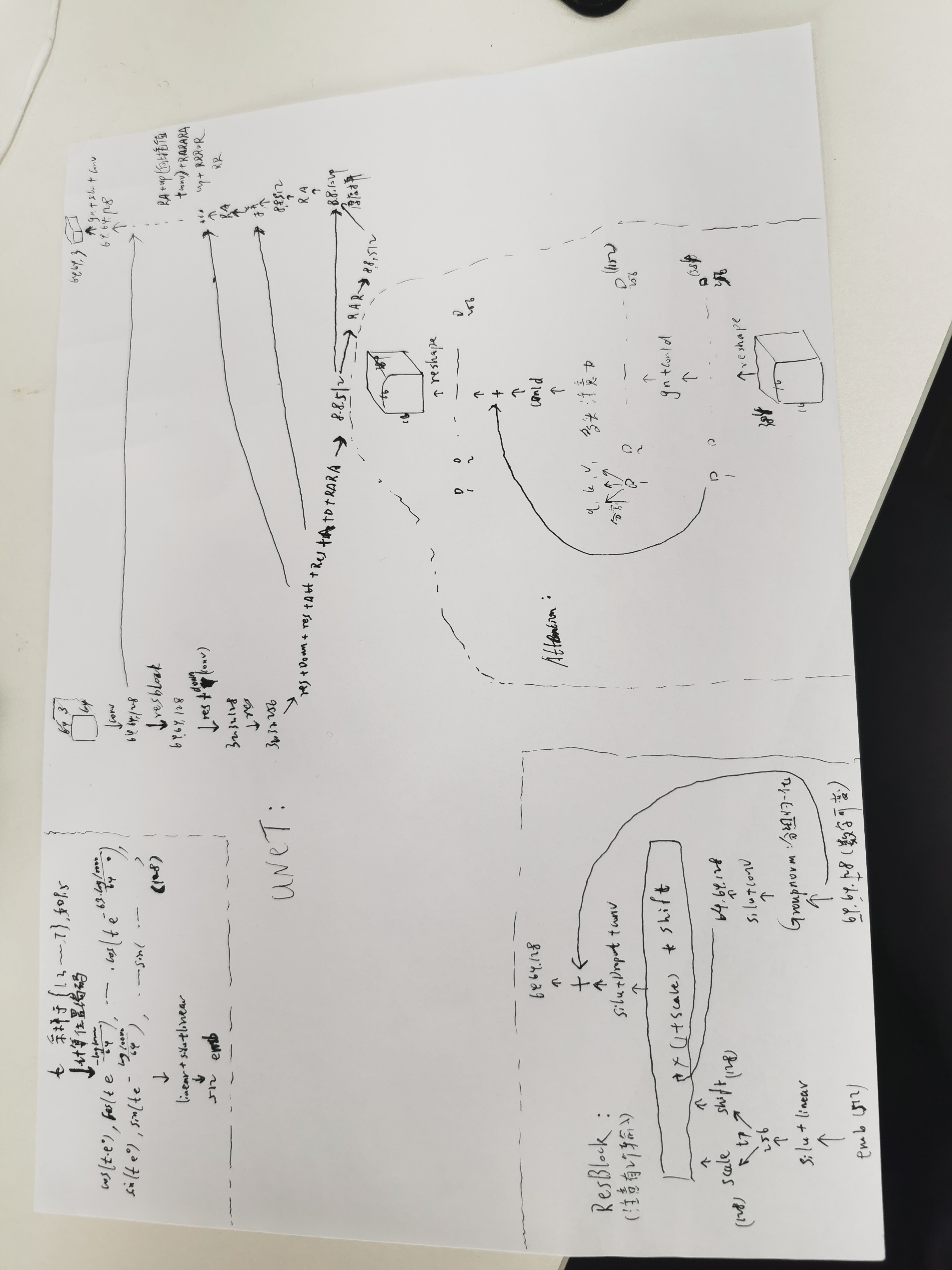
采样：

 

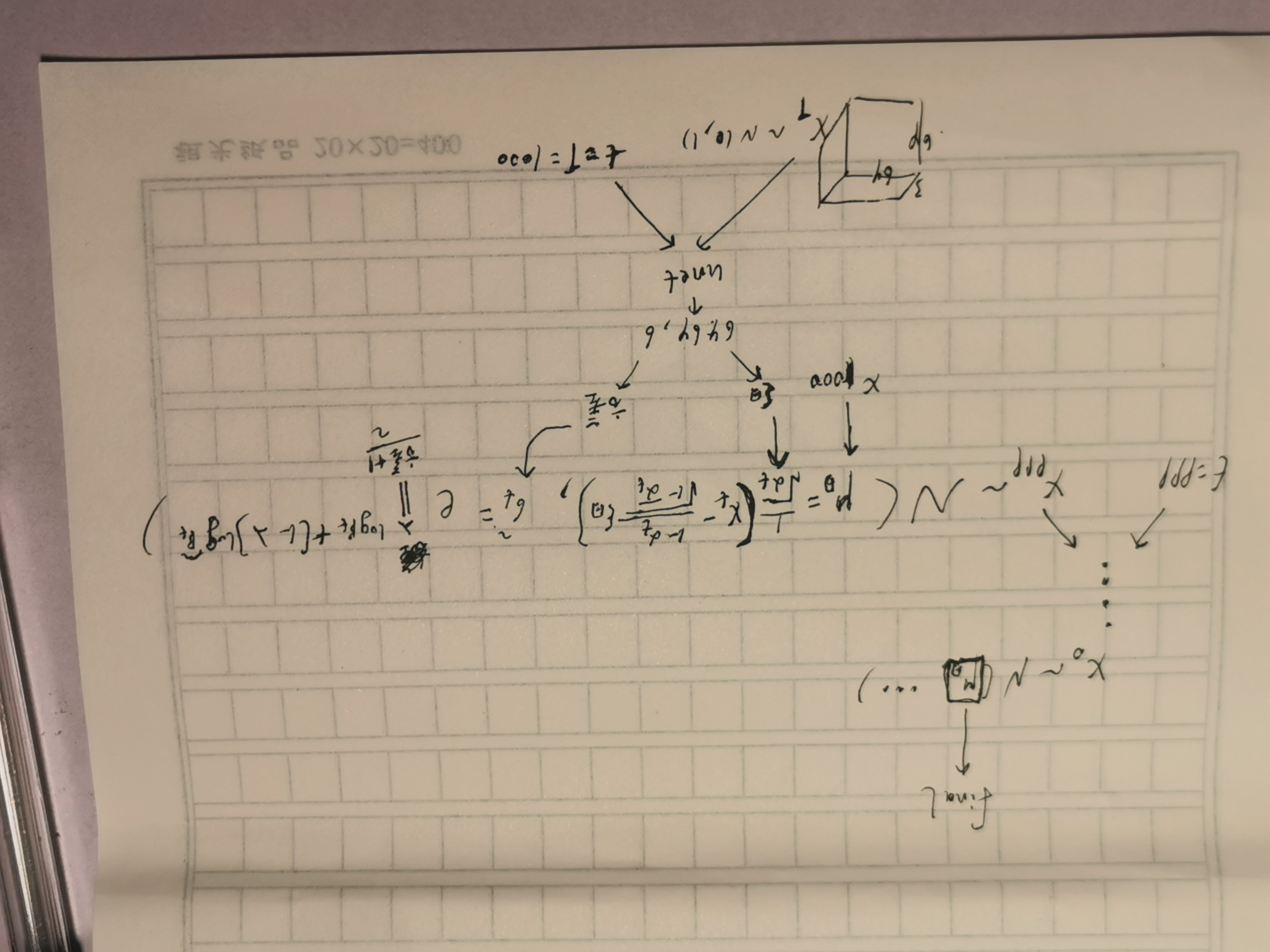
5、ddim

 

 

等式两边是两个分布，分别采样xt-1，再令两者相等，可以求出p(xt−1|xt,x0)的分布，此时只有 1个变量 σt ，可以取任意值，ddpm是其取某个值的特例

继续训练一个uθ(xt)能逼近x0，即epsθ逼近eps，此时训练过程和ddpm一模一样，可以直接用ddpm训练好的模型，之后可以得到 p(xt-1|xt,x0)≈p(xt-1|xt,uθ(xt))=p(xt-1|xt) 的分布，根据该分布进行采样就好了：

前向 xt->xt+1：

 

 

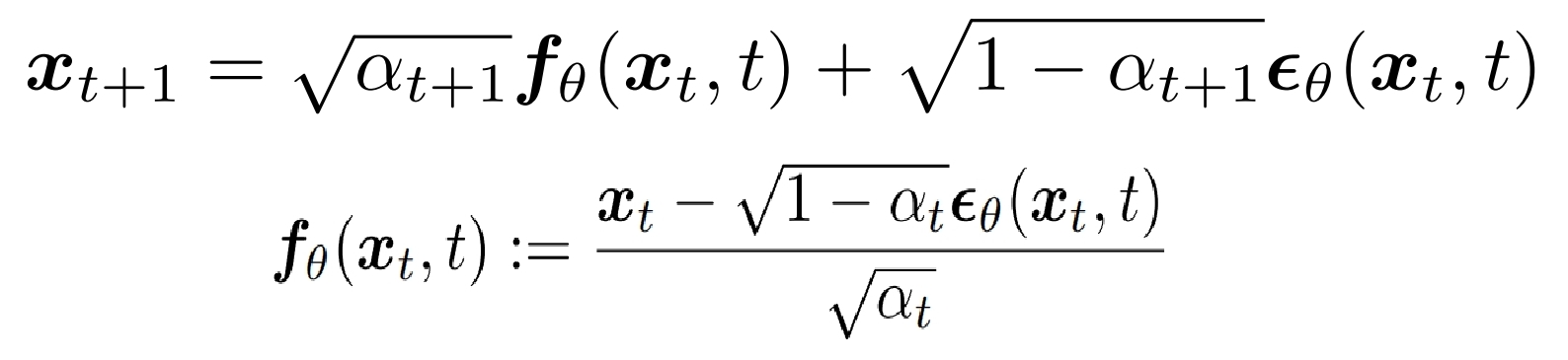
后向：

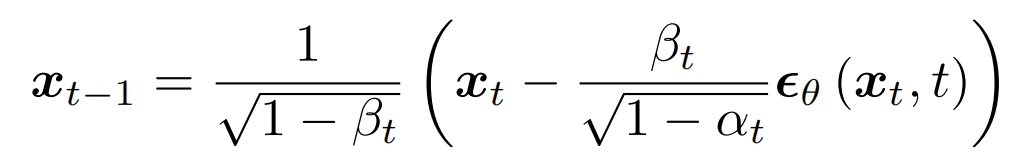
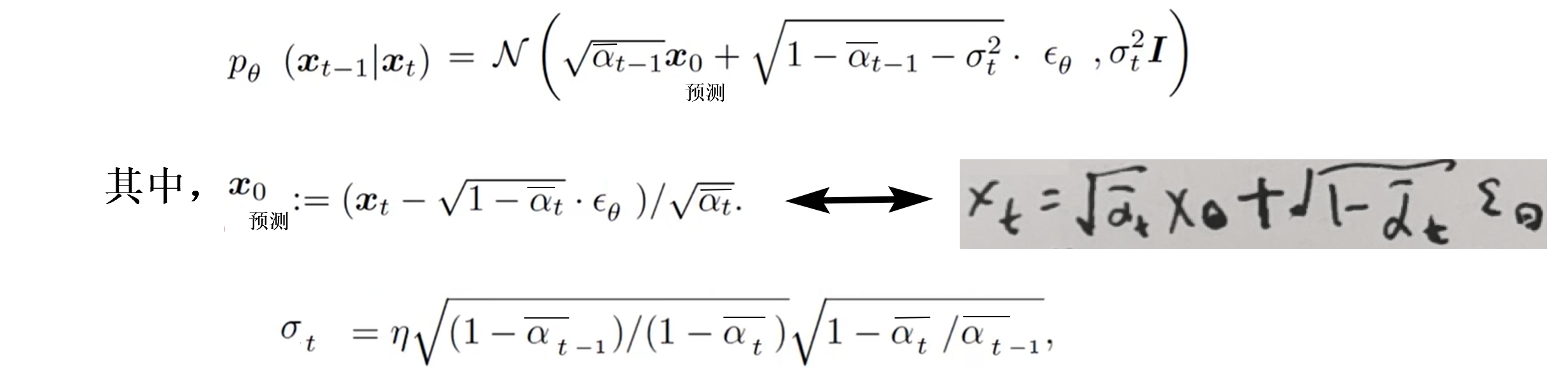
其中 σt 用一个式子表示，n可以取任意值，当取0时，σt =0，记为ddim，此时从xt到xt−1是一个确定性变换（无需采样了）

还引入了respacing方法，将连续采样变为间隔采样，具体实现：

 

6、LDM=latent diffusion model

 

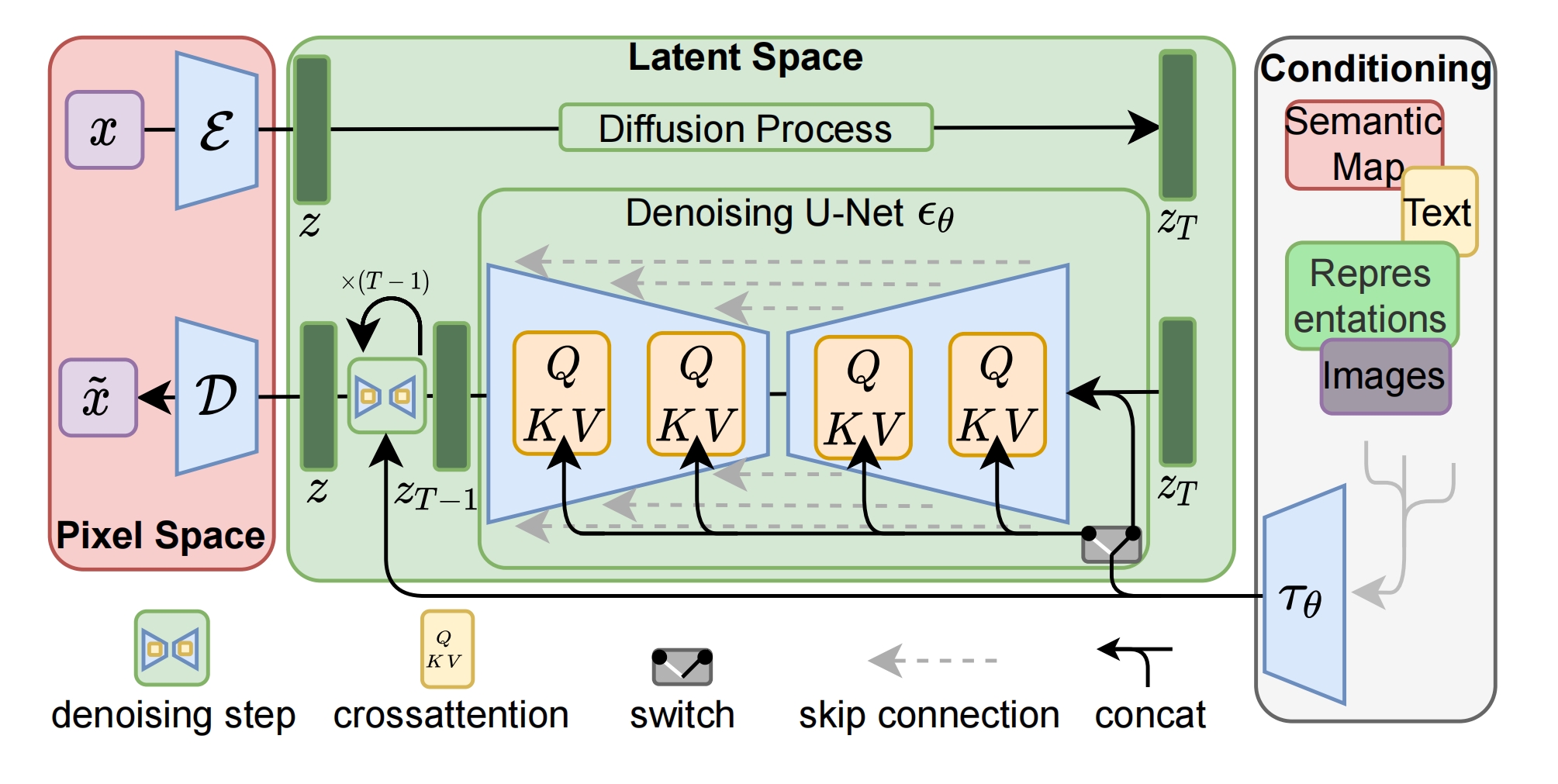
先通过编码器把图片 x 从像素空间映射到隐空间，在隐空间中使用DM（这是为了减少计算开销），把输入的文本、图片当做条件，通过注意力机制引入到nn模型中，此处采用unet，最后在像素空间通过解码器 D 恢复

7、分数扩散模型

给x0分别加均值为0，但是不同方差的正态分布的噪声来生成不同量级的噪声数据（注意ddpm是逐步的加），训练人工构造的 sθ ，即NCSC（noise conditional score network），在不同量级下都能够逼近真实分数（该方式叫做sorce matching），以期望逼近加任意噪声后的分布的分数，采样方式包括：欧拉数值采样，欧拉数值+郎之万采样，ODE采样。若将加噪看成是连续的过程，可以用SDE来表示分数扩散模型（VESDE）和ddpm（VPSDE）

训练：

 

 采样：