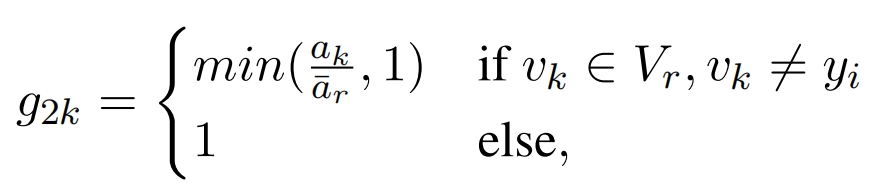各向异性
Transformer生成的各个词向量具有各项异性问题(anisotropic,representation degeneration problem),即词向量都聚集在一个狭小的锥形空间,任何两个词都具备相似度,这个可以通过对词向量矩阵做低秩近似到2维平面可以看出来(即将向量映射到二维),此处的低秩近似指的是:利用一个秩较低的矩阵来近似表达原矩阵,不但能保留原矩阵的主要特征,而且可以降低数据的存储空间和计算复杂度
这个问题产生的直观原因是:在序列生成任务中,模型要根据当前的隐向量预测出下一个单词,所以词向量就尽可能的和当前隐向量相似,从而导致该词向量与其他隐向量(空间中的大多数)离得很远,以致于龟缩到1个角落,这样所有的词向量都龟缩在这里了。数学原因:
红色的多边形(有内部)是点集Q的凸包(刚好包括)
定理1:隐向量集合的uniformly negative direction 向量v(v与集合内所有向量内积<0)存在《=》隐向量集合的凸包不含有原点
所以模型损失不仅要考虑原来的任务损失,还要考虑到各项异性问题(词向量的相似性损失)
解决方法1:将任何22之间的词向量相似度降低,即loss添加一个正则化项(叫做:MLE-CosReg),其中wi是词向量wi归一化后的结果:
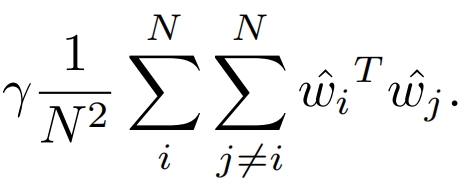
这是针对所有的词进行的,可能导致对高频词的过度正则化
解决方法2:低频词的梯度会导致低频词向量更加远离其他词向量从而造成退化,如果一开始就固定低频词向量,那么就能降低退化问题,其他词向量训练的会更好,但是低频词向量每怎么训练,所以对于低频词向量既要训练又不能训练太多,即要对低频词自适应计算梯度:
对于decoder的第 i 步,若实际词是yi,则根据3个 logit 来计算第 i 步的 loss:
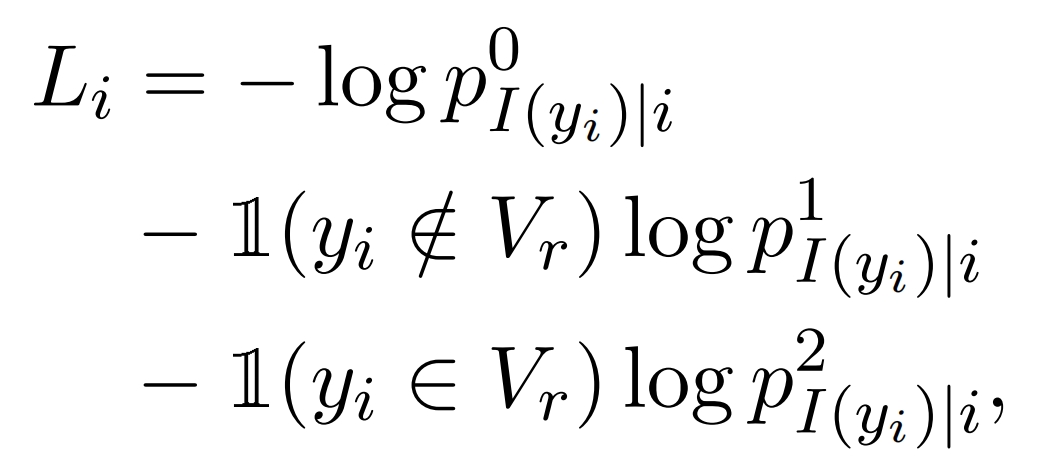
如果yi不属于低频词(词频小于某个参数,对词频词集合的定义可以是随着训练动态定义),则计算第1,2项,否则计算第 1,3 项。
第1项的p:第 i 步的隐向量* 不参与梯度运算的向量矩阵 映射到字典长度
![]()
再softmax,再找实际词yi 的概率
第2项和第3项的p:基于第 i 步的不参与梯度运算的隐向量 和 门机制 映射到字典长度,其中gl是一个控制向量,圆点符号表示元素独立的相乘,第二项用g1,第三项用g2
![]()
再softmax,再找实际词yi 的概率
g1用于控制低频词,g1的第k个分量对应字典第k个词vk,Vr是低频词集合,ak是vk的词频:
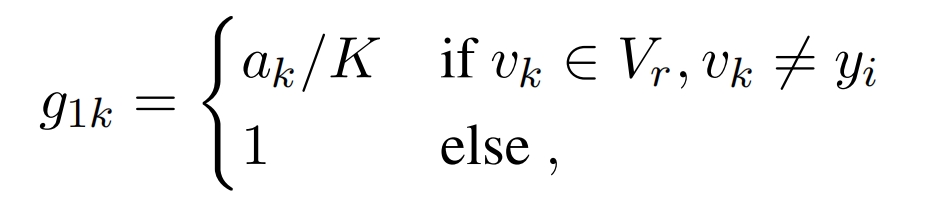
g2用于控制非常低频的低频词,g2的第k个分量对应字典第k个词,其中ar_是平均词频: