m7

1、随机过程数学知识

形式：样本空间={样本点1、样本点2...样本点n}，事件A={样本点1，样本点3}

 概率空间：

 

 

 

 

 

 

 

 

 

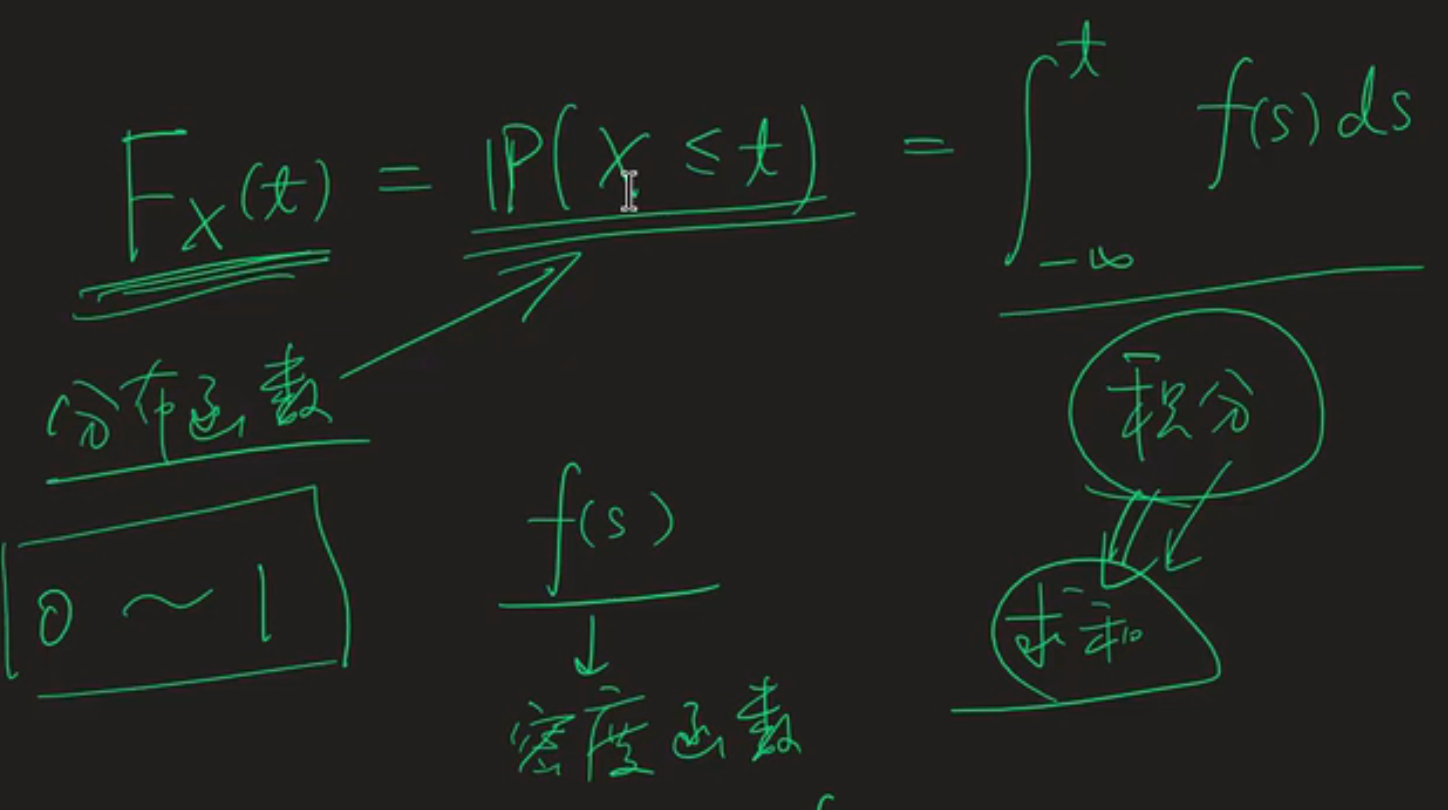
 随机向量：多维随机向量

随机过程比如股票价格，每个时间点是一个随机变量，有时间和状态，可以分类：

 

 

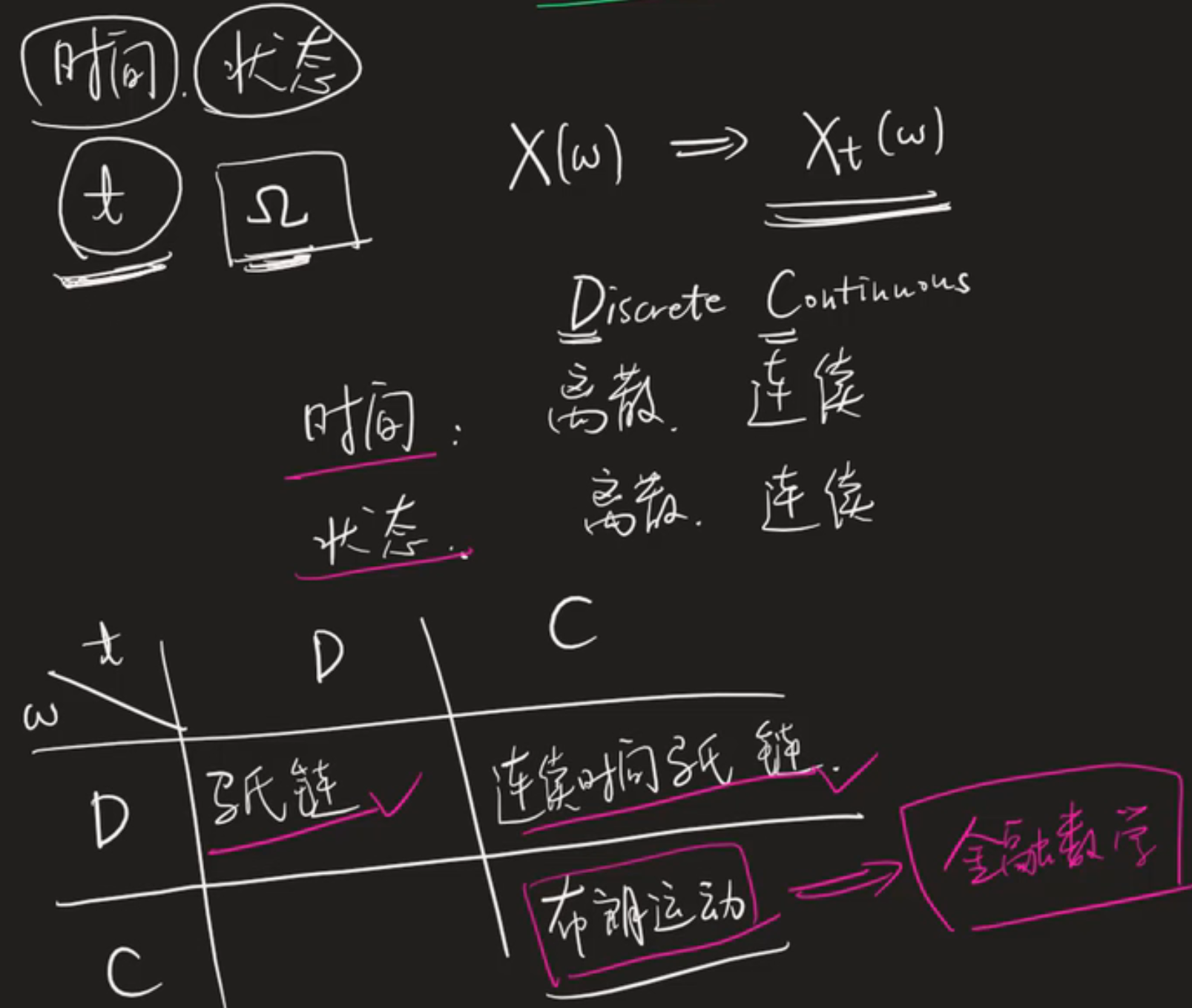
 固定状态，得到的随机过程的一次实现

离散型随机变量的期望：

 

 

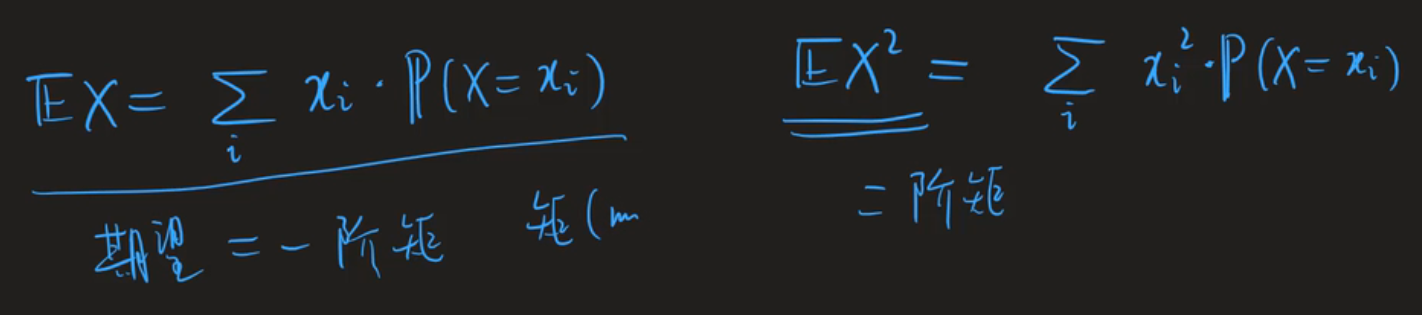
 连续的期望：

 

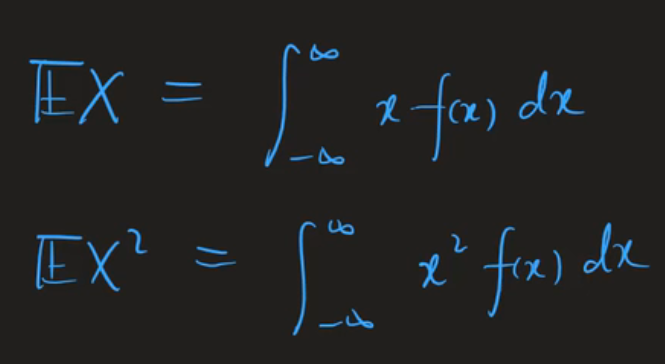
连续型随机变量的卷积公式可用于计算X+Y的分布函数，积分变量是 s ，即下图中U的分布函数： 

 

 

也可以用于计算X+Y的概率密度函数：

 

 

 

 

 

 X=0,1,2,3..，则

 

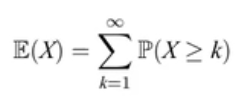
 X=0,1,2,3..，则概率母函数（下面的导数是对 s 求导）：

 

 

 

 

 

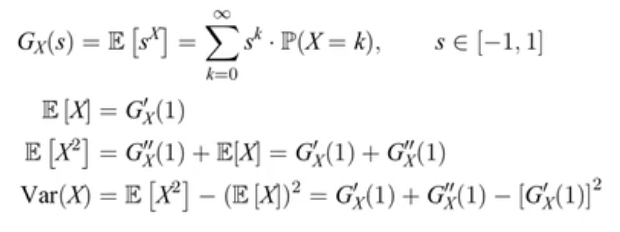
 连续型随机变量X，定义矩母函数及其性质：

 

 

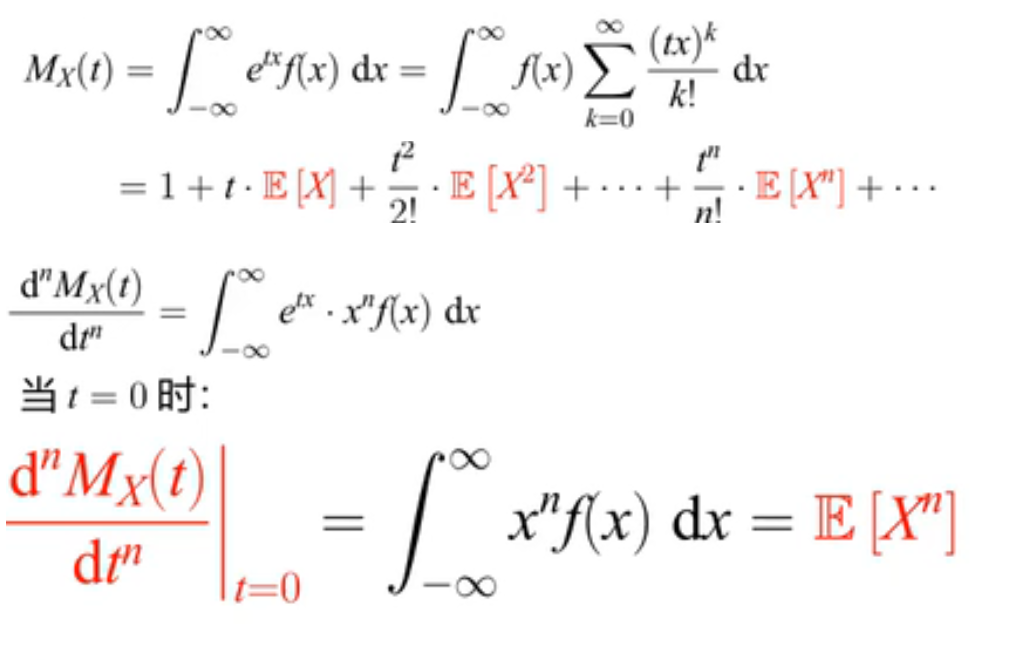
 【马尔科夫链】

马尔科夫性：未来状态只与当前有关，与以前无关

时齐性：一步转移概率与时间无关，只和状态有关

目前只学习满足马尔科夫性和时齐性的马尔科夫链

转移矩阵每行的元素之和=1，第（i,j）元素代表 i 状态经过n步转移到 j  状态的概率

p(m)ij： 从 i 经过m步转移到 j 的概率

m步转移矩阵是1步转移矩阵的m次幂

 

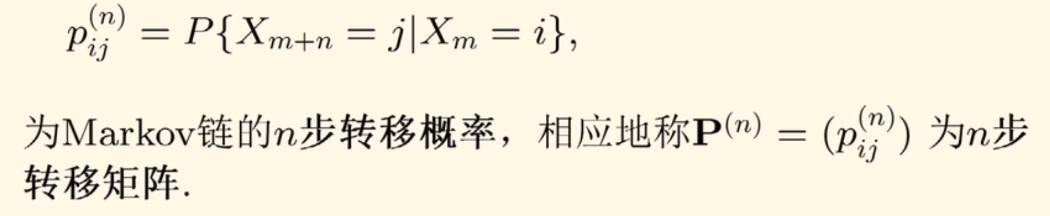
 CK方程：

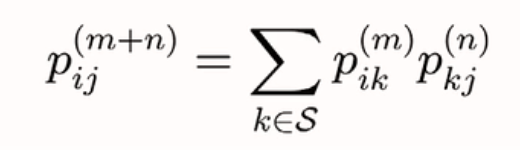
有向图中，节点 i 就是状态 i，边是步长，边权重是概率

节点 i  --x-->节点 j《=》p(1)ij=f(1)ij = 从状态 i 经过1步（首次）到达状态 j 的概率是x 

节点 i  --x-->节点 j --y-->节点 k 《=》f(2)ij = 从 i 经过2步首次到达状态 j 的概率是x*y 

p(n)ij：从 i 经过n步到达 j 的概率，所以它包括首次

pij：从i到达j的概率，是所有可能的步数情况概率之和

f(n)ij：从 i 经过n 首次到 j 的概率 ；

fij：从 i 首次到 j 的概率

可达：

可达满足传递性

a可达b《=》a能（沿着n条有向边）走到b

xy互通《=》x可达y且y可达x《=》x能走向y，y能走向x

 

 

 

 

 互通的状态都属于同一类，不同类的状态不互通

不可约：所有状态互通（该链不可再分解）

状态的周期是回到自己所有可能的步数的最大公约数

非周期《=》周期=1

有自循环的状态周期是1

若回不来周期记为无穷大：

 

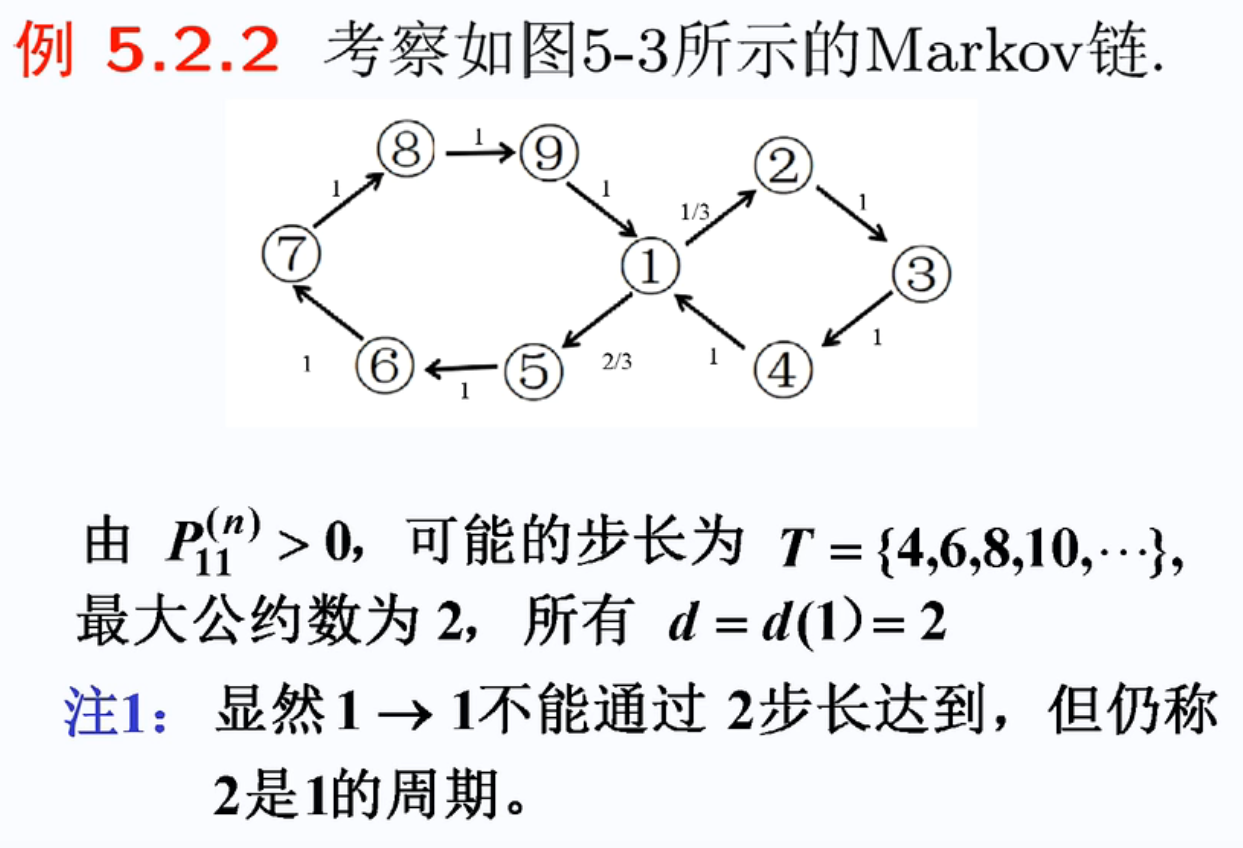
 互通的状态（同一类的状态）周期一致 ，常返性一致（都是常返 / 正常返 / 0常返 / 遍历态 / 都不是）

fij：从 i 首次走到 j  的概率《=》从 i 出发经过有限步骤首次到 j 的概率（中间不经过 j ，即首次，p没有首次）

常返态 i ：从 i 出发一定能走到 i 《=》状态图中一定能回来《=》fii=1

非常返态：状态图中有可能回不来了

 

  常返态的平均返回时间（首次）：

 

状态分类： 

  

 例子（解：先画图，再互通来分类，看周期）：

 

 

 

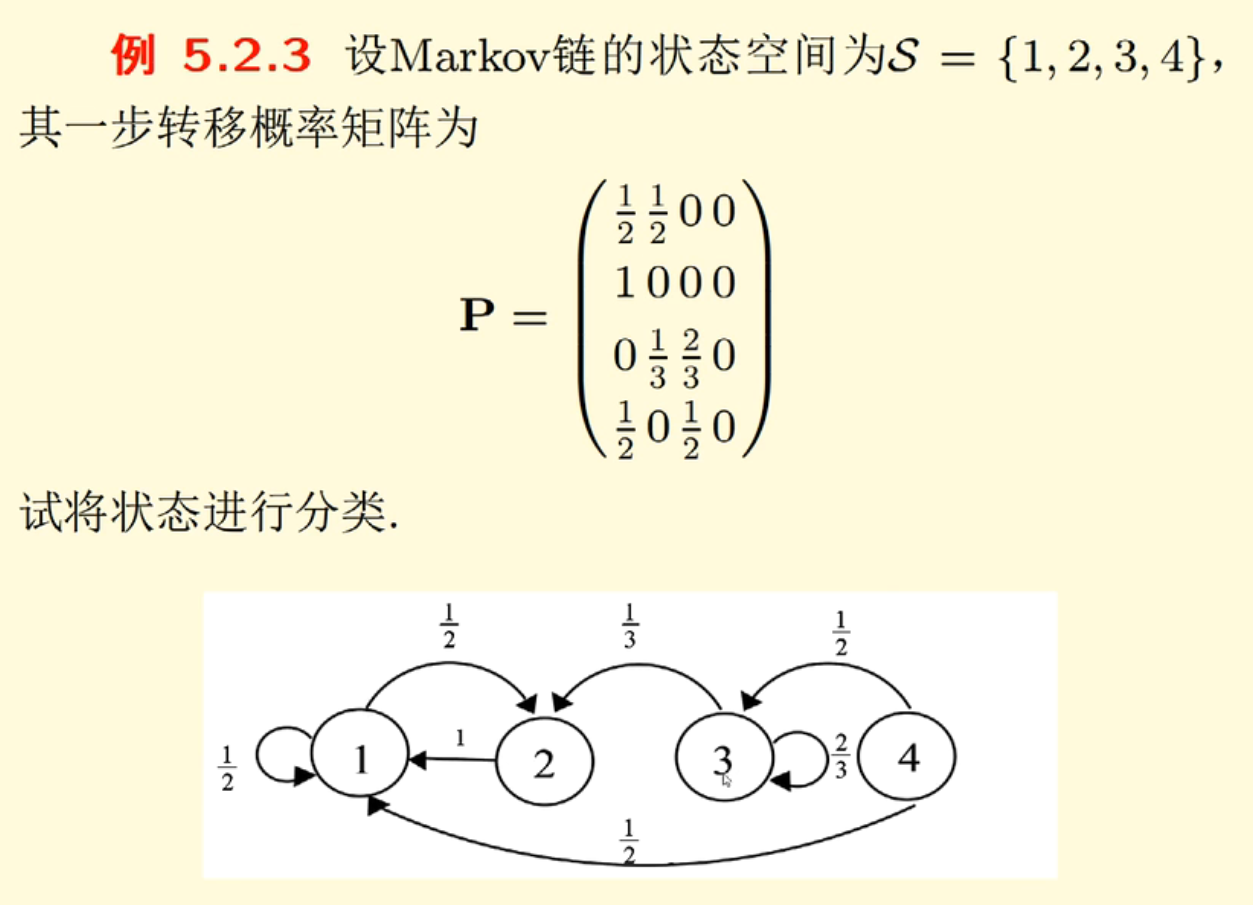
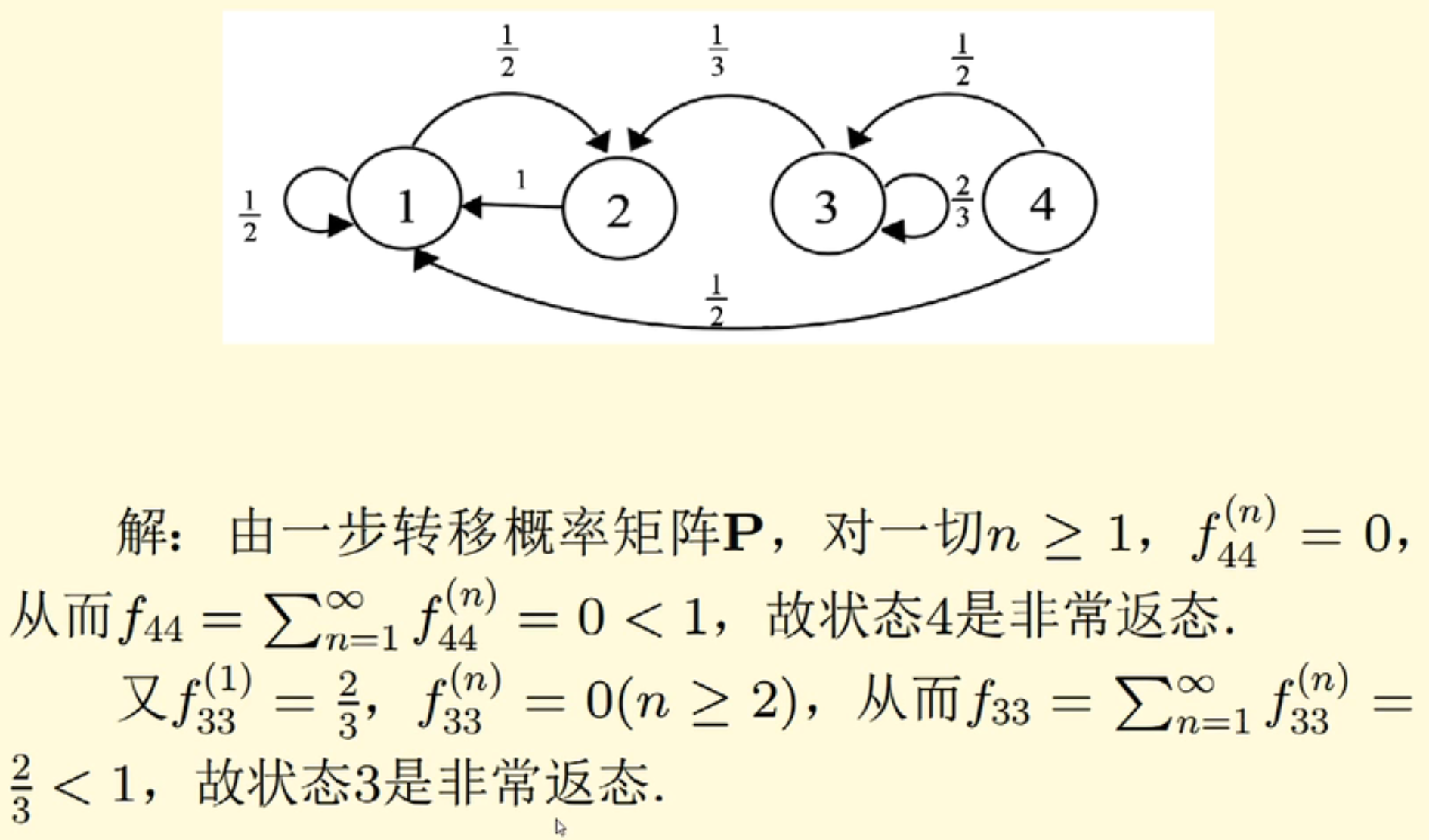
一条路径上的概率相乘是这条路径的概率

 

 

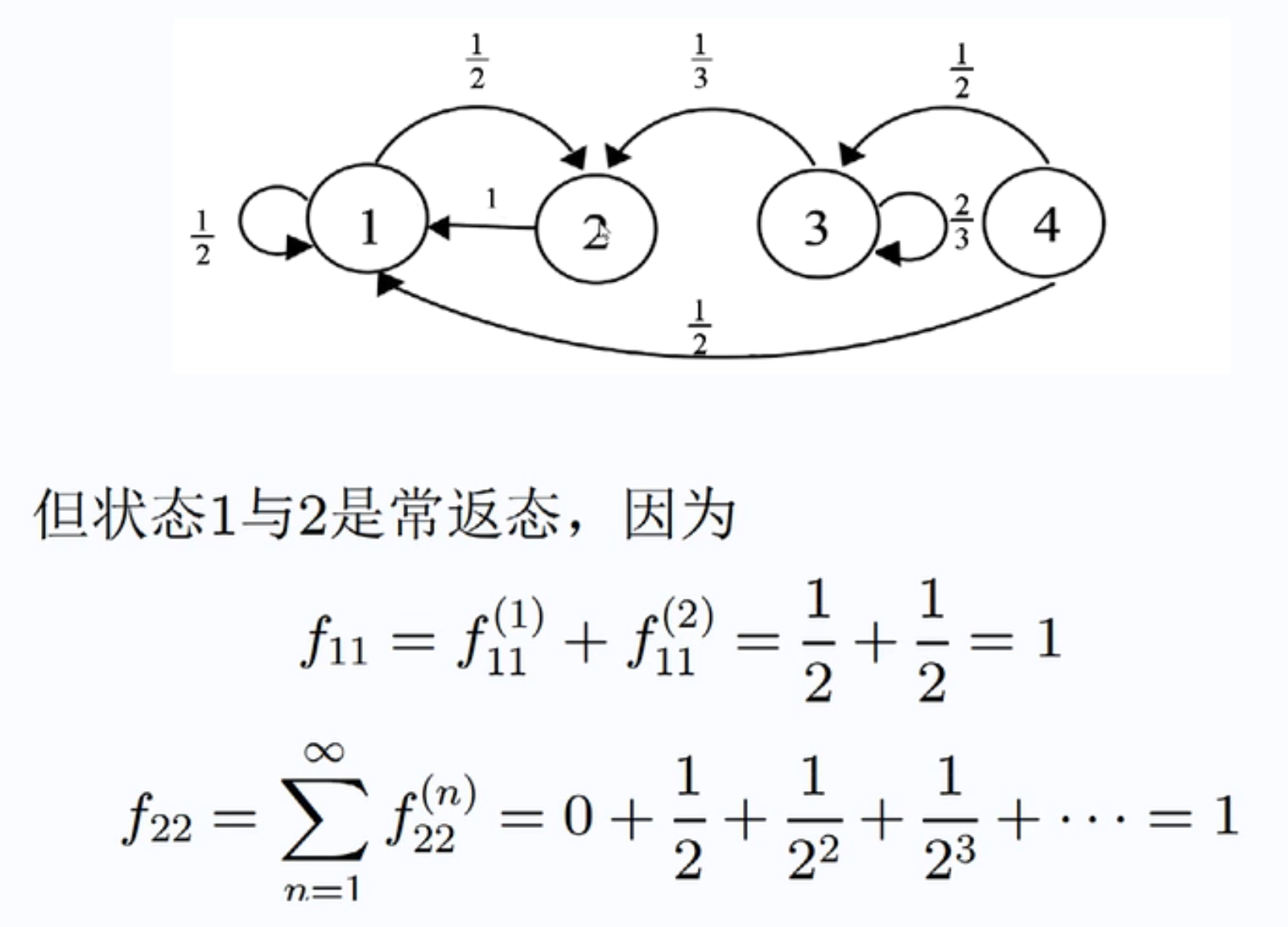
常返态经过无穷步（周期的倍数）转移到自己的概率是确定的，为周期/平均返回时间，即 

 

经过无穷多步不会转移到非常返态以及零常返态了，即

 

 正常返态的互通状态经过无穷多步（nd+r）到正常返态的概率是个确定的数，即

 

 

 

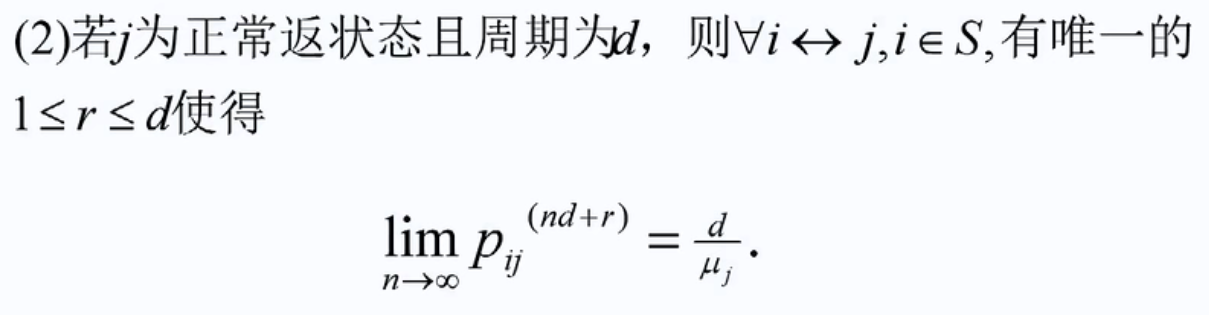
有限状态的马氏链一定有正常返态

 

 zzz

 例子：

 

 平稳分布是个概率向量，每个状态对应其每个概率：

 

  平稳分布定义：

 

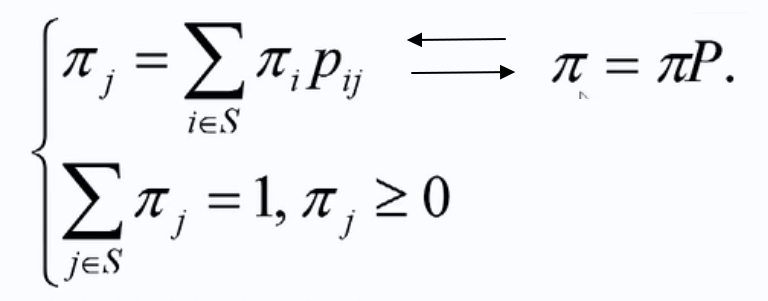
 若状态初始概率符合平稳分布，不管转移多少步，状态概率不变

遍历的马氏链：所有状态相通且都是遍历态

 

遍历的马氏链的极限分布是唯一的平稳分布：

 

 

例子（首先状态有限，状态互通，周期为1=》遍历的马氏链）：

 

 

例子：

 

 

 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

 

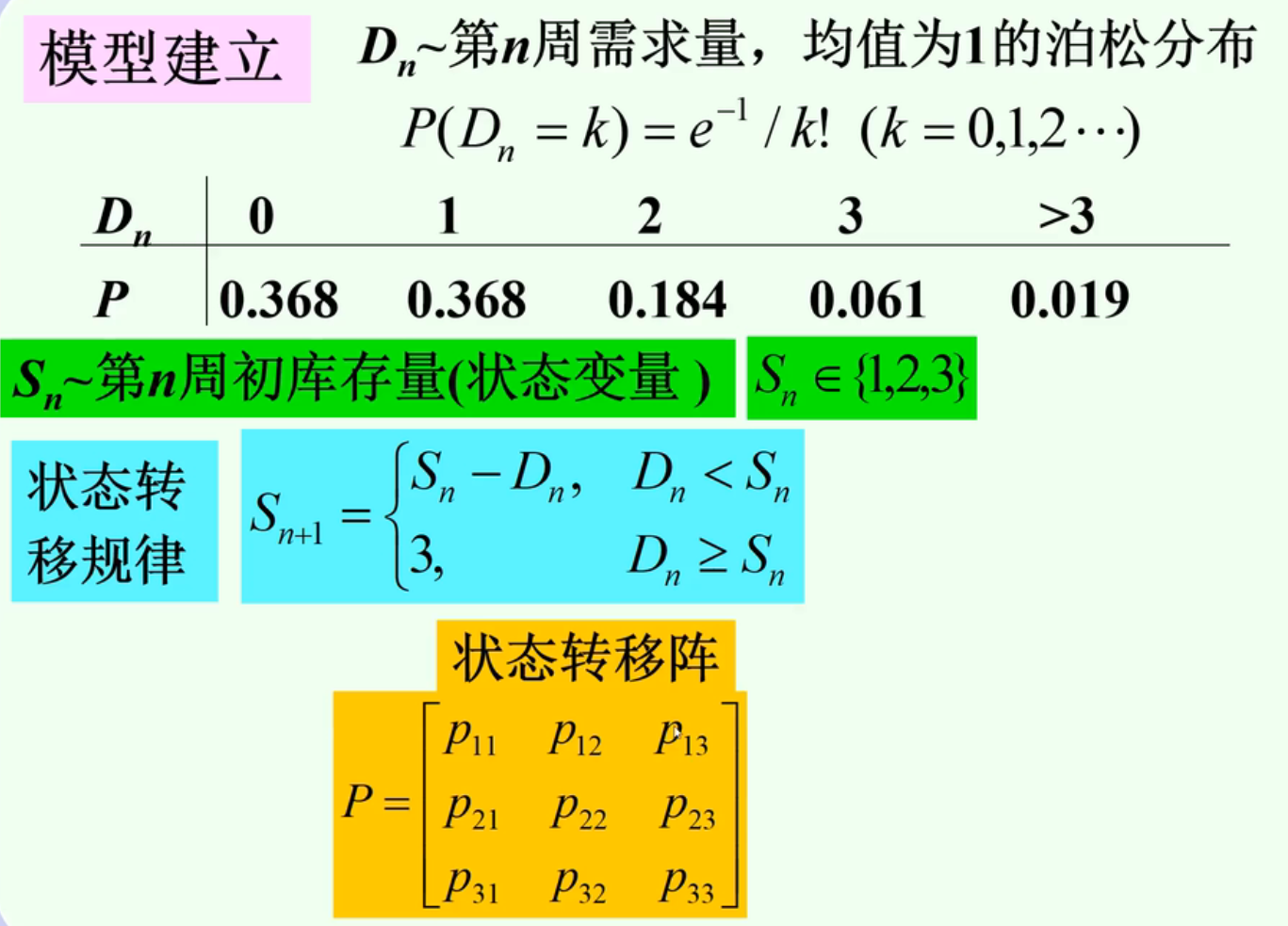
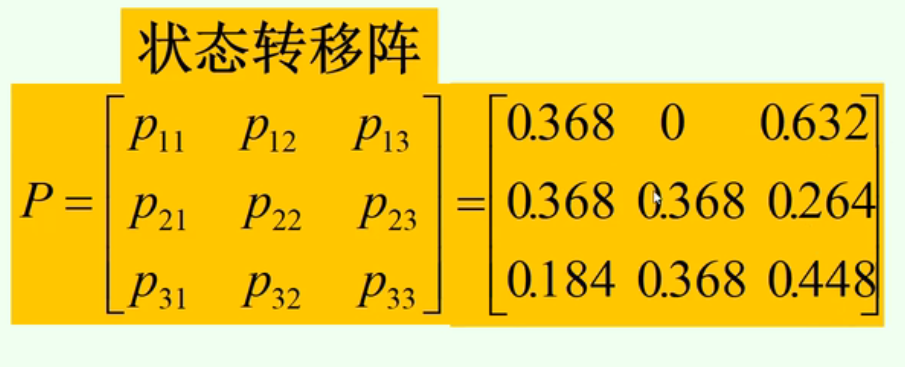
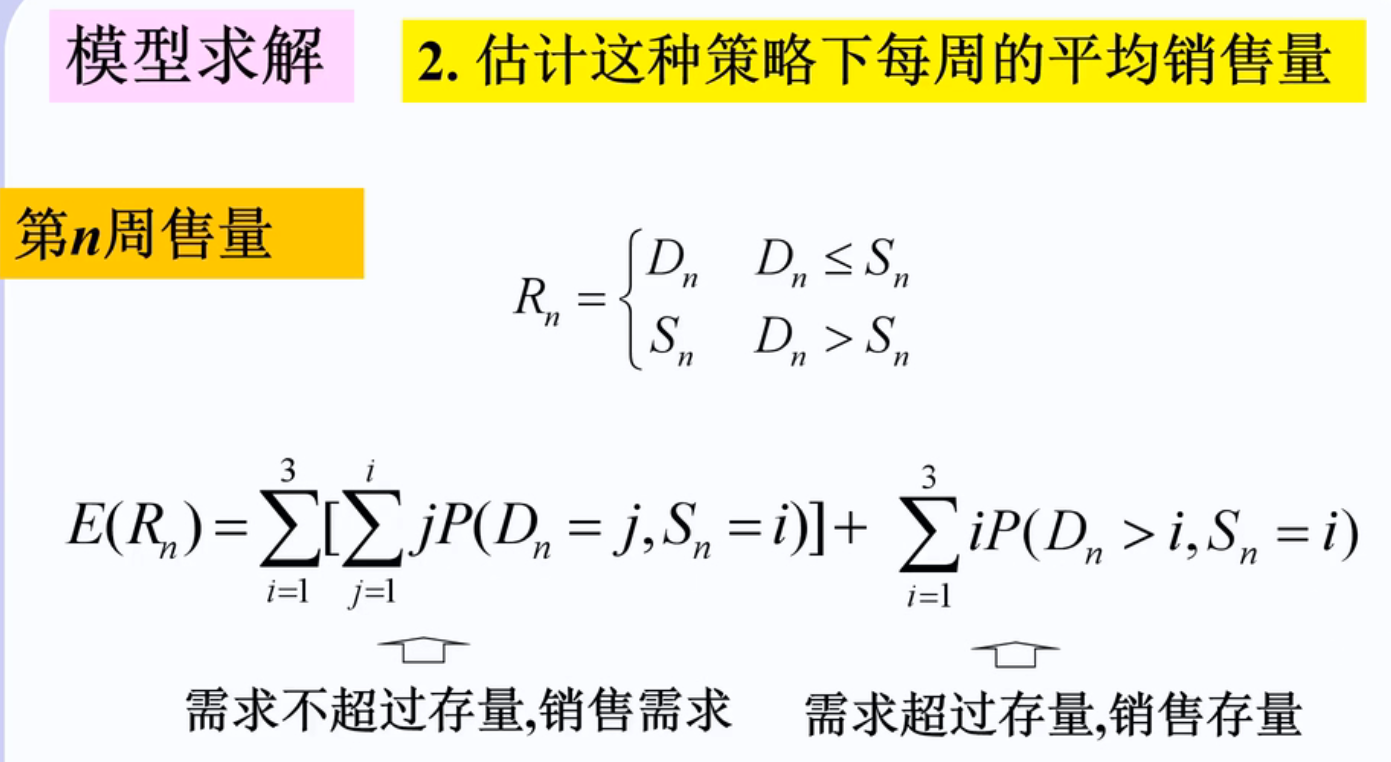
 例子：

 

 

 

 

 

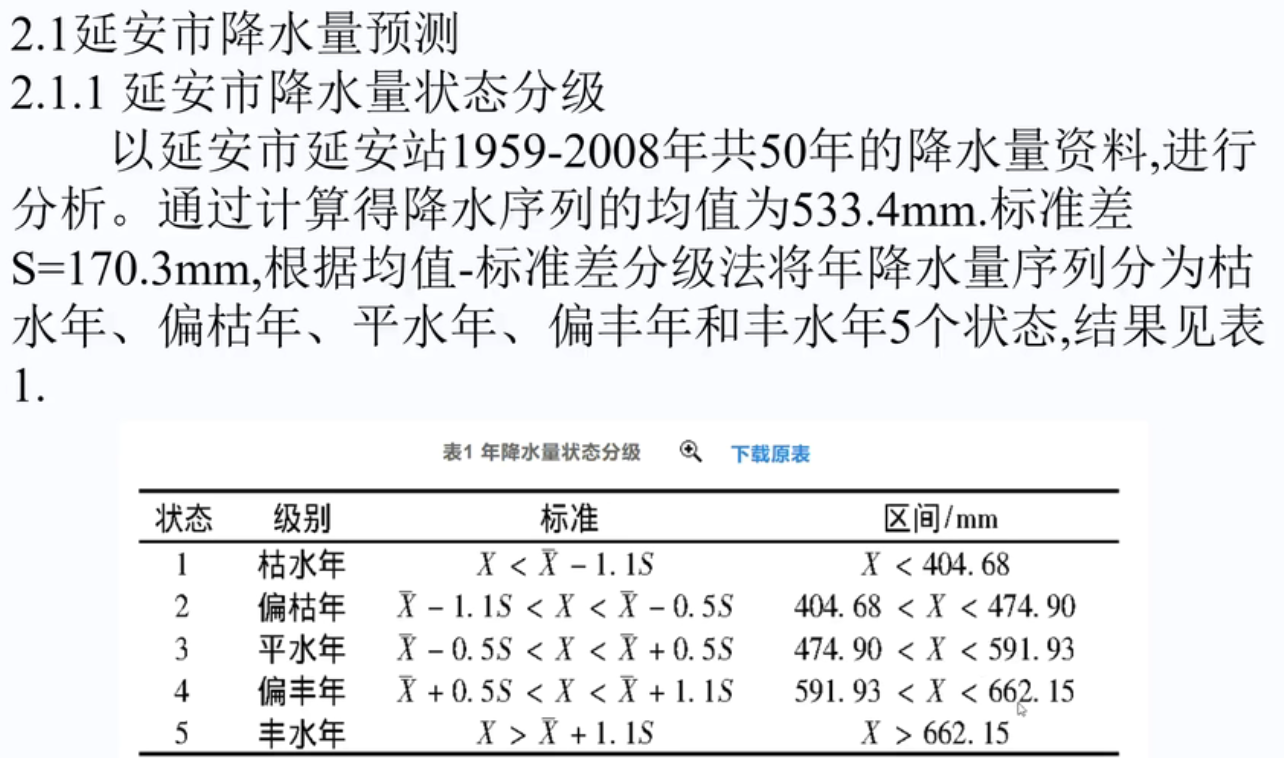
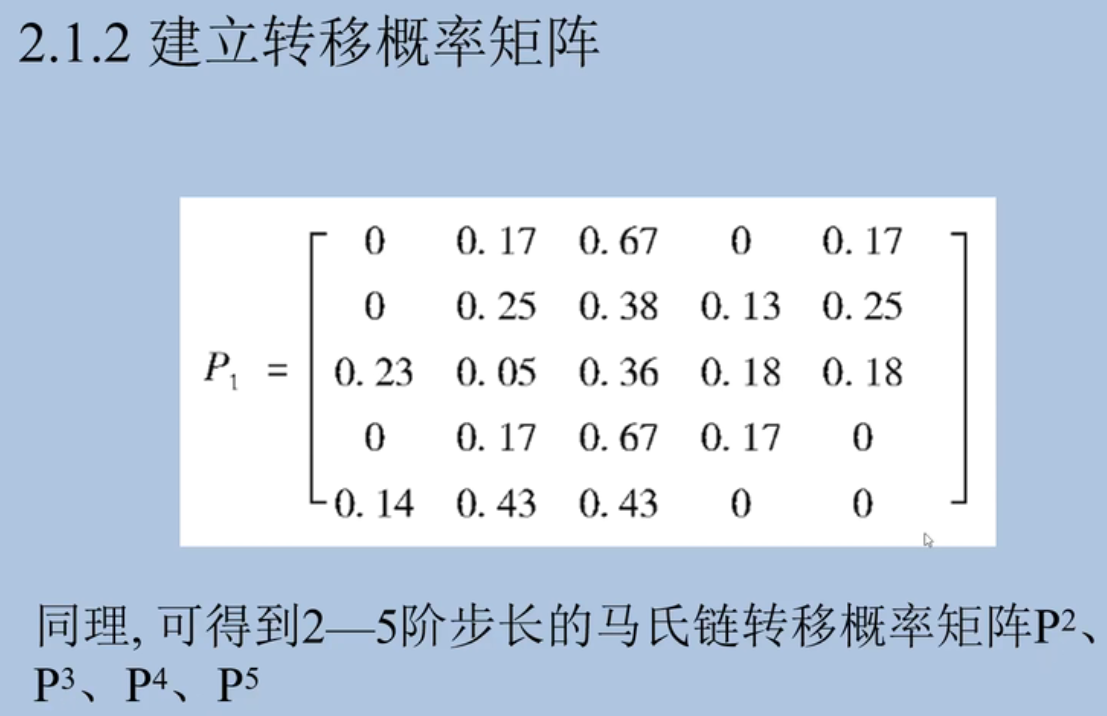
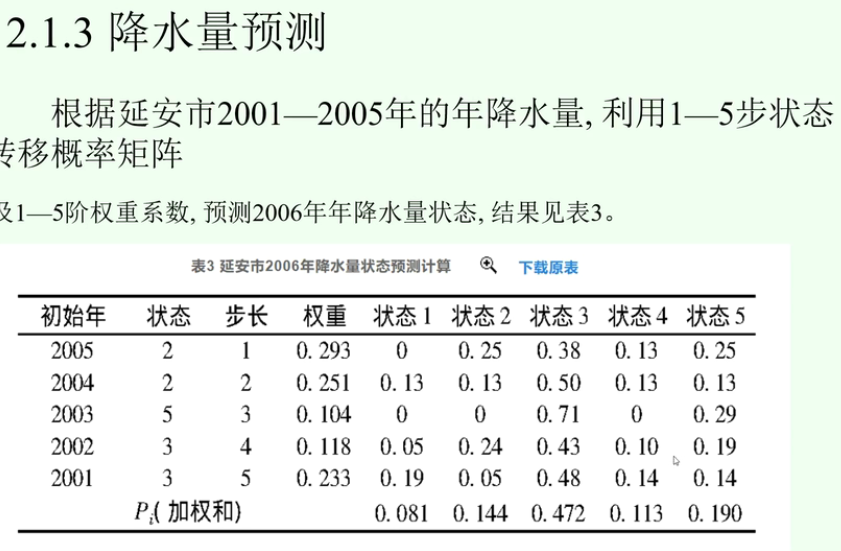
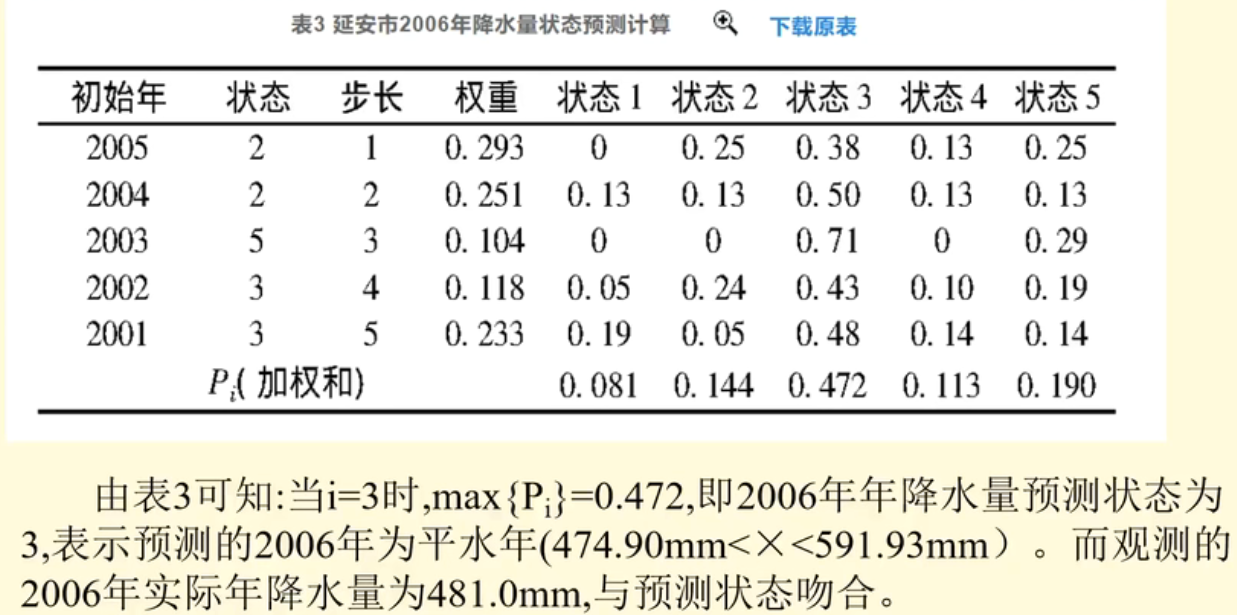
 权重可以通过与06年的相似度计算