cv1
线性代数
逆矩阵:
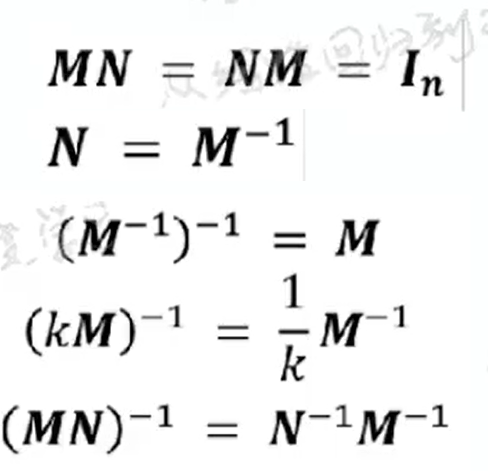
对称:

基:线性无关且能表示出其他任意向量
正交基:22正交的基
任意3个正交的向量构成三维空间的1个正交基
内积=0 <=> 正交
a和单位向量的内积=a在单位向量的投影

标量场U(x,y,z)是数值,形成场的量为向量,称该场为向量场
方向导数是沿着某个方向的变化率,沿着某个方向的导数 ,若>0,则沿该方向函数值增大。
梯度是一个向量,指向函数值增长最快的方向,沿着梯度方向导数最大,且为该点最大方向导数
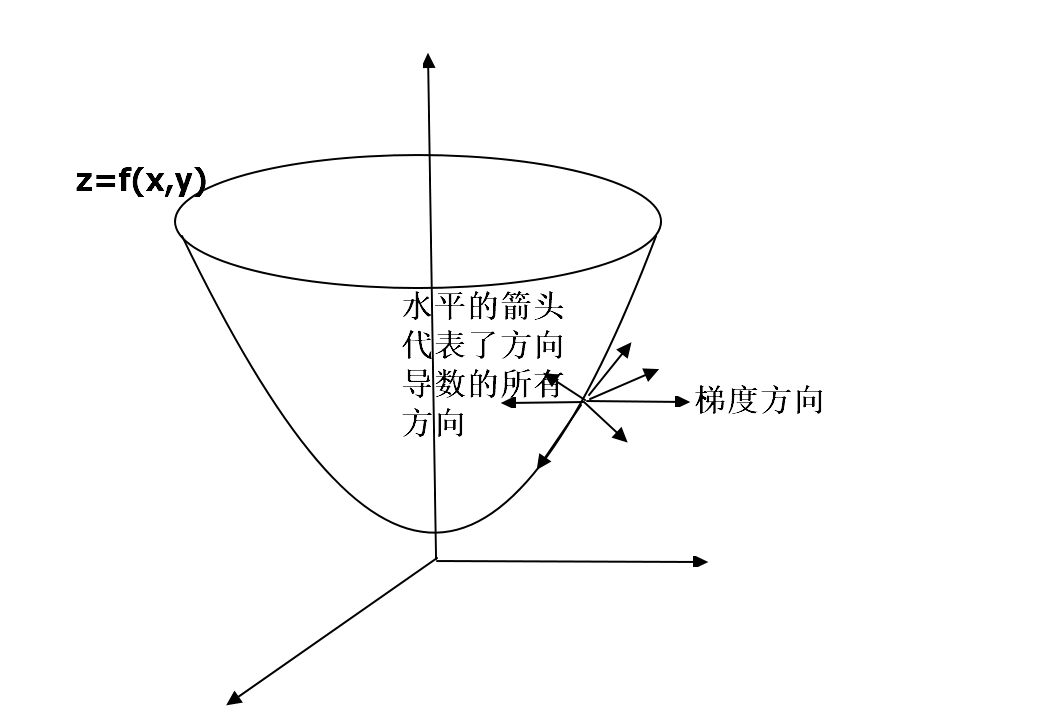
梯度 · 单位方向向量 = 方向导数,grad = ▽

argmax(f(x)):使得f(x)取最大值的x
已知几个点,平面上找到一条直线(或一个单位向量w),使得这些点到直线的距离平方和最小,即投影平方和最大,已知w是未知的单位向量:
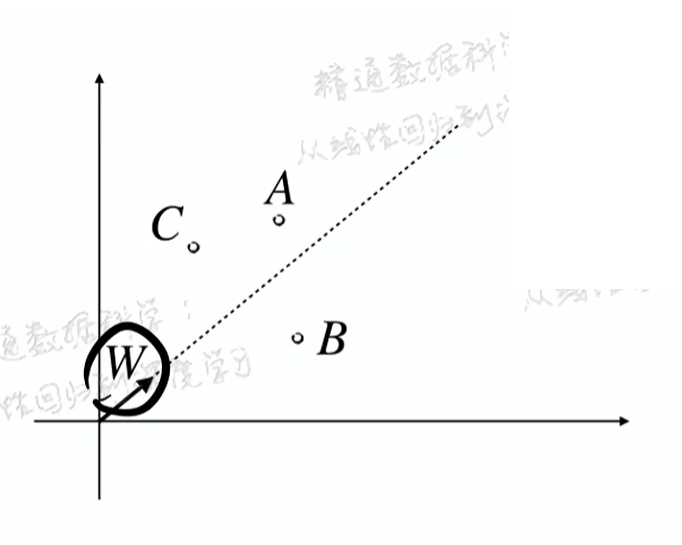
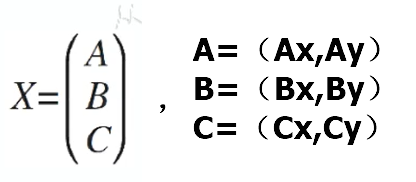
目标函数:
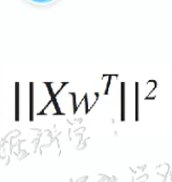
求解目标函数最大时的w是多少,先纪为 v :
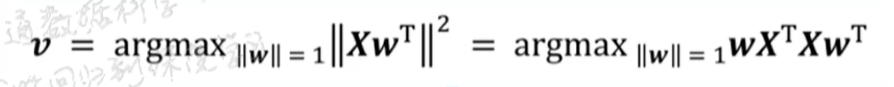
![]()
根据
Av=λv:列向量v是A的一个特征向量,λ是相应的特征值;
n阶矩阵有n个特征值;实对称矩阵的特征值都是实数,且不同特征值对应的特征向量正交
所以答案是:

经典统计学
变量分为定性变量和定量变量,定量变量是数值型的,分为连续型变量和离散型变量;定性变量分为无序变量(无等级的,又分为二项分类,即只有2个取值,多项分类是有多个取值)和有序变量(按照等级不同分类,如坏、一般、好、很好)
要研究广州的男的婴儿的身高:
同质性:都广州的、都男的、都婴儿
异质性:同质性基础上个体的差异,他们的身高
对医生人群(研究总体)抽取一部分医生出来(这些个体构成的一份样本),研究规律,进而推广到更大范围的人群(目标总体)
样本空间=所有基本事件的集合,基本事件=样本点
总体均值就是所有取值的平均值
参数是总体的,如总体均值μ、总体标准差σ,统计量是样本的,如样本均值X把,样本标准差S
统计描述就是描述样本,如频率分布表、直条图
统计推断就是用统计量来估计总体参数
观察性研究=调查研究:是不施加干预的,如吸烟与否和得肺癌的概率;实验研究是施加干预的,如是否接种疫苗的情况下,对某疾病的研究
连续型变量的频率图:


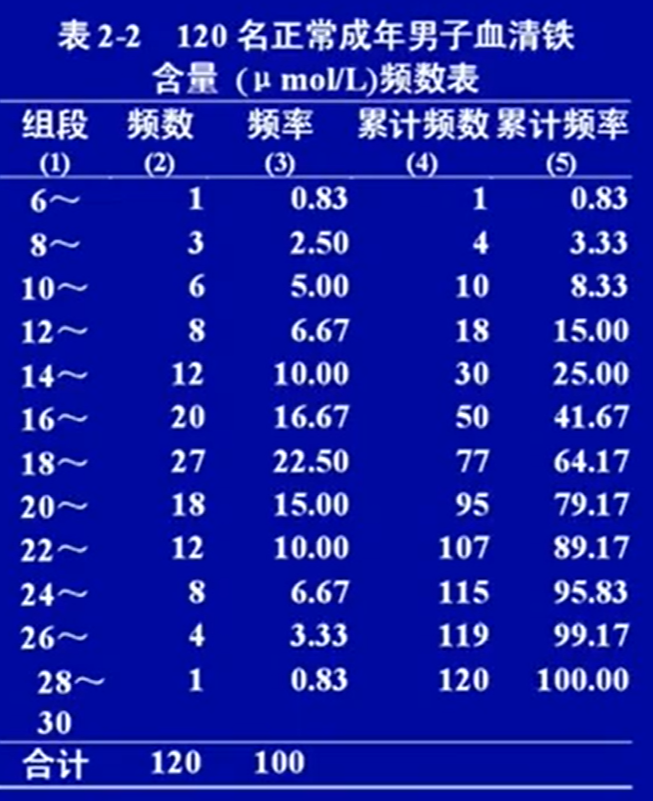
可以直接酸,也可以用加权法计算算术平均,用组中值代替:7*0.83+9*2.5+..
直方图:此时纵轴是频率密度=频率 / 组距
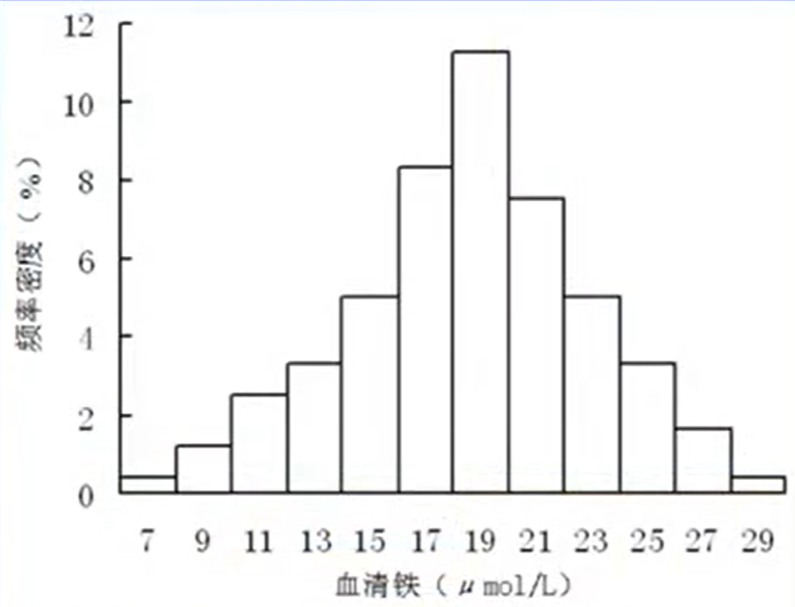
几何均数:
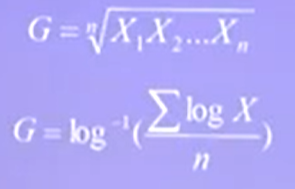
加权法计算几何均数,f 是对应的频数:
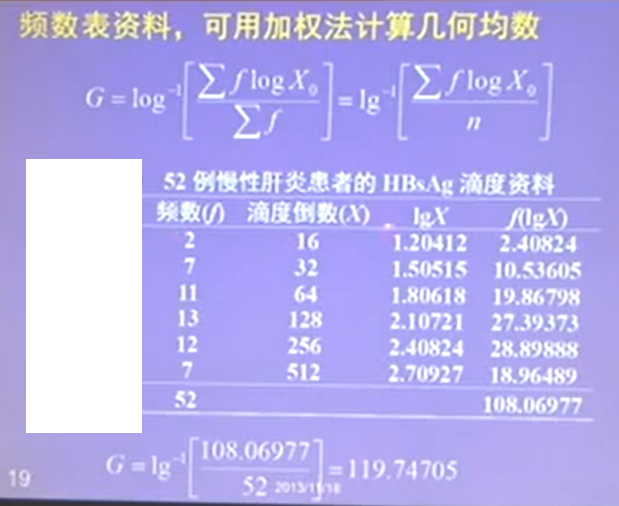
中位数P50,即50%的数比它小(P75:75%比它小):
数据排序后:
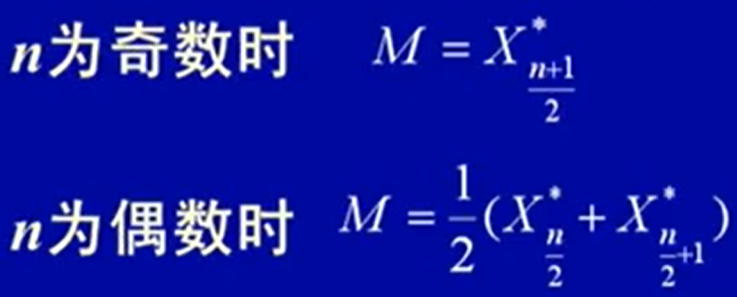
频率分布直方图中,中位数实现了切割,使得左右面积=0.5,即左边的累积频率=0.5
衡量一组数据的变异情况:极差(最大值-最小值,能反映整体覆盖的范围)、四分位数间距(P75-P25,反映了一半的人覆盖的范围)、方差(越大则变异越大)、标准差(方差开根号,为了使得和原变量量纲一致,表示平均一个个体离开均值有多远)、变异系数(可以比较不同组数据的变异,标准差/平均值,消除了量纲)
总体方差:

样本方差:
只要定了n-1个人,且知道均值,就知道最后那个数据了,所以自由度n-1,此处分母就是除以自由度

强度 = 发病人数 / 总共活的时间
下图4个杠代表1年:

频数:n次试验中,事件A发生的次数
排列组合:

概率:


A和B独立 <=> P(AB) = P(A) * P(B)
随机变量的取值是不固定的,但是是有概率规律的,分为离散型和连续型,第一次投色子的值是什么,可以记为X1,第二次X2
二项分布:

期望与方差分别为:np、np(1-p)

均值(做了n次实验,该事件平均发生的次数)和方差:

泊松分布用于描述罕见事件发生的次数:
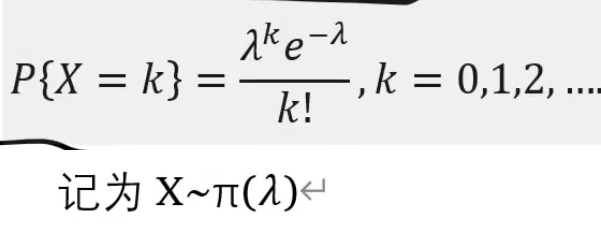
均值=方差 =λ
服从泊松分布的相互独立的随机变量之和也服从泊松分布

3个分布关系:
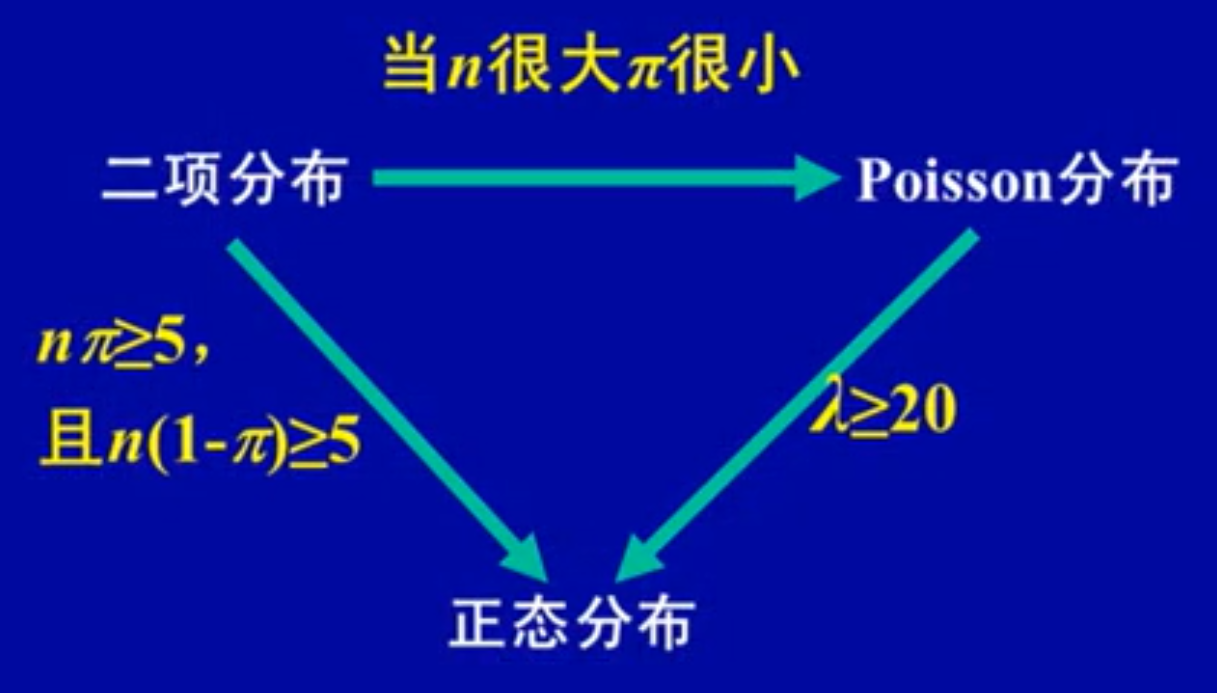
分布函数 = 概率密度的积分:
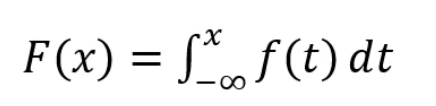
均匀分布:
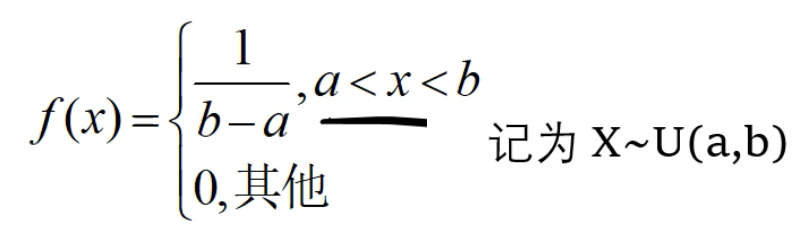
指数分布:
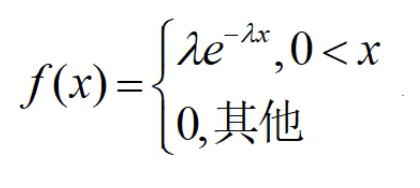
正态分布,μ是中心位置,方差越大,越矮胖:
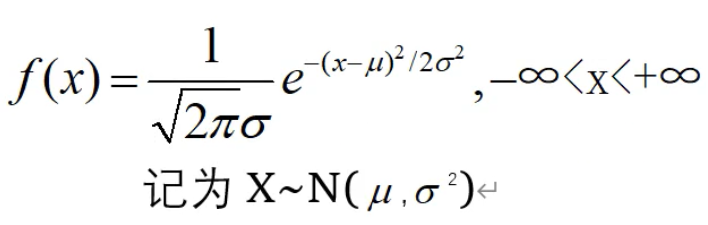
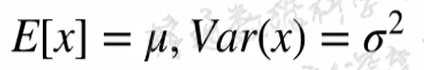
Z变换:
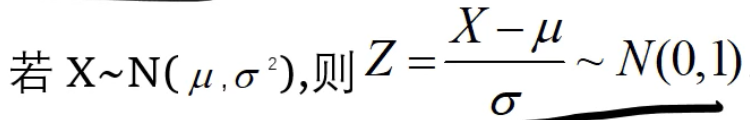
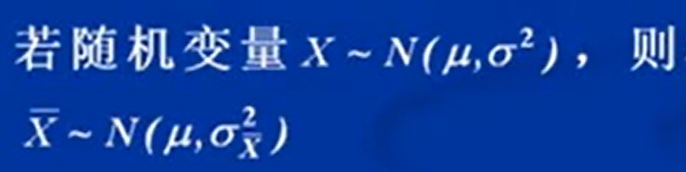
正态分布中,μ+σ是曲线拐点
正态分布常用区间:
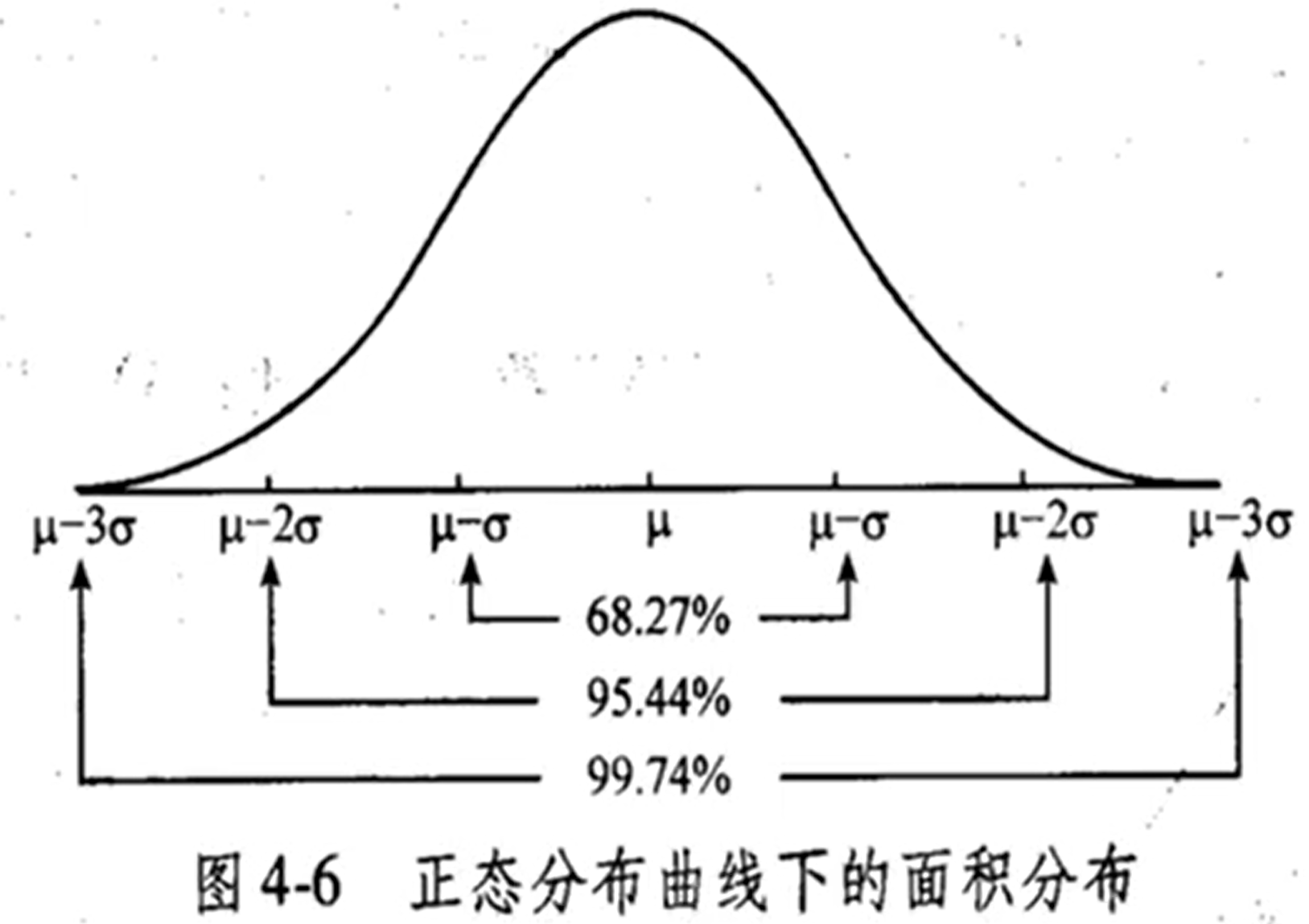

Zα:标准正态分布的上α分位点:
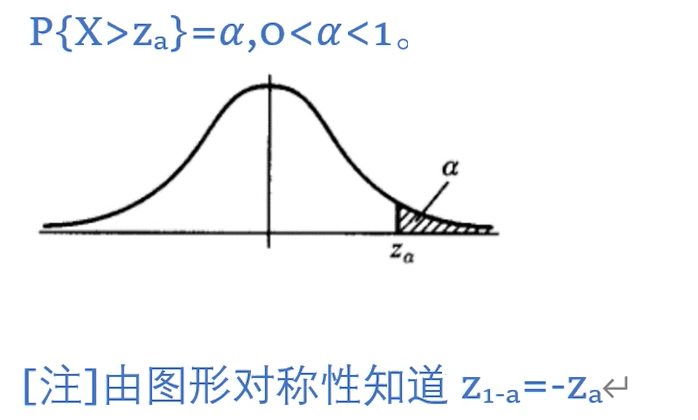
分布函数:
![]()
连续型分布函数 = 概率密度函数左边的积分

y = acsinx:
连续型随机变量函数例题:

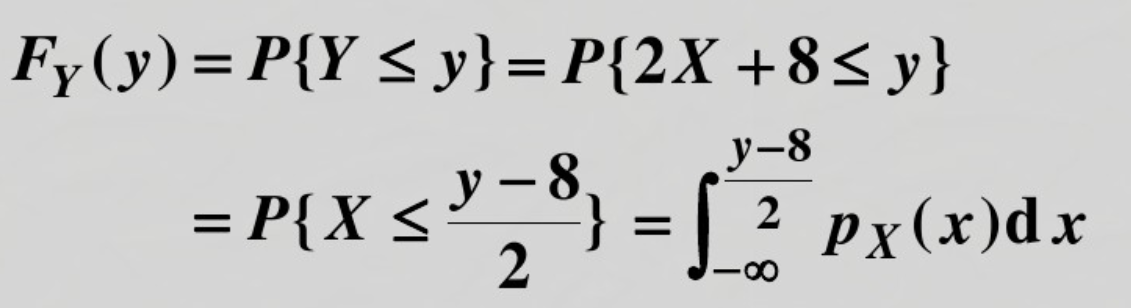

二维随机变量(X,Y):
![]()
连续性二维随机变量:
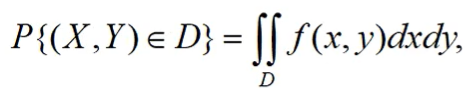
边缘分布:

条件分布:
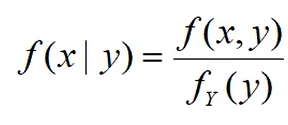
X和Y独立 < == >
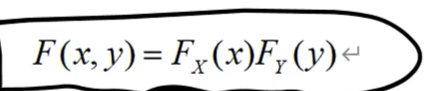
<==>
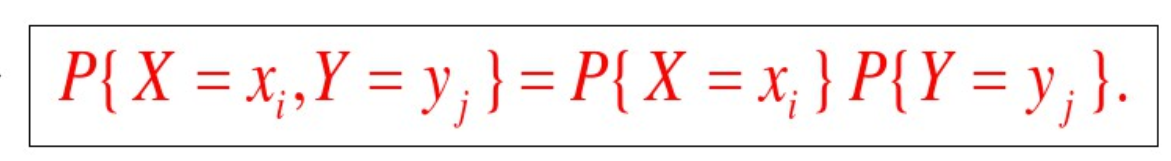
<==>
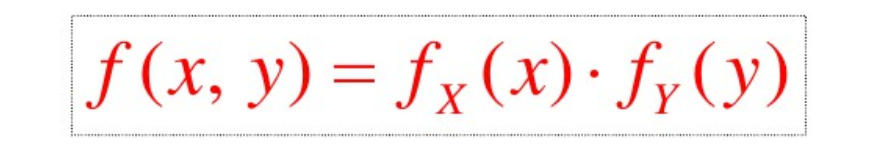
对于二维正态随机变量(X,Y),X与Y独立<==> ρ=0
数学期望:
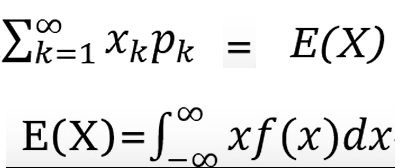
方差:
![]()
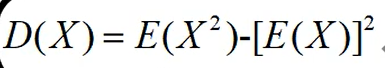
相关系数:
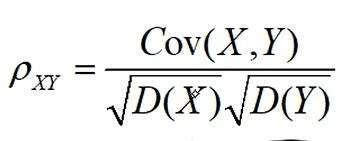
相关系数=0 <=> 不相关
协方差:
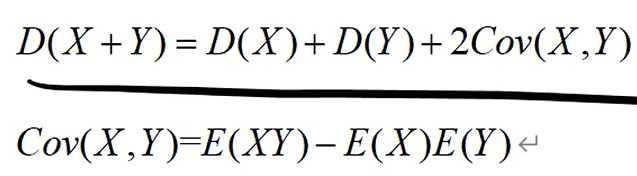
中心极限定理(样本量足够大时,样本均值的分布近似正态分布):
一堆随机变量独立同分布,则
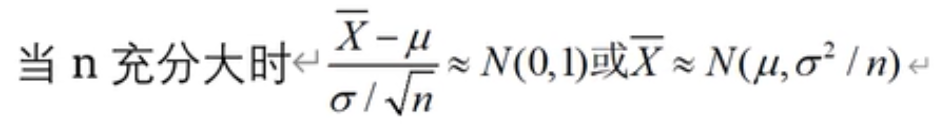
一堆随机变量独立同分布,则
当n充分大时,随机变量之和服从正态分布
X~正态分布 => aX+b 服从正态分布
(简单随机)样本里面的随机变量们(X1,X2...)独立同分布IID,且都与总体同分布
频率 = 频数 / 总数
频率直方图中第一步是扩大区间形成的x轴范围用来包括所有数据:

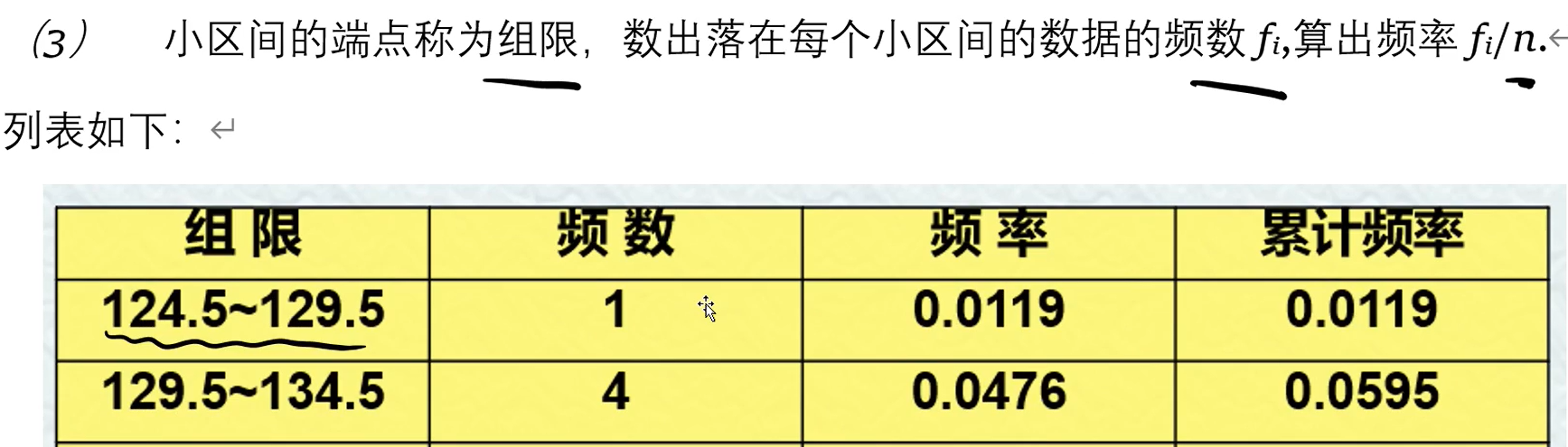
频率直方图总面积=1
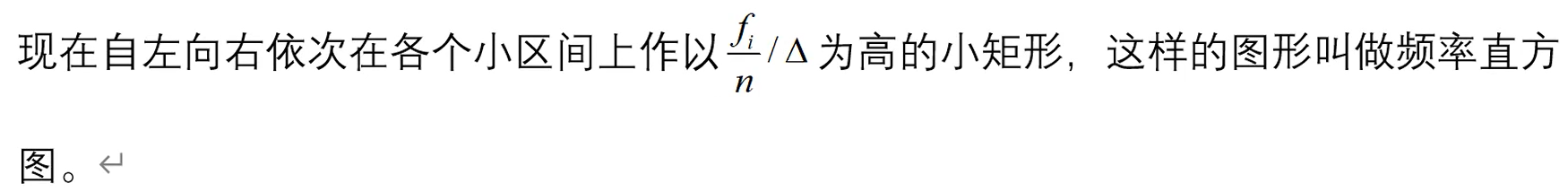
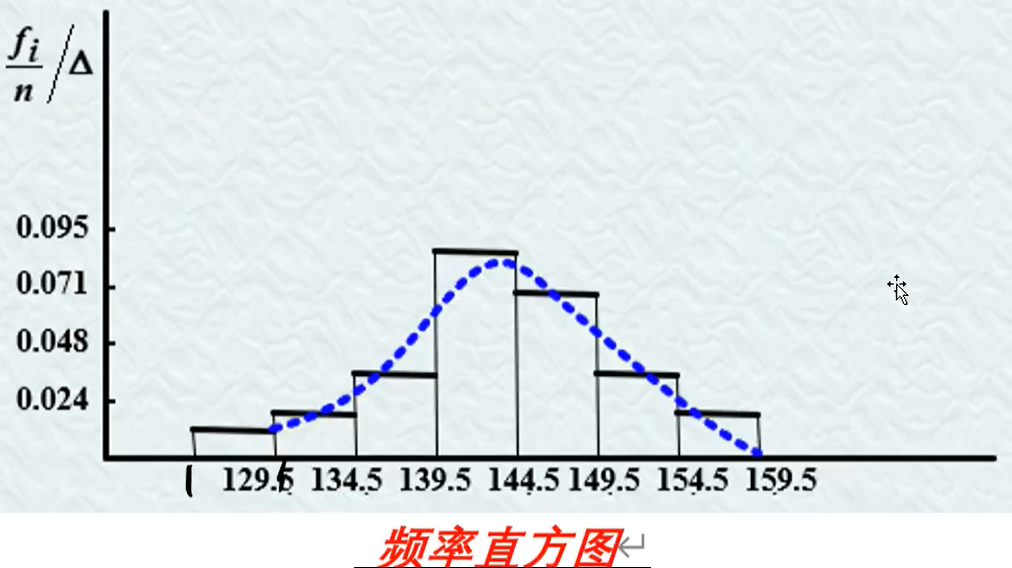
统计量是样本的函数,是一堆随机变量的函数,不含有未知参数:g(X1,X2,X3...)
下面都是统计量:
样本均值:
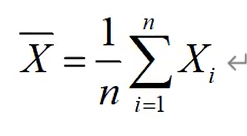
样本方差:

样本标准差:
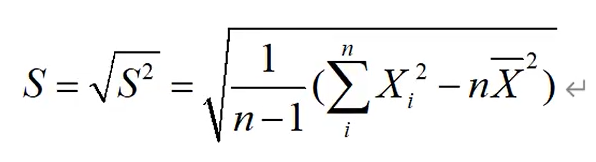

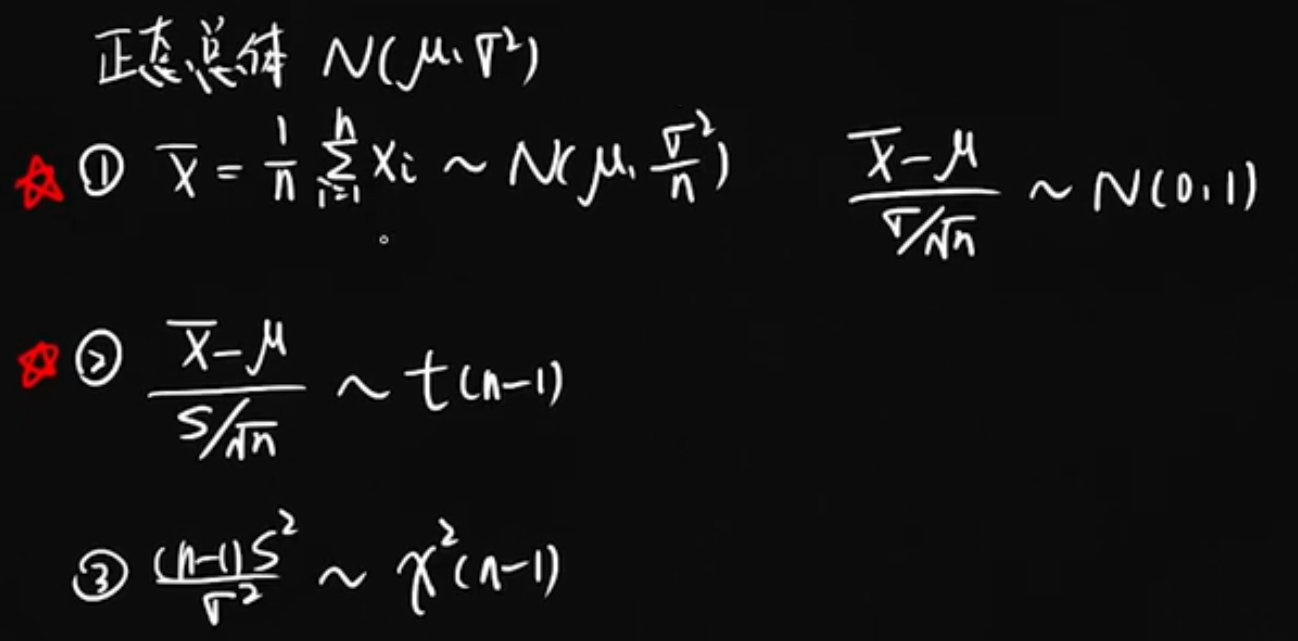
对数公式:
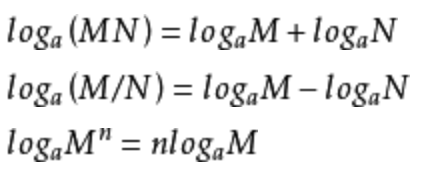
统计推断包括参数估计和假设检验
一个样本含有多个个体,抽样误差指的是样本均值之间存在的误差,用标准误(样本均值的标准差=X把的标准差=根号下X把的方差)来表示抽样误差的大小
样本均数的均数=总体均值,而标准误(n是样本量,样本内的个体数,X把对应的分母):
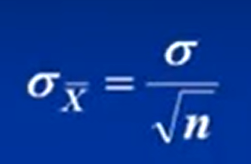
t分布:
X服从正态分布,则:

性质:

点估计:根据样本估计总体参数的一个值
似然函数L = 样本的概率密度函数 = f(x1)f(x2)f(x3)....f(xn),如果总体有未知参数Θ,它的最大似然估计量= 使L取最大值的Θ(已知结果求原因),此时自变量只有Θ,X1...Xn都是常数

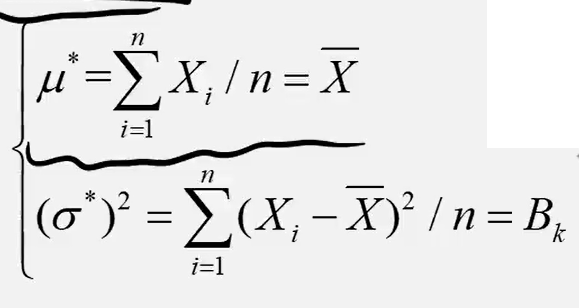
离散样本的似然函数 = P(X1=x1,X2=x2...Xn=xn)
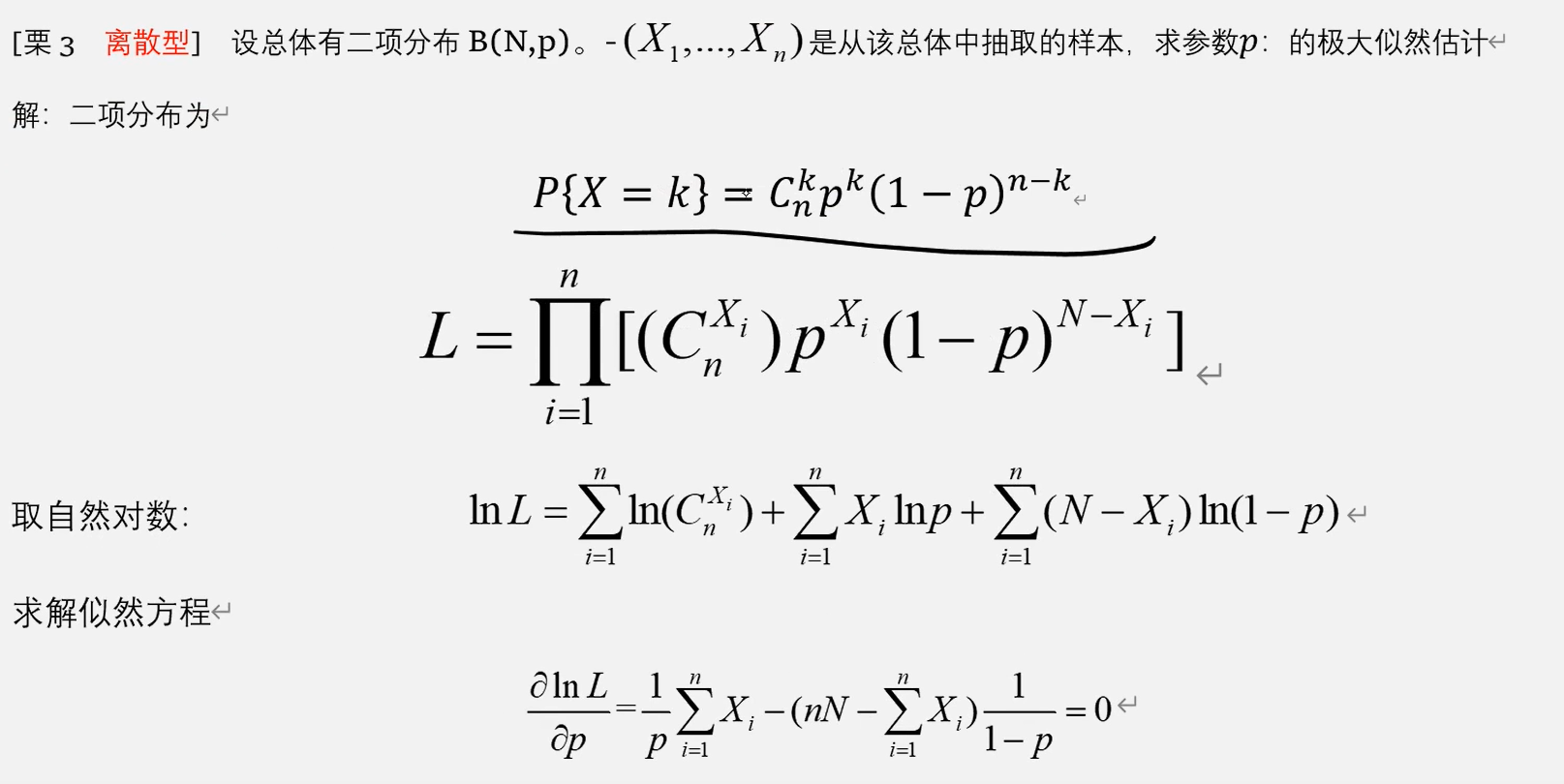
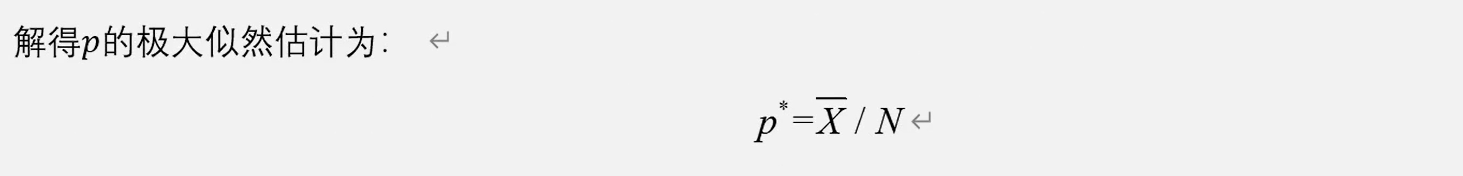
区间估计:根据样本估计总体参数所在的区间,不同的样本构造的区间不一定一样,该区间为置信区间,左端点=置信上限,右端点=置信下限
P(θ >θ_) >= 1-α 《=》(θ_ , +oo)是θ的单侧置信区间,置信度是1-α,θ_ 是单侧置信下限
置信区间(a,b),显著性水平α,置信度=置信水平=1-α
《=》置信区间(a,b)包含真实值的概率是1-α
例题:方差已知,估计总体均值,总体正态分布,显著性水平为0.05
解:
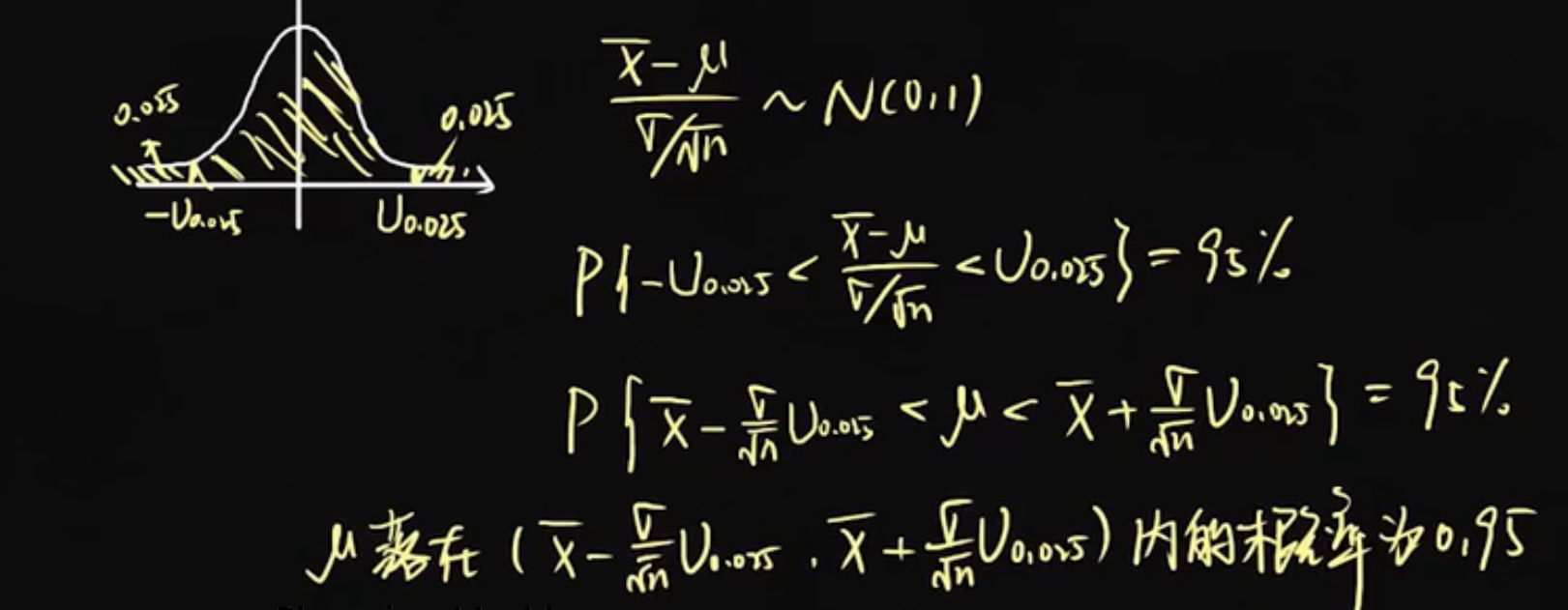
结论:
方差已知,估计总体均值,总体正态分布,显著性水平为α,则:
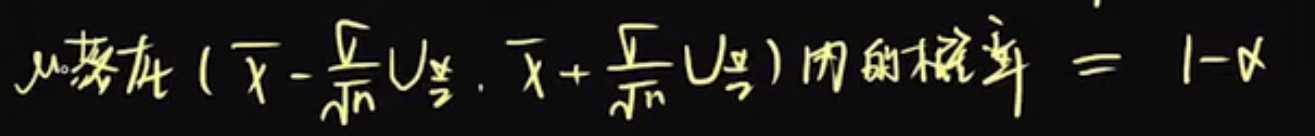
总结(正态是前提):

例题:

二项分布当n很大时,X趋于正态分布N(np,npq)
假设检验
对总体做个假设,然后根据样本看看要不要拒绝这个假设
通常在使用假设检验=显著性检验时,会将希望证明的结论或者新的事件作为备择假设(H1)。因为通过数据拒绝原假设可以有较强的说服力证明备择假设。
例题:


假设检验中的错误:
显著性检验是仅控制犯第一类错误的概率,犯第一类错误的概率为显著性水平α,样本容量固定时,任何一类错误概率减小,另一类必然增大;要想两者概率都降低,只能增大样本容量

单个正态总体下:
(算出统计量的取值,如果它在拒绝域,则拒绝H0,否则接受)
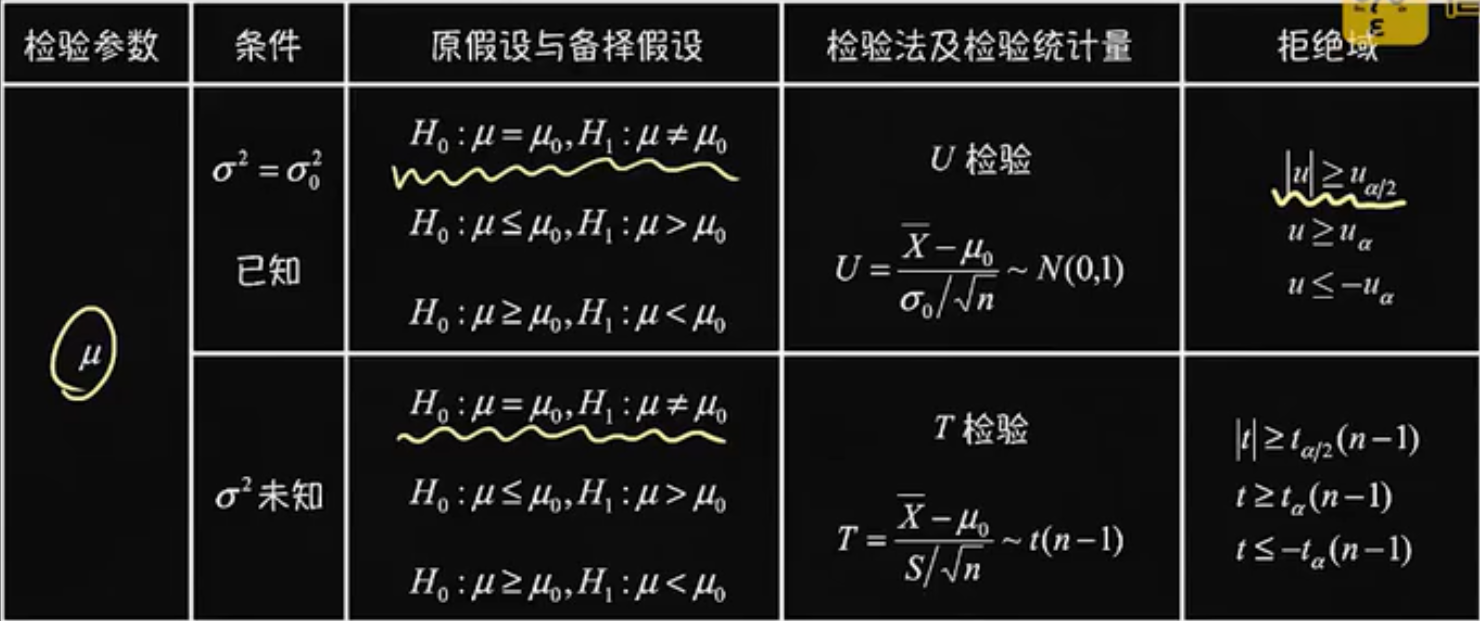
拒绝或者接受H0的另一个方法是P值,P值是概率,是概率函数曲线下的面积,是反对原假设的强度,p值越小,越能充分地拒绝H0
若H0的形式是=,则算出统计量的取值a后,想象曲线上横坐标的a,计算统计量在两边的面积就是 p
若H0的形式是<=,则算出统计量的取值a后,想象曲线上横坐标的a,计算 P(统计量>=a) 或者在a右边曲线下的面积= p
若H0的形式是>=,则算出统计量的取值a后,想象曲线上横坐标的a,计算 P(统计量<=a) 或者在a左边曲线下的面积= p
再给一个α,若α >= p ,则在显著性水平α下拒绝H0,α大于的越多,拒绝的把握性越大,小于则接受原假设。(注意P值得计算不依赖与α)

统计学假设数据是独立同分布的,假设空间包含了所有要尝试的模型
若有标签,则称监督学习,否则是非监督学习。
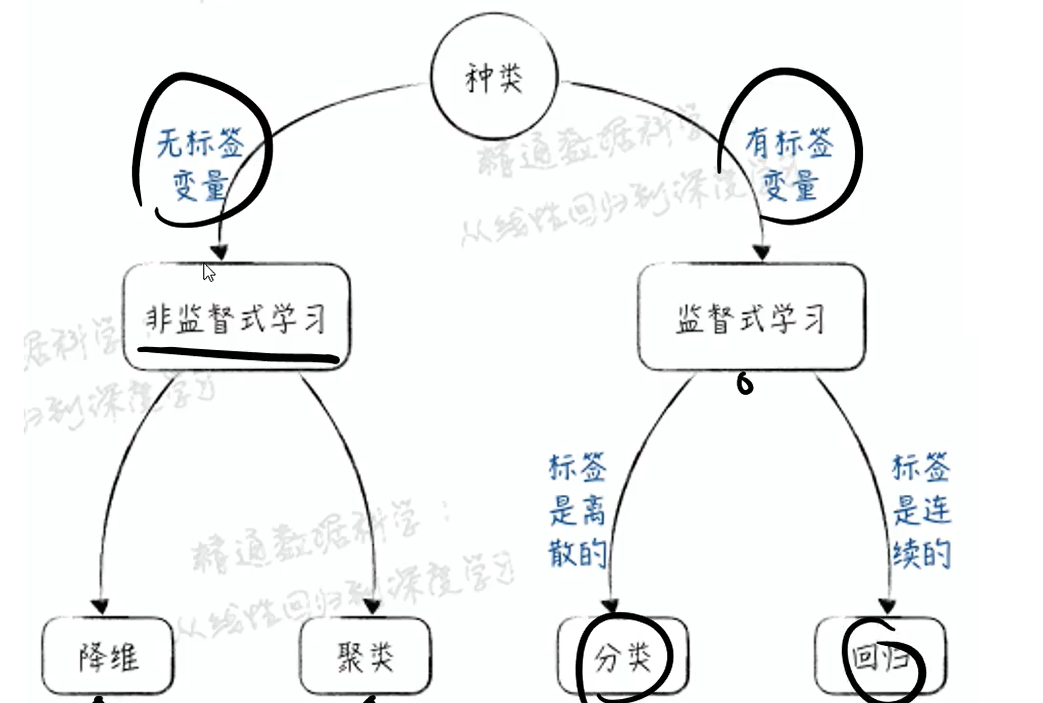
所有特征向量所在的空间:特征空间
约定:
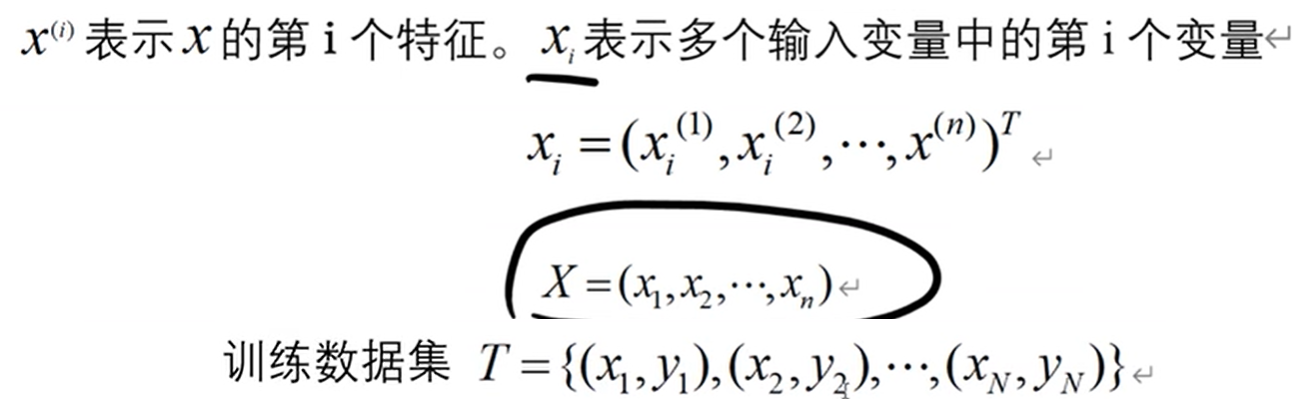
样本点:输入和输出对
监督学习假定输入X和输出Y遵循概率分布;假设空间包含一堆模型;监督学习的模型满足P(Y|X)或Y= f (X)
f(AB) = f(A|B) f(B) = f(B|A) f(A)
贝叶斯统计学
贝叶斯统计学使用到了先验信息(之前的资料或者经验),认为未知参数θ不是常亮,而是随机的,先验分布为:θ~π(θ),此时x和θ是有联合概率密度的 f (x,θ)
思想:利用先验分布,结合样本,求出后验分布,然后用后验分布来推断
π(θ) 就是θ的概率密度函数 ,H(θ)是它的分布函数,m(x) 是只有x的概率密度函数
后验分布H(θ|x)的概率密度函数是π(θ|x)
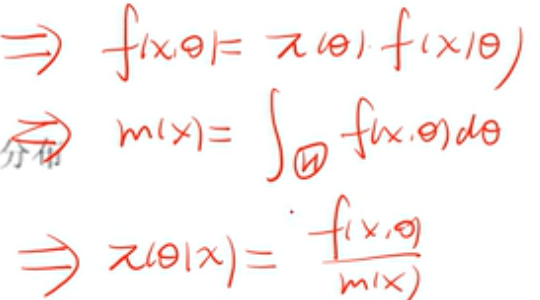
当B1,B2,B3瓦解了S(22不交,并集=S):
![]()

无信息先验:若参数空间有限,则θ去每个值得概率是1/n;若参数空间是个区间,则服从均匀分布;若参数空间无界,则采用广义先验密度
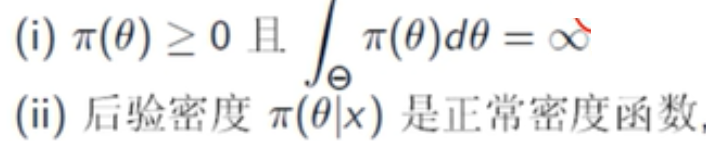
下题中,π(θ|x)是以θ位变量的,所有分母不用算,根据正比形式看出是正态,直接写出答案

共轭先验分布簇中任意取一个分布,其后验分布还属于该簇
伽玛函数:

贝塔函数(P,Q>0):
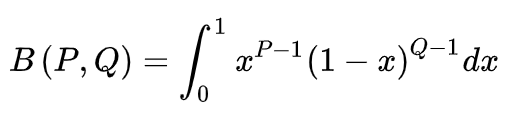
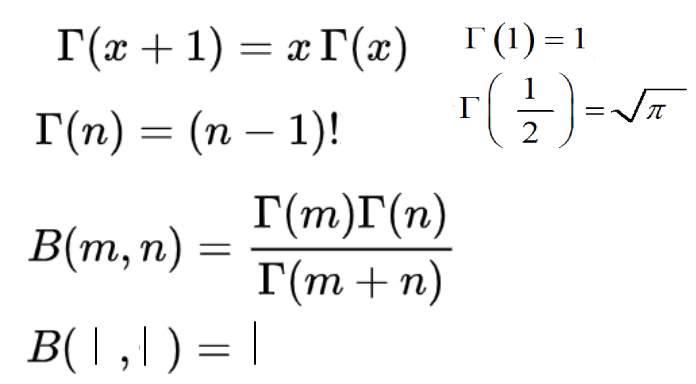
伽马分布X~Gamma(α,β)的密度函数、期望、方差:
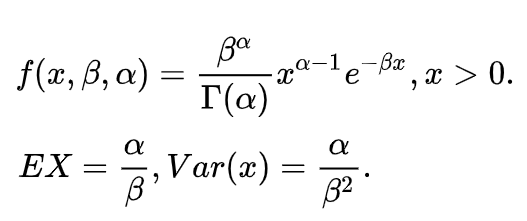
贝塔分布定义在(0,1)
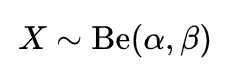
《=》
概率密度函数是:
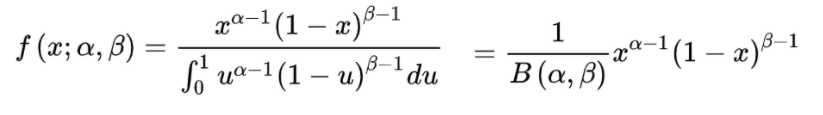
贝塔分布期望值和方差分别是:
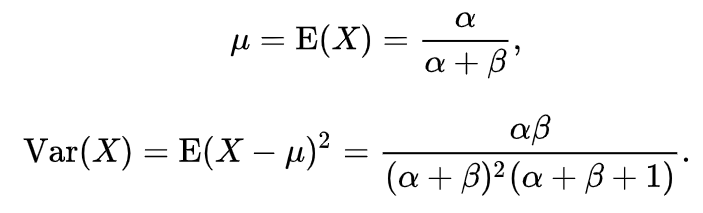
X~Be(1,1)=U(0,1)
感知器:y = f(w·x+b),w是权重向量,x是输入向量,b是偏置,f是激活函数
设计一个感知器,让它来实现and运算。下面是它的真值表: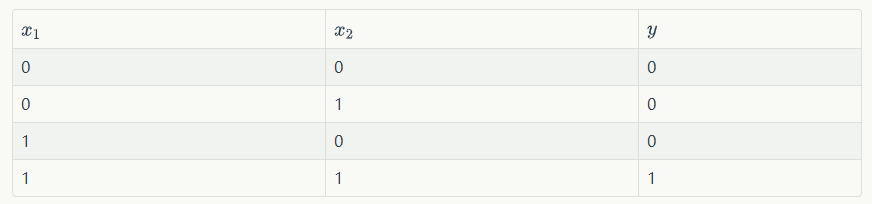
设计:令w1=0.5,w2=0.5,b=-0.8,而激活函数是阶跃函数:
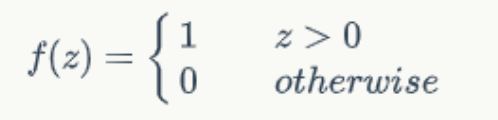
输入真值表第一行,即x1=x2=0,则输出为:
即当x1=x2=0时,y=0,这是真值表的第一行。
傅里叶变换:
周期函数=无数个正弦波的叠加,不同频率的正弦波=频率分量
三角函数:周期T=2π/ω;角频率=ω;频率f= 1/T= ω/2π;wx+t:相位;t:初相位
p(t)=90+20sin(160πt),其中振幅A=20,最小正周期T=2π/(160π)=1/80,频率f=1/T=80
频谱=频域图像中,x轴是频率,y轴是该频率信号的幅度
电视频道:不同的频道就是将不同的频率作为一个通道来进行信息传输。
滤波:从某条曲线中去除一些特定的频率成分
相位差=时间差/周期*2π




