力扣2
21搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例 1:
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1
解答:
public int search(int[] nums, int target) { int low = 0; int high = nums.length-1; int mid; // 45 0123 // 单个数也算 while (low<=high){ // 先看中间是不是目标值,不是再分 mid = (low+high)/2; if(nums[mid]==target){ return mid; } // 如果[low,mid]是递增数列(包含1个数的) if(nums[low]<=nums[mid]){ // 如果目标位于递增数列里面 if(nums[low] <=target && nums[mid]>target ){ high=mid-1; }else{ low = mid+1; } // 如果右边是递增数列 }else { // 如果位于递增数列里面 if(target > nums[mid] && target<=nums[high]){ low = mid+1; }else { high = mid-1; } } } return -1; }
由于二分法的时间复杂度是O(logn),所以可以考虑二分法
给定数组都满足一个模式:2个递增数组挨着
如果采用二分法,分后的2个数组是一个完全递增(本质上也满足原来模式),另一个满足原来模式
若目标落在递增数组(最左边的数<最右边的数)里面,则在递增数组里面讨论,继续原来方法
反之,在另外那个数组(最左边的数>最右边的数)里面讨论,按照原来方法
由于每次的步骤一致,则递归也行
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]
解:
public int[] searchRange(int[] nums, int target) { int[] re = new int[2]; re[0] =-1; re[1] =-1; // 3 4 6 7 7 7 7 7 7 7 7 10 int low=0; int high =nums.length-1; int mid; while (low<=high){ mid = (low+high)/2; // 左指针跑到最左边,右指针跑到最右边 if(nums[mid]==target){ int start = mid; while(mid>0 && nums[mid-1]==target){ mid--; } re[0]=mid; mid =start; while (mid<nums.length-1 && nums[mid+1]==target){ mid++; } re[1]=mid; return re; } if(nums[mid]>target){ high=mid-1; }else{ low=mid+1; } } return re; }
由题意,依然采用二分法
例如:1 4 5 6 6 6 6 6 6 6 6 6 6 10,目标值:6
算出mid后,若刚好碰见目标6,则指针移到最左边确定start,移到最右边确定end
若碰不见,则按往常缩小范围
23 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
示例 1:
输入:candidates =[2,3,6,7],target =7, 所求解集为: [ [7], [2,2,3] ]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
提示:
1 <= candidates.length <= 301 <= candidates[i] <= 200candidate中的每个元素都是独一无二的。1 <= target <= 500
解:
public List<List<Integer>> combinationSum(int[] candidates, int target) { List<List<Integer>> re = new ArrayList<>(); Stack<Integer> stack = new Stack<>(); combine(re,stack,0,candidates,target); return re; } public void combine(List<List<Integer>> re,Stack<Integer> stack,int index,int[] candidates, int target){ if(target==0){ re.add(new ArrayList<>(stack)); } if(target<0){ return; } // stack保存当前答案 for(int i=index;i<candidates.length;i++){ stack.push(candidates[i]); combine(re,stack,i,candidates,target-candidates[i]); stack.pop(); } }
字符串到数字:String str = "1234"; int a = Integer.valueOf(str).intValue();
例如对于:arr:2 3 6 7,target=7,可以有答案:2,2,3;7;...
在答案当中,若以2打头的答案全部找完,则为了不重复,找以3打头的答案时不考虑2;找以4打头的答案时不考虑2,3...
以循环递归方式实现回溯法,以当前正在造的答案作为参数
对于又添加又删除的当前答案,可以使用StringBuffer和栈
24接雨水

解:
public int trap(int[] height) { int n =height.length; if(n<3){ return 0; } int []leftMax = new int[n]; int []rightMax = new int[n]; int sum = 0; // 初始化 leftMax[1] = height[0]; rightMax[n-2] =height[n-1]; for(int i=2;i<n-1;i++){ leftMax[i] = Math.max(leftMax[i-1],height[i-1]); } for(int i=n-3;i>0;i--){ rightMax[i] =Math.max(rightMax[i+1],height[i+1]); } for (int i=1;i<n-1;i++){ int t = Math.min(leftMax[i],rightMax[i]) - height[i]; // 中间的柱子高度必须是最小的 if(t>0){ sum+=t; } } return sum; }
从整体到局部,所有雨水=每个柱子上的雨水之和,其中最左边和最右边的柱子上 不能有雨水
对于中间第 i 个柱子上的雨水 = min(它左边所有柱子的最大值,它右边所有柱子的最大值) - 第 i 个柱子的高度,其中要求第 i 个柱子必须是三者当中的最小的
先算出2个数组,第一个数组是:每个柱子左边的最大值,第二个数组是右边
计算第一个数组时,left [ i ] = max( left[ i-1 ],height[ i ];第二个数组同理
然后再累加,此时两个数组的东西顺手拈来,而且只在乎第 1 到第 n-2 的位置元素
25全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
解:
public List<List<Integer>> permute(int[] nums) { List<List<Integer>> res = new ArrayList<>(); Stack<Integer> stack = new Stack<>(); boolean[] used = new boolean[nums.length]; trace(nums,res,used,stack); return res; } public void trace(int[] nums,List<List<Integer>> res,boolean[] used,Stack<Integer> stack){ // 如果used全是true,说明数字用完了,则add进去,然后return boolean flag =true; for(int i=-0;i<used.length;i++){ flag = flag && used[i]; } if(flag){ res.add(new ArrayList<>(stack)); return; } for (int i=0;i<nums.length;i++){ if(used[i]){ continue; } stack.push(nums[i]); used[i]=true; trace(nums,res,used,stack); stack.pop(); used[i]=false; } }
依然采用回溯,实现方式为循环递归
对递归函数做语义任务:已知当前状态,把所有符合条件的答案放到集合中
for的语义:去找数组中没有用过的数,此时需要一个布尔数组表明有没有用过
递归函数的当前状态为:找到了几个数了,当前集合是什么,哪些数被用过了
26旋转图像
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix = [ [1,2,3], [4,5,6], [7,8,9] ], 原地旋转输入矩阵,使其变为: [ [7,4,1], [8,5,2], [9,6,3] ]
示例 2:
给定 matrix = [ [ 5, 1, 9,11], [ 2, 4, 8,10], [13, 3, 6, 7], [15,14,12,16] ], 原地旋转输入矩阵,使其变为: [ [15,13, 2, 5], [14, 3, 4, 1], [12, 6, 8, 9], [16, 7,10,11] ]
解:
public void rotate(int[][] matrix) { int n = matrix.length; // 对于n*n,只要讨论n/2个框 for(int i=0;i<n/2;i++){ // 对于第i个框,它的边长为 n-2i,每次循环转动4个数,总共循环 n-2i-1次 for(int add=0;add<n-2*i-1;add++){ int t=matrix[i][i+add]; matrix[i][i+add] = matrix[n-i-1-add][i]; matrix[n-i-1-add][i]=matrix[n-i-1][n-i-1-add]; matrix[n-i-1][n-i-1-add] = matrix[i+add][n-i-1]; matrix[i+add][n-i-1] = t; } } }
由于旋转一个框不会影响到别的元素,把旋转矩阵的整体分解成旋转一个一个的正方形框: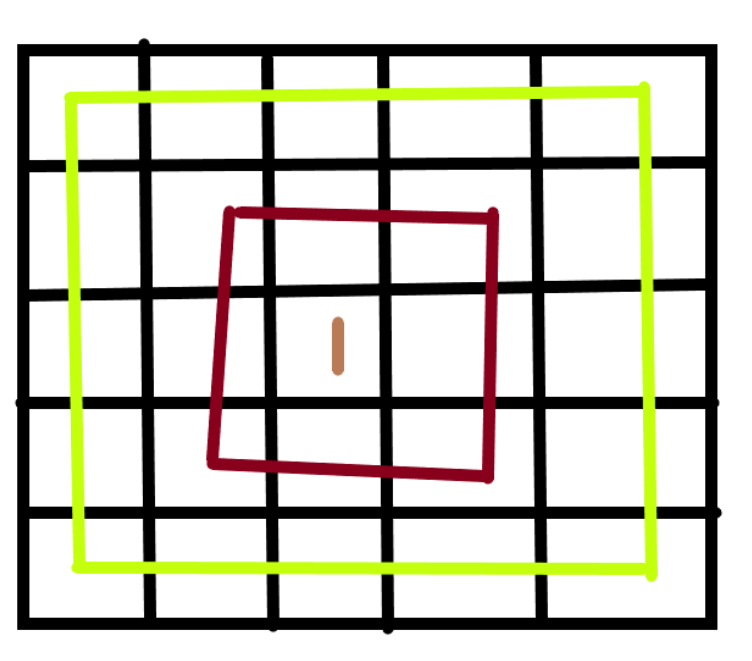
在旋转n*n大小的框时,由于旋转对称的四个点不会影响到别人,则再缩小为每次旋转4个点,直到把这个框上的点旋转完。
旋转4个点可以统一化处理,第一次的四个点中add=0,随后add=1,add=2:
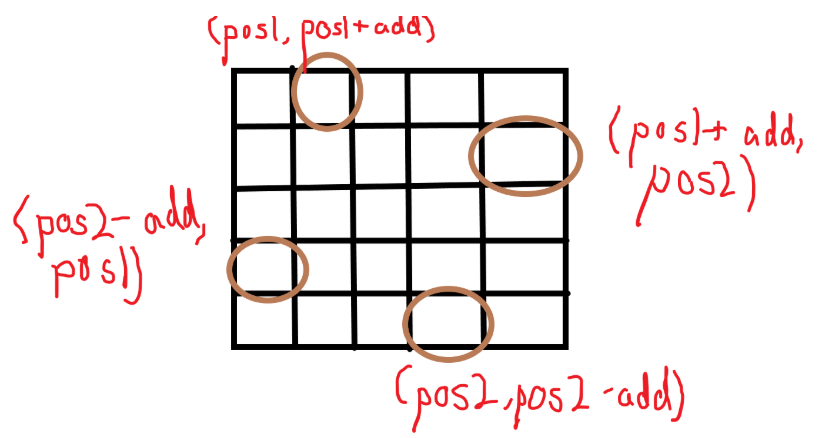
具体旋转4个点时:
可以先把第一个的点数据保存一下,然后第四个点放到第一个点,第三个点放到第四个点,第二个点放到第三个点,之前保存的第一个点放到第二个点
二维数组.length:行数
27
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。
示例:
输入: ["eat", "tea", "tan", "ate", "nat", "bat"]
输出:
[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]
说明:
- 所有输入均为小写字母。
- 不考虑答案输出的顺序。
public List<List<String>> groupAnagrams(String[] strs) { Map<String,List<String>> map = new HashMap<>(); for(int i=0;i<strs.length;i++){ char[] s= strs[i].toCharArray(); Arrays.sort(s); String key = String.valueOf(s); if (!map.containsKey(key)){ map.put(key,new ArrayList<>()); } map.get(key).add(strs[i]); } return new ArrayList<>(map.values()); }
29 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
解:
public int maxSubArray(int[] nums) { if(nums.length==0){ return 0; } int pre =nums[0]; int max = pre; int next; for(int i=1;i<nums.length;i++){ next = Math.max(nums[i],pre+nums[i]); max = Math.max(max,next); pre = next; } return max; }
语义 f( i ):以arr[ i ]为结尾的最长子串,该子串数字的总和。因此所有 f( i )的最大值就是题意所求。
索引: 0 ... i-2 i-1 i
数字: arr[ i-1] arr[ i ]
f( i )的可能子串1: arr[ i ]
f( i )的可能子串2: X X arr[ i ]
对于第二种情况,XX就是f( i-1 )对应的子串
所以:f ( i ) = max( f( i-1 )+arr[ i ] , arr[ i ] )
此处代码还采用滚动数组思想
30. 跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4] 输出: true 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4] 输出: false 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
解:
public boolean canJump(int[] nums) { int rightMax =0; for(int i=0;i<nums.length-1;i++){ if(i<=rightMax){ rightMax = Math.max(i+nums[i],rightMax); }else { // 即将要到达的i>最远能到的索引,后面就走不动了,直接得到最远值 break; } } // 用最远值和n-1比较 if(rightMax>=nums.length-1){ return true; }else { return false; } }
由于数组中的每个元素只是一个上限,所以可以先求出最远能到达的索引位置,若它>=n-1,则true,否则false
把最远能到达的索引作为公共变量
例如:
索引:0 1 2 3 4
数组:3 2 1 0 4
从0出发,最远达到的索引为3,由于1<3,所以可以到索引1,1+arr[ 1 ] = 1+2=3《=3,所以最远到的索引还是3;
然后走到2,2+arr[ 2 ] = 3<=3,所以还是最远还是3
然后到索引3,3+0<=3,依然最远3
此时后面还有元素,但是不能往后走了,因为最远是3
此时得到数组最远能到达3,由于3<n-1=4,所以返回false
31. 合并区间
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: intervals = [[1,3],[2,6],[8,10],[15,18]] 输出: [[1,6],[8,10],[15,18]] 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: intervals = [[1,4],[4,5]] 输出: [[1,5]] 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
提示:
intervals[i][0] <= intervals[i][1]
解:
public int[][] merge(int[][] intervals) { // 特殊情况 if(intervals.length==0){ return intervals; } // 二维数组排序,每一行是一个整体,按照每行的第一个元素排,小的在前 Arrays.sort(intervals, new Comparator<int[]>() { @Override public int compare(int[] ints, int[] t1) { return ints[0]-t1[0]; } }); // 结果集 List<int[]> res = new ArrayList<>(); int count = 0; // 结果集中的最后一个位置 for(int i=0;i<intervals.length;i++){ if(res.isEmpty()){ res.add(intervals[0]); }else { if(res.get(count)[1]<intervals[i][0]){ res.add(intervals[i]); count++; }else { res.get(count)[1]=Math.max(res.get(count)[1],intervals[i][1]); } } } // 将ArrayList转成二维数组 int[][] r = new int[res.size()][intervals[0].length]; for(int i=0;i<res.size();i++){ r[i]=res.get(i); } return r; }
二维数组排序,每一行是一个整体,按照每行的第一个元素排,小的在前
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] ints, int[] t1) {
return ints[0]-t1[0];
}
});
为了方便研究,先以每个区间的左端点为标准,升序排列区间
然后开始遍历所有区间,碰到第一个区间,先加到结果集中;
然后是第二个区间,如果该区间的左端点>结果集最后一个区间的右端点,则作为新区间加入结果集;
如果相反,说明可以与结果集的最后一个区间合并,最后一个区间的右端点 = max(最后区间的右端点, 新区间的右端点)
然后接着同样方法遍历到结尾
32
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?

例如,上图是一个7 x 3 的网格。有多少可能的路径?
示例 1:
输入: m = 3, n = 2 输出: 3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向右 -> 向下 2. 向右 -> 向下 -> 向右 3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3 输出: 28
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10 ^ 9
解:
public int uniquePaths(int m, int n) { int[][] d = new int[m][n]; for (int j=0;j<n;j++){ d[0][j]=1; } for (int i=0;i<m;i++){ d[i][0]=1; } for (int i=1;i<m;i++){ for (int j=1;j<n;j++){ d[i][j]=d[i-1][j]+d[i][j-1]; } } return d[m-1][n-1]; }
33
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入: [ [1,3,1], [1,5,1], [4,2,1] ] 输出: 7 解释: 因为路径 1→3→1→1→1 的总和最小。
解:
public int minPathSum(int[][] grid) { int m=grid.length; int n=grid[0].length; int[][] d = new int[m][n]; int sum=0; // 边界条件 for(int i=0;i<m;i++){ for(int j=i;j<m;j++){ d[i][n-1] += grid[j][n-1]; } } // 边界条件,此时右下角已经计算出,不用考虑右下角了 for(int j=0;j<n-1;j++){ for (int i=j;i<n;i++){ d[m-1][j]+=grid[m-1][i]; } } for(int i=m-2;i>=0;i--){ for (int j=n-2;j>=0;j--){ d[i][j] = grid[i][j] + Math.min(d[i][j+1],d[i+1][j]); } } return d[0][0]; }
34
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution" 输出:5 解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
解:
public int minDistance(String word1, String word2) { int[][] d = new int[word1.length()+1][word2.length()+1]; // 边界 for(int i=0;i<word1.length()+1;i++){ d[i][0]=i; } // 边界 for(int i=0;i<word2.length()+1;i++){ d[0][i]=i; } for (int i=1;i<word1.length()+1;i++){ for (int j=1;j<word2.length()+1;j++){ if(word1.charAt(i-1)==word2.charAt(j-1)){ d[i][j]=d[i-1][j-1]; }else { d[i][j]=1+Math.min( Math.min(d[i-1][j],d[i][j-1]) ,d[i-1][j-1] ); } } } return d[word1.length()][word2.length()]; }
d[ i ][ j ]:针对串a的前 i 个字符和串b的前 j 个字符,所需的最少操作数
是否分类讨论:
如果最后一个字符一样: d[ i ][ j ] = d[ i-1 ][ j-1 ]
如果最后一个字符不一样,则最后结果肯定是要让它们一样的:
如果第一步删除最后一个字符:d[ i ][ j ] = 1+d[ i-1 ][ j ]
如果第一步修改:d[ i ][ j ] = 1+d[ i-1 ][ j-1 ]
如果第一步补充:d[ i ][ j ] = 1+d[ i ][ j-1 ]
所以d[ i ][ j ] = min( 1+d[ i-1 ][ j ] ,1+d[ i-1 ][ j-1 ] ,1+d[ i ][ j-1 ] ) = 1 + min( d[ i-1 ][ j ] ,d[ i-1 ][ j-1 ] , d[ i ][ j-1 ] )
编程时,给每个字符串前面加上空串,即字符串的第0项是空,第一项是第一个字符;
可以采用循环来实现,也可以采用递归这个编程快,但是可能超时
35最小覆盖子串
给你一个字符串 S、一个字符串 T 。请你设计一种算法,可以在 O(n) 的时间复杂度内,从字符串 S 里面找出:包含 T 所有字符的最小子串。
示例:
输入:S = "ADOBECODEBANC", T = "ABC" 输出:"BANC"
提示:
- 如果 S 中不存这样的子串,则返回空字符串
""。 - 如果 S 中存在这样的子串,我们保证它是唯一的答案。
解答:
public String minWindow(String s, String t) { int needCnt=0; int[] res =new int[2]; // res[0]:合格字符串首字母索引,res[1]:合格字符串最后一个索引+1 res[1]=s.length()+1; // 初始化为一个j不可能达到的值,方便更新 Map<Character,Integer> need = new HashMap<>(); // 初始化need哈希表 for(int i=0;i<t.length();i++){ if(!need.containsKey(t.charAt(i))){ need.put(t.charAt(i),0); } Integer value = need.get(t.charAt(i))+1; need.put(t.charAt(i),value); needCnt++; } int j=0; // 指向下一个要访问的 for(int i=0;i<s.length();i++){ while(j<s.length()+1){ // 如果j指向末尾的后一个,还要再判断一次当前字符串是否合格,如果合格则更新,如果不合格就不必要处理第j项了,直接break if(needCnt==0){ if(j-i<res[1]-res[0]){ res[0]=i; res[1]=j; } break; } if(j==s.length()){ break; } if(!need.containsKey(s.charAt(j)) ){ need.put(s.charAt(j),0); } if( need.get(s.charAt(j))>0) { needCnt--; } Integer value = need.get(s.charAt(j))-1; need.put(s.charAt(j),value); j++; } Integer v = need.get(s.charAt(i))+1; need.put(s.charAt(i),v); if(v>0){ needCnt++; } } // 如果就没更新,说明找不到合格子串 if(res[1]==s.length()+1){ return ""; }else{ return s.substring(res[0],res[1]); } }
从一个字符开始找到刚好能包含目标串的所有字符的子串,合格字符串就在所有这些子串之中,因此从头往后遍历每个字符。下面结合图具体操作:
用字符串T初始化need哈希表:表示此时缺1个A,1个B,1个C,need当中>0的才是所需要的元素。needCnt:缺T中的字符总共多少个

上图说明:
i初始化为0,表示先看第0个字符,j指向0,i和j确定一个字符串,此时看need[s[j]]==need['D'],若有D则减一,若无则哈希表注册上D,并且减一
由于D不是T里面的字符,即need['D']<=0,因此不用管needCnt。
由于needCnt!=0,说明还需要字符,此时继续往后遍历‘O’,同理;
到A时,由于need[s[i]]==need['A']>0,说明是需要的元素,此时need[s[i]]和needCnt都要-1
由于needCnt==2!=0,继续往后遍历到C为止,此时得到D到C的字符串,是包含T的且j不能再往后走了(保证最小),此时把i,j都更新到res结果数组中,作为初始的最短子串
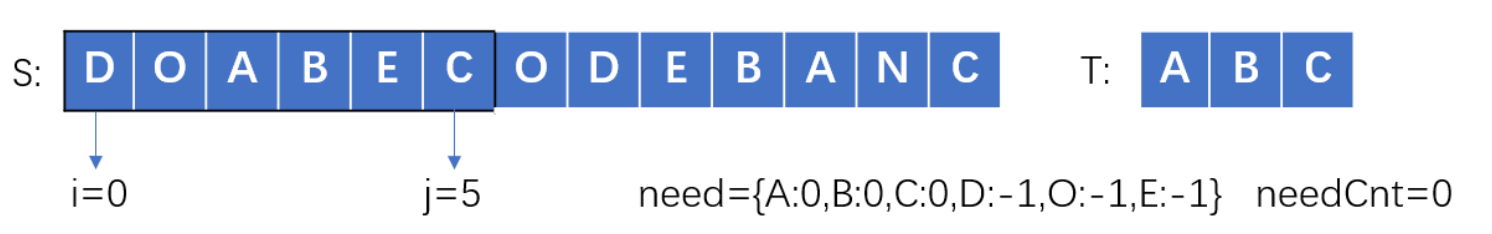
上图说明:
接下来i往后走,看以第1个字符开头的,need['D']要+1,由于D不是T里面的字符,即need['D']<=0,就不用动needCnt,j不需要动,因为小于j的子串一定不符合,否则j就到不了那里。
由于needCnt==0,该子串符合条件,
此时need={A:0,B:0,C:0,D:0,O:-1;E:-1}

上图说明:
i继续后走,need['O']+1,由于needCnt==0,依然符合条件

i往后走,need['A']+1,由于此时need['A']>0了,即需要的字符被取走了,所以needCnt++,由于needCnt!=0,所以j往后走...
最后直到 i 都数完了,此时每次得到一个合格子串就和最小的比较一下,就得到最短的子串了。
36子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
解:
public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res = new ArrayList<>(); if(nums.length==0){ // 如果数组为空,则返回:[[]] res.add(new ArrayList<>()); return res; } int[] prenums = new int[nums.length-1]; System.arraycopy(nums,0,prenums,0,nums.length-1); List<List<Integer>> pre = subsets(prenums); for(int i=0;i<pre.size();i++){ res.add(new ArrayList<>(pre.get(i))); pre.get(i).add(nums[nums.length-1]); res.add(new ArrayList<>(pre.get(i))); } return res; }
b = new ArrayList<>(a); // b和a的地址不同,但是b和a里面的元素一样,对a添加或删除不用影响b
但是如果a里面元素是对象,如list,那么对a里面的元素做改动。就会影响到b
List b = a;// 对a怎么操作,b会同样影响
f(num):基于该数组返回合法的结果
f(num) = f(num从0到倒数第二项) U ( num的最后一项合入到 f(num从0到倒数第二项) 的每一项中 )
38 单词搜索
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board = [ ['A','B','C','E'], ['S','F','C','S'], ['A','D','E','E'] ] 给定 word = "ABCCED", 返回 true 给定 word = "SEE", 返回 true 给定 word = "ABCB", 返回 false
提示:
board和word中只包含大写和小写英文字母。1 <= board.length <= 2001 <= board[i].length <= 2001 <= word.length <= 10^3
解:
public boolean exist(char[][] board, String word) { if(board.length==0){ return false; } // 记录当前位置是否访问过 boolean[][] status = new boolean[board.length][board[0].length]; // 每行代表一个偏移方向 int[][] direction = {{1,0},{0,1},{-1,0},{0,-1}}; // 遍历所有格子,若有一个满足,则OK for(int i=0;i<board.length;i++){ for (int j=0;j<board[0].length;j++){ if(dfs(i,j,board,word,status,direction,0)){ return true; } } } return false; } public boolean dfs(int i,int j,char[][] board,String word,boolean[][] status,int[][] direction,int start){ if(start+1 == word.length()){ return board[i][j]==word.charAt(start); } if(board[i][j]!=word.charAt(start)){ return false; } status[i][j]=true; for(int k=0;k<4;k++){ int ii =i + direction[k][0]; int jj =j + direction[k][1]; if(ii>=0 && ii<board.length && jj>=0 && jj<board[0].length && status[ii][jj]==false){ if(dfs(ii,jj,board,word,status,direction,start+1)){ return true; } } } // 从当前格子出发后,发现四周都不行了,接下来回退上一步,由于后期又能访问它,则恢复false status[i][j]=false; return false; }
搜索以第(0,0)个字符打头是否有匹配的,如果没有,则搜索以第(0,1)个...直到发现则返回true,否则遍历所有格子看看
方法一:
语义:f(i,j,k) :搜索以第(i,j)打头的字符是否有和word的【k:n-1】匹配的
f(i,j,k) = board[ i ][ j ] == word[ k ] &&
(
(i-1,j)在区域内 && f(i-1,j,k+1) ||
(i+1,j)在区域内 && f(i+1,j,k+1) ||
(i, j-1) 在区域内 && f(i,j-1,k+1) ||
(i,j+1)在区域内 && f(i,j+1,k+1)
)
边界不好定,则换方法
方法二:基于dfs
从根节点出发(到当前字符这里),看是否符合判断条件(是否和word的第0个字符匹配,若不匹配,则直接false)
若符合要求(匹配),则当前位置标上true,表示已经访问过了,下次不要再访问
然后继续遍历下一个可以访问的节点(上下左右去遍历,而且上下左右不能出到区域外面,如先上走一步,即 i=i-1,j=j+0)
dfs(新的节点) ( 新 i,j 确定新的节点,再传入新的判断条件:能和word的第1个字符匹配, 如果返回true,则表示后面的都没问题,也返回true )
递归出口:看是否只剩1个字符了,就直接将它和board[ i ][ j ]比较
总方法中,遍历完该节点后,状态变量被污染,需要重新置为false
39
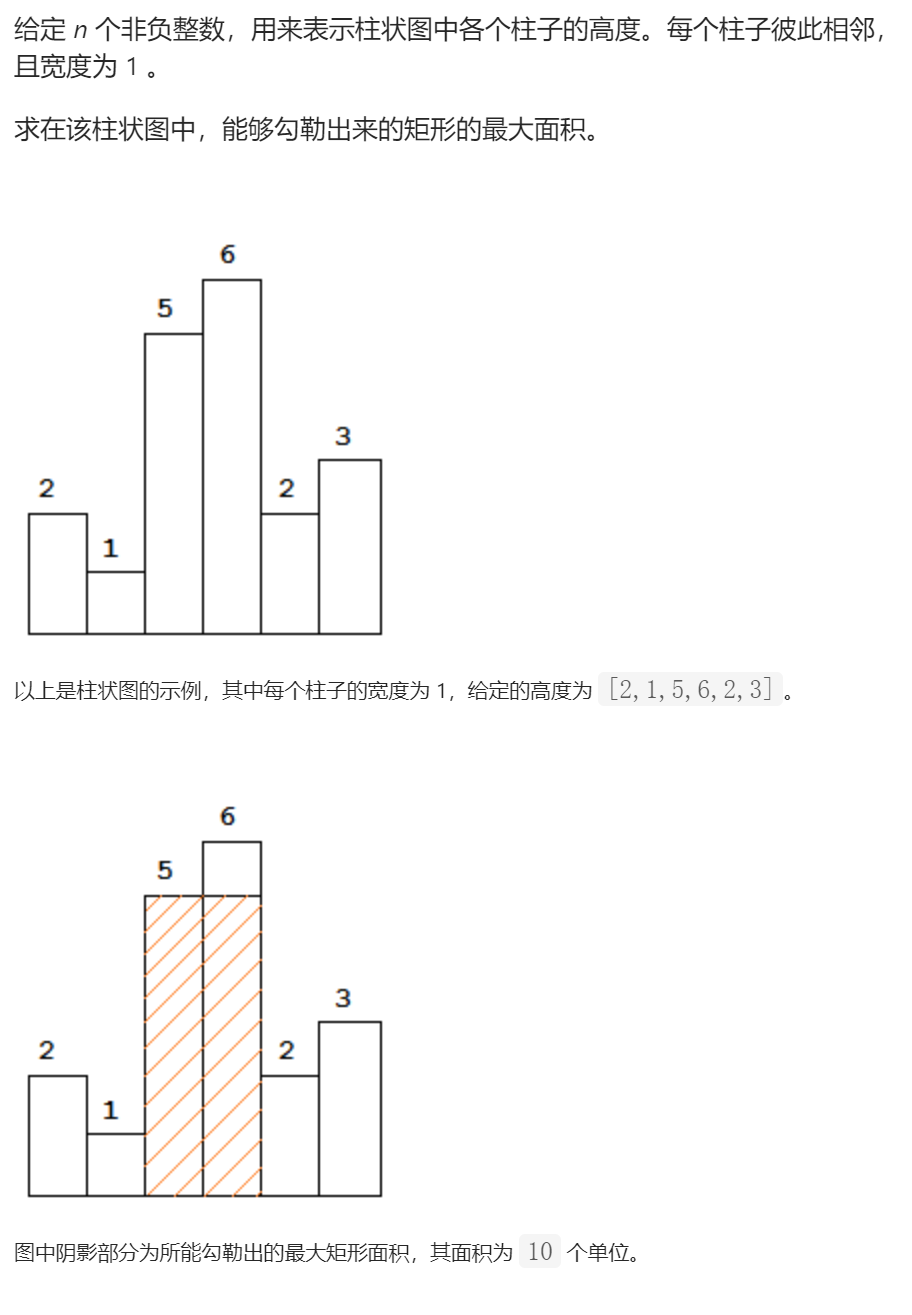
示例:
输入: [2,1,5,6,2,3] 输出: 10
解:
public int largestRectangleArea(int[] heights) { int max =0; // 为了统一化管理,给两边多加-1元素 int[] newHeight = new int[heights.length+2]; newHeight[0]=-1; newHeight[newHeight.length-1]=-1; System.arraycopy(heights,0,newHeight,1,heights.length); int left; int right; for(int i=1;i<newHeight.length-1;i++){ left = i; right = i; while (newHeight[left-1]>=newHeight[i]){ left--; } while (newHeight[right+1]>=newHeight[i]){ right++; } int cur = (right-left+1) *newHeight[i]; max = Math.max(max,cur); } return max; }
把问题分解到每个柱子身上,每个柱子都对应一个它自己的最大矩形,那么符合要求的矩形就在这里面
怎么找每个柱子对应的矩形:是建立左右指针,让2个指针尽可能的远
左指针向左延伸直到发现第一个比它高度小的柱子停止,右指针向右延伸直到找到第一个比它高度小的停止
2个指针之间的差就是矩形的宽度
40
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入: [ ["1","0","1","0","0"], ["1","0","1","1","1"], ["1","1","1","1","1"], ["1","0","0","1","0"] ] 输出: 6
解:
获得输入:
Scanner input = new Scanner(System.in);
int a = input.nextInt(); // 整数
解:
public int maximalRectangle(char[][] matrix) { if(matrix.length==0){ return 0; } int max = 0; int[] heights = new int[matrix[0].length]; for(int i=0;i<matrix.length;i++){ for(int j=0;j<matrix[0].length;j++){ if(matrix[i][j]=='0'){ heights[j]=0; }else { heights[j]+=1; } } // 每求出一行的最大矩形,就和最大值比较一下 max = Math.max(largestRectangleArea(heights),max); } return max; } public int largestRectangleArea(int[] heights) { int max =0; // 为了统一化管理,给两边多加-1元素 int[] newHeight = new int[heights.length+2]; newHeight[0]=-1; newHeight[newHeight.length-1]=-1; System.arraycopy(heights,0,newHeight,1,heights.length); int left; int right; for(int i=1;i<newHeight.length-1;i++){ left = i; right = i; while (newHeight[left-1]>=newHeight[i]){ left--; } while (newHeight[right+1]>=newHeight[i]){ right++; } int cur = (right-left+1) *newHeight[i]; max = Math.max(max,cur); } return max; }
拼凑最大矩形可以联想到之前上一道求柱状图中的最大矩形,但是此处的矩形是飘忽不定的,因此转化到此题:
如何让矩形降下来呢?让矩形的每一行都有可能成为最后答案的底,因此遍历矩形的每一行,并且以每一行为底边
当以某行为底边时,若该行的某一列有0出现,则答案一定不会和该列有染,所以可以假定该列的柱子高度是0,若是1,则多少个连续的1就是该柱子的高度:
假定以第2行为底边:
1 0 0
0 1 1
1 1 0
第一个柱子高度是1,第二个是2,第三个是0,此时求出最大的矩形(仅代表该行的),同理往下求



 浙公网安备 33010602011771号
浙公网安备 33010602011771号