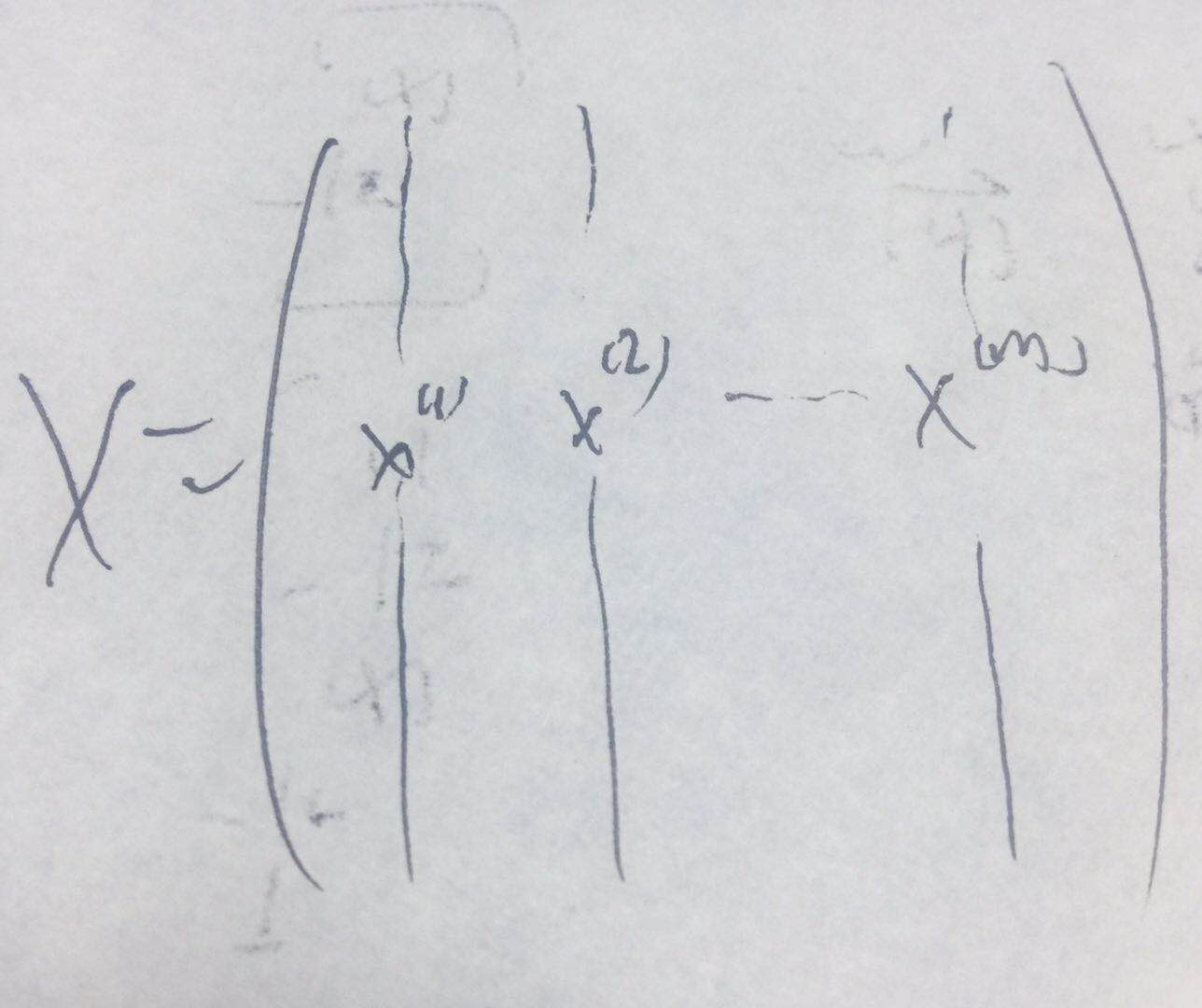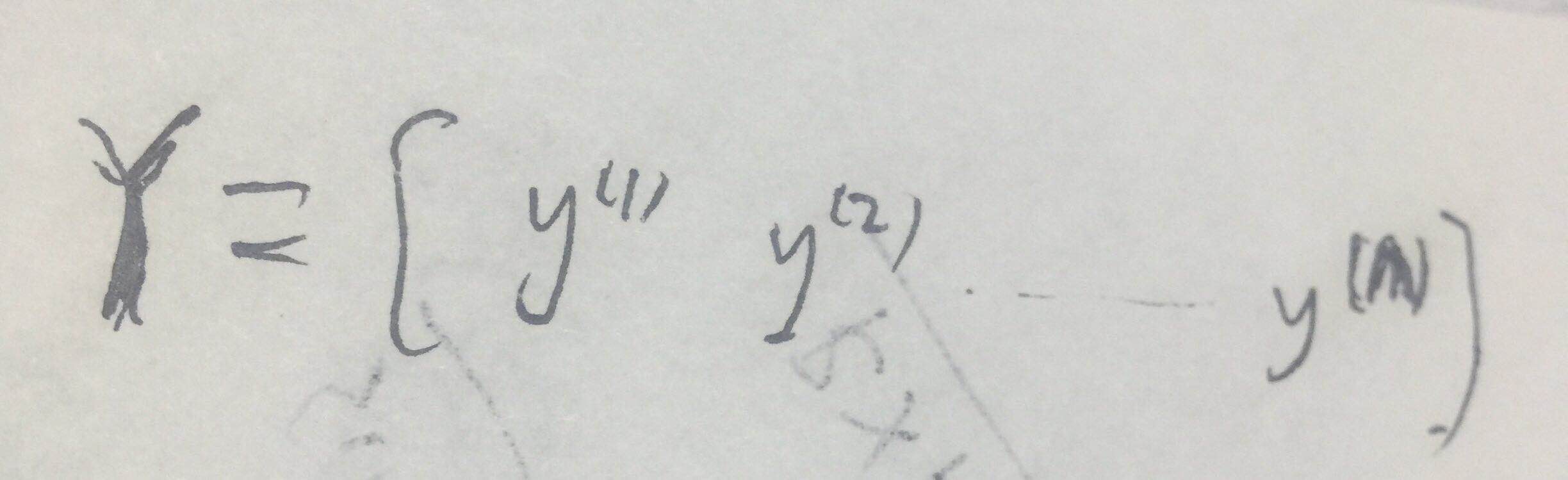逻辑回归

 

1.定义

逻辑回归属于一种分类算法，因变量为分类变量。

2.假设函数

通常令假设函数（此处为一个非线性假设）为（无非就是套在了激励函数里面了）：

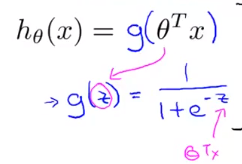
其中该假设函数的输出结果为：y=1的概率值

等价的，可以用新符号来表示，将拦截项专门拿出来，此时参数和x都没有1这一项了：

 

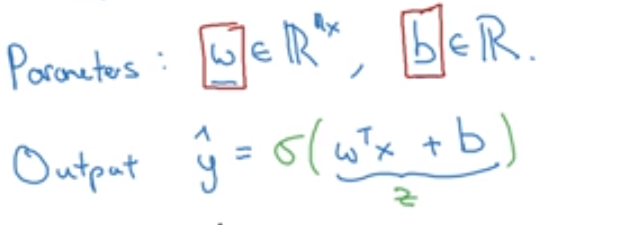
3.决策边界（decision boundary）

它是假设函数的一个属性，令通过决策边界可以直观的看出，若样本在什么位置，就能预测出这个样本对应的预测值是多少了。

若h(x) = sigmoid( -3 + x1 +x2 ) , 且当h(x)>0.5时，就做出决策y=1,反之。

则：-3 + x1 +x2 > 0 ，则 y =1 ,反之。因此 -3 + x1 +x2 = 0是h(x)的决策边界。对应的图为：

在逻辑回归问题当中，若特征有2种，采用二次多项式进行拟合：

则设定假设函数（其中g(x) = sigmoid(x) ）：

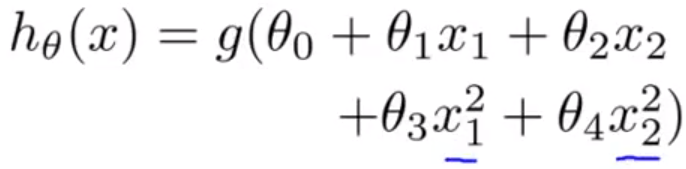
注意：计算时，就把x1转为原来的x1,x2...x2,x1^2转为x3,x^2转为x4，然后按之前的线性假设函数算就好了。即把非线性拟合转为线性拟合问题。

 

 假定已经知道了参数（本来是求出来的）：

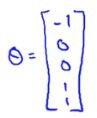
则有：

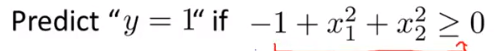
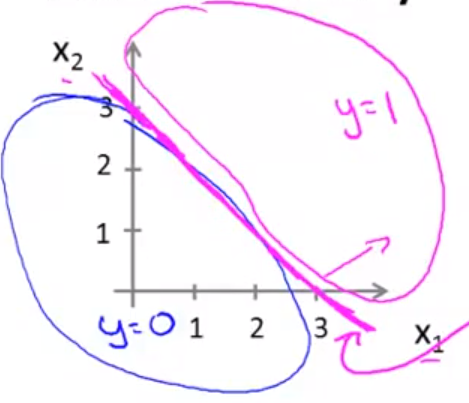
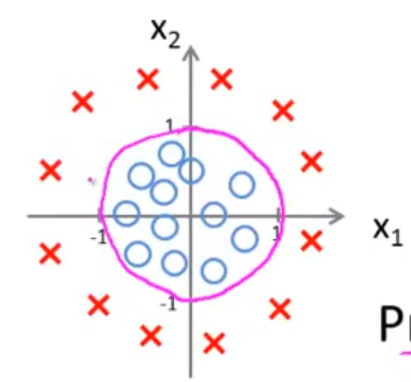
则 x1^2 + x2^2 = 1 是h(x)的决策边界，见下图：

 

 4、代价函数（无正则项的）

此时用交叉熵代价函数而不用均方误差代价函数的原因：

当h(x) = sigmoid (θ’*x)时，代价函数是非凸函数，例如：

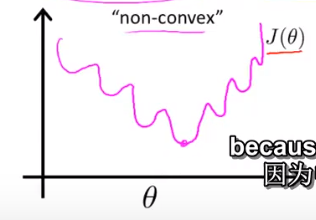
这里有很多局部最优解，会导致梯度下架算法无法收敛到全局最优。

交叉熵代价函数会很好地避开这一点，且它的物理意义符合预期，即若标签值y为1，则h(x) =0 的代价就很大，反之。

 若 y = 0 or 1 ,则定义交叉熵代价函数如下：

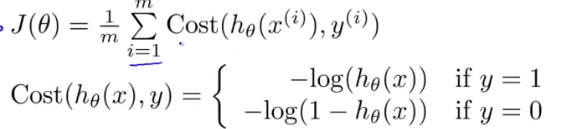
 等价于：

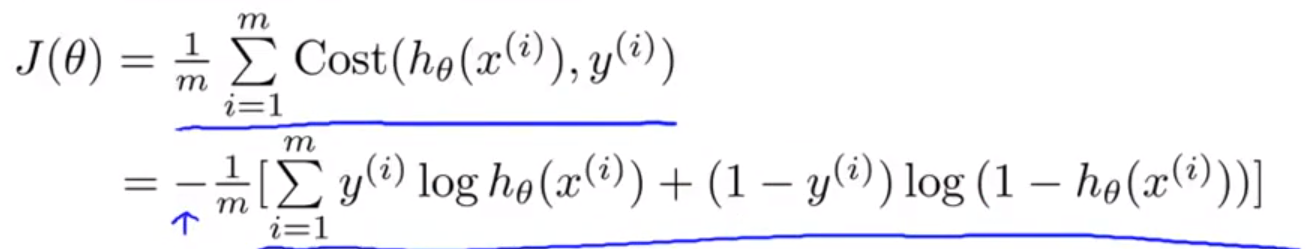
此代价函数等价的矩阵表示：

 

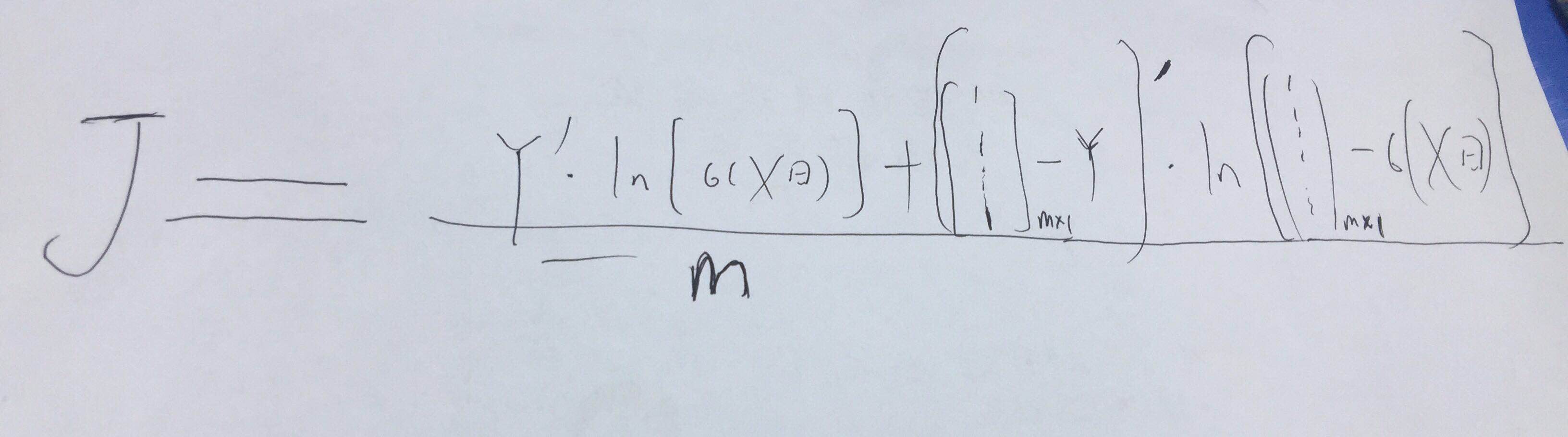
5、更新参数θ（无正则项的）

逻辑回归的梯度下降法公式：

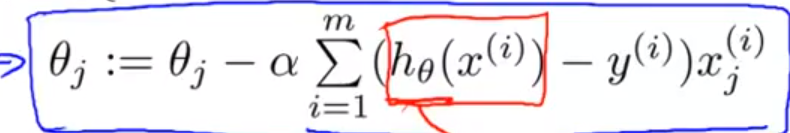
其等价的矩阵形式只需要稍微修改一下线性回归的假设函数即可。

证明：

  

=》

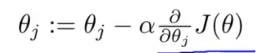
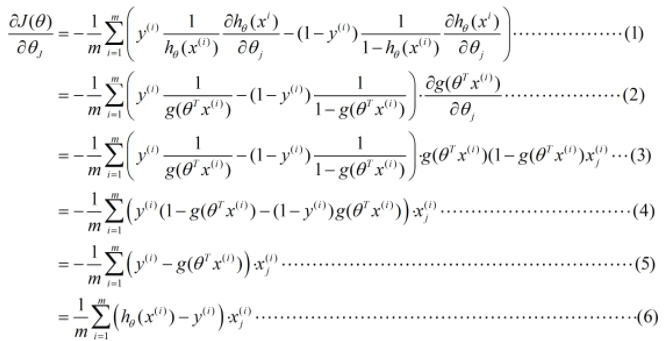
证闭。

更换符号的等价表示：（对下图的计算要迭代很多次，再加个for循环）

其中：计算Z的第一式子的b:

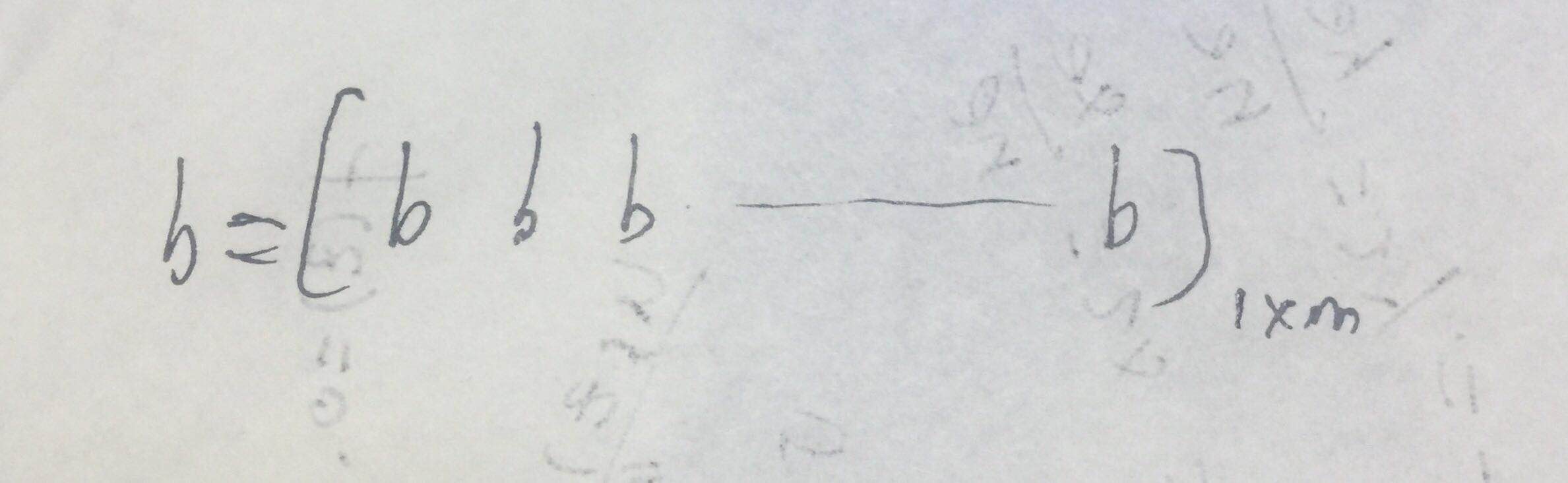
计算Z的第二式子的b是一个实数，但python会把这个实数广播为上图的形式。