梯度下降法
批处理梯度下降算法(batch gradient descent)
原理:初始化参数,然后拿到全部样本,根据全部样本算出代价函数对参数的偏导数,然后同时更新这些参数。接着还是全部样本,计算。。。。。
注意:要做同步更新参数,而不是先更新一个再更新另一个。

注意:如果如果学习率很大,则每一步都会迈得很大,最后可能不会收敛了,若学习率很小,则步子很小,收敛太慢。
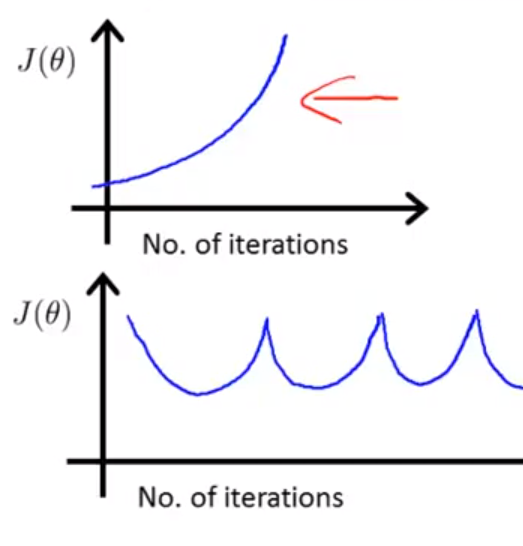
若学习率很大:(下图是y=J(θ)曲线,纵坐标为y)
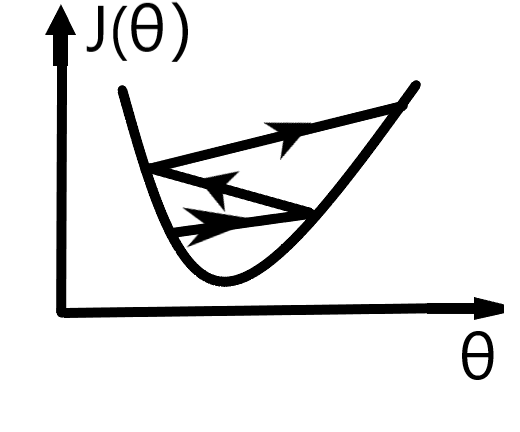
若学习率较小:
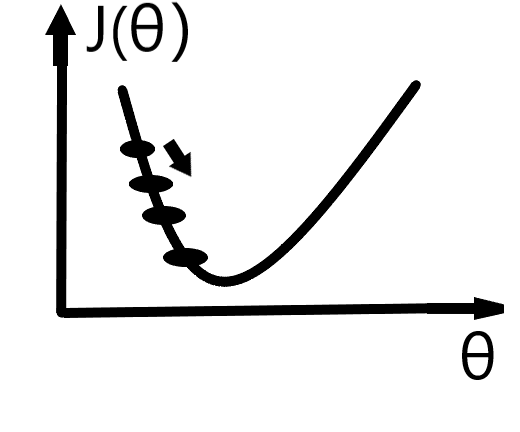
当采用均方误差形式的代价函数且为多元线性回归问题时,梯度下降算法表现为:

等价对应的矩阵表示:
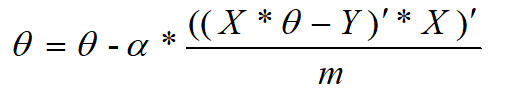
注意:若多元线性回归当中的不同特征值(或不同属性)的所处范围相差很大时,可以让对应属性上的每个元素 - 所有样本在该属性上的均值 / 这个属性的范围或者标准差 ,这样就将所有的特征值(属性值)映射到相同区间了,结果这批新数据的均值就为0,标准差为1,这样会加速梯度下降算法的收敛速度(feature scaling)。例如:
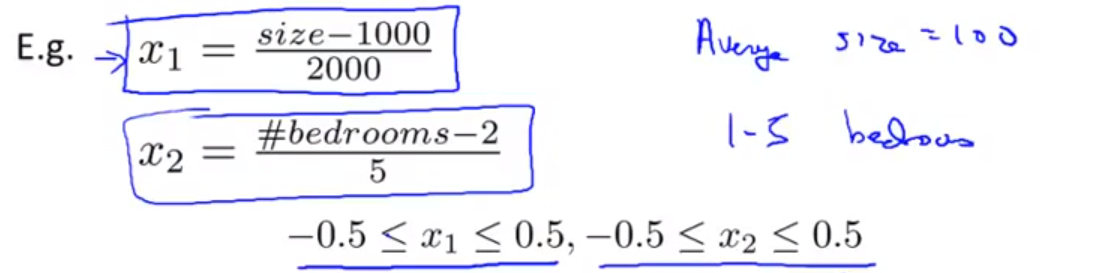
运行时,随着迭代次数的不断增加,参数也在不断地变化,(每迭代一次,参数变化一次),因而代价函数也在不断地变化。
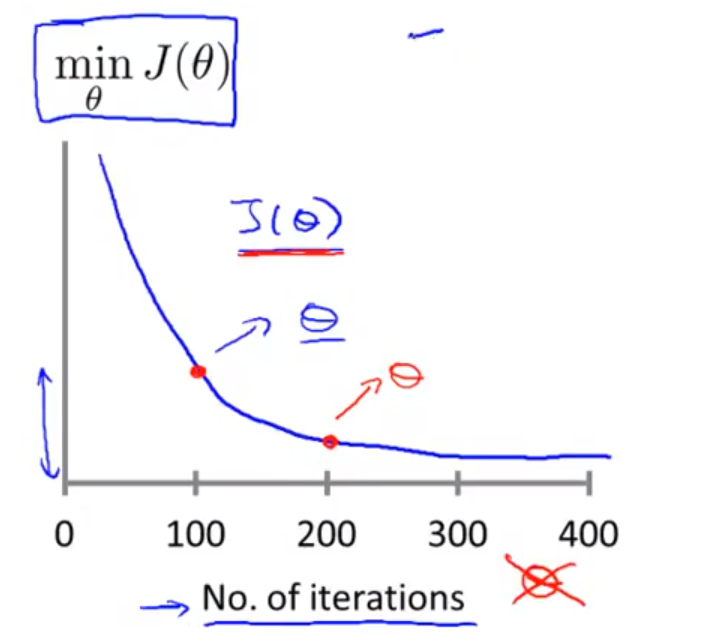
注意:当出现下面这些情况时,应该把学习率调低点:
一般这样尝试学习率:

随机梯度下降算法
一般如果样本数太大,2亿多个,或者在线的网站总有连续的用户流就用这招。寻找全局最小值的道路虽然是迂回的,但是总体上是对的。
定义:
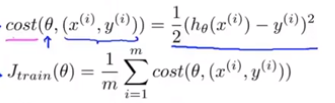
步骤(注意偏导数有变化,外层也可以循环上1到10次):

小技巧:为了更好地实现算法的收敛,可以使得学习率动态变化:
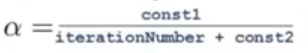
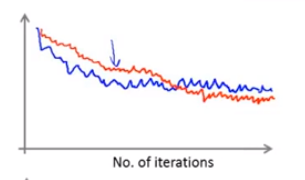
算法 评价方法:每1000次迭代算一下cost值(更新θ之前),该cost值是前1000个样本的cost的平均值,随后把图画出来看看。比如下图,红色代表学习率更小的那一条,波动表示存在噪声。当然,若每5000次算一下,那么曲线会更平滑一点。
mini-batch gradient descent
它是前2者的折中,第一次选b个样本进行训练,第二次选新的b个样本进行训练。。。。




