The Math

一个圆锥可以被描述在一系列方式上，但是我选择如下的参数作为输入。

  • d：轴，被定义，作为一个标准向量，从base到apex。
  • a：apex的位置。
  • h：cone的高度
  • rd：准线的半径。
  • n：径向切片的数量。

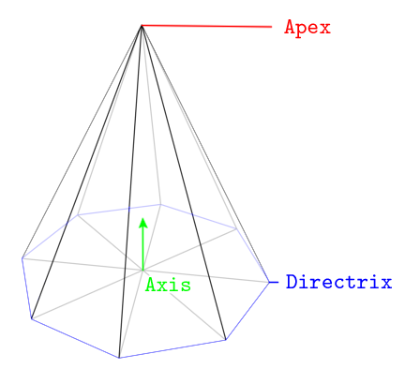
image

圆锥由两个三角形扇组成，首先从顶点出发，其次，从基本质心发出。
两个都由一个n个点的离散集合，从准线采样获取。主要的困难是计算这些采样的点。
一个通用的方式对于这种类型的问题是，依据不同的坐标系系统，允许更多的自然的表达式。当解决一个圈在一个平面的时候，球极坐标系是一个很好的下注，我们可以制定每个点作为一个元组$$(\theta, r)\in R^2$$，然后影视这些值到3D世界坐标，使用一个球极到直角坐标系的转换。

点的初始计算是相当直接的。在一个循环里面，索引$$i\in N$$范围，来自于0，1...，n，每个连续点的极角$$\theta$$通过$$2i\pi/n$$给出，并且半径总是参数$$r_{d}$$。为了转换这些值，我们将从传统的形式开始，$$x = rcos\theta, y = rsin\theta$$，在一个新的方式。特别的，让我们把平面嵌入进去，把计算看作是标准基向量的线性组合，i，j和k：$$(x, y, z) = rcos\theta i + rsin\theta j + ok$$。在我们可以应用这个变换之前，我们纠正旋转和位置。

旋转，可以被解释，通过交换i，j，k，对于一组新的基向量，对齐到圆锥的基平面，而不是x，y平面，通过改变基向量。我们将开始通过定义$$e_{2} = d$$作为我们新的k，因为它类似于基平面的法线。在我的应用，圆锥如何绕轴旋转不重要，那么，我唯一的请求，对于新的基准，就是另外两个向量位于基平面的某处。因此，我定义了一个抽象函数perp(v)，返回一个向量，位于某处，在平面，垂直于v，并且使用这个函数去生成一个第二个向量$$e_{0} = perp(e_{2})$$，可以被视为i。最后一个向量$$e_{1}$$是由e2和e0的叉积组成，并且对应于j。

在解决位置之前，对最终的位置机能与数学的关系进行评论是合适的。自从OpenGL默认，剔除多边形，被描述在顺时针(CW)方法，我们想去列出两个三角面的顶点，逆时针(CCW)相对于观察者。我们计算$$e_{1} = e_{2}\times e_{0}$$的方式，将替换$$e{1}$$ 90度，从$$e_{0}$$逆时针的方向，当从半空间定位观察的时候，通过$$e_{2}$$。这意味着，我们可以直接地绘制圆锥的顶部，但是，我们将去以某种方式逆转顶点的顺序，当我们绘制基座的时候。

最后一个变换就是统计位置。这个可以轻松地被完成，通过添加base centroid，
c = a + (-dh)，对于表达式，我们总结出：

\[(x, y, z) = c + rcos\theta e_{0} + rsin\theta e_{1} + 0e_{2} = c + [((e_{0}cos\theta) + (e_{1}sin\theta))r]。\]

perp(v)的具体实现：

Vector3f perp(const Vector3f &v) {
    float min = fabsf(v.x());
    Vector3f cardinalAxis(1, 0, 0);

    if (fabsf(v.y()) < min) {
        min = fabsf(v.y());
        cardinalAxis = Vector3f(0, 1, 0);
    }

    if (fabsf(v.z()) < min) {
        cardinalAxis = Vector3f(0, 0, 1);
    }

    return CrossProduct(v, cardinalAxis);
}

圆锥绘制函数：

void drawCone(const Vector3f &d, const Vector3f &a,
              const float h, const float rd, const int n) {
    Vector3f c = a + (-d * h);
    Vector3f e0 = perp(d);
    Vector3f e1 = CrossProduct(e0, d);
    float angInc = 360.0 / n * M_PI_DIV180;

    // calculate points around directrix
    std::vector<Vector3f> pts;
    for (int i = 0; i < n; ++i) {
        float rad = angInc * i;
        Vector3f p = c + (((e0 * cos(rad)) + (e1 * sin(rad))) * rd);
        pts.push_back(p);
    }

    // draw cone top
    glBegin(GL_TRIANGLE_FAN);
    glVertex3f(a.x(), a.y(), a.z());
    for (int i = 0; i < n; ++i) {
        glVertex3f(pts[i].x(), pts[i].y(), pts[i].z());
    }
    glEnd();

    // draw cone bottom
    glBegin(GL_TRIANGLE_FAN);
    glVertex3f(c.x(), c.y(), c.z());
    for (int i = n-1; i >= 0; --i) {
        glVertex3f(pts[i].x(), pts[i].y(), pts[i].z());
    }
    glEnd();
}